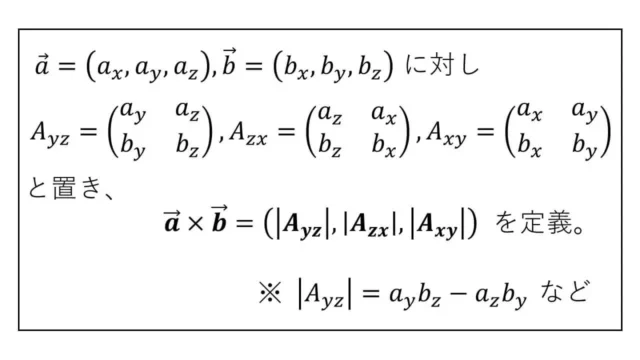大学数学 サイト 記事一覧のマップ【iwai-math-blog】

岩井の数学ブログ (iwai-math-blog) の サイトマップ になります。大学数学カテゴリーの各ブログ記事へのリンクを設置しています。
当サイトで、場所に迷うときには、こちらから再び一覧をご覧頂けます。また、全体を見て、必要なブログへお越し頂くことができます。
※ 高校数学についてのブログ記事は、高校数学の記事一覧に全てまとめています。
※ 一般教養の数学の目次という記事で、一般教養の数学のカテゴリーの記事たちへのリンクをまとめています。
【項目の順】
1. 基礎分野 2. 線形代数学 3. 微分積分学
4. 代数学(環・体・群・加群)
このページの上から下へ、この順で記事を配置しています。
青色の文字を押すと、リンク先の記事へ移動します。
大学数学 サイト :記事一覧【基礎分野】
まず、大学数学の全般で使う基礎となる内容の記事たちです。論理規則、集合、写像の対応についての内容が中心になります。
【大学数学の基礎内容】
・一意の証明(代数閉包の一意性も)
・直積集合(二項演算へ)
・全単射(必要十分条件)
・結合律(一般の結合法則)
・分配律(一般の分配法則)
・論理記号(集合と∀∃)
・同値関係(図も使って)
・組合せ(公式の証明)
・選択公理(集合族という写像から)
・超限帰納法(数学的帰納法の一般化)
高校の数学で学習した内容とともに、これらの内容が基礎となります。そこへ、線形代数学や微分積分学の理論が加わってくると、専門課程の理解へ向けてのしっかりとした土台になります。
また、変数に代入する値の範囲を論理的に考察するシグマ計算の練習として、メビウスの反転公式の証明は良いトレーニングになるかと思います。
ちなみに、最新の投稿です。
これらの最新の投稿は、新しく記事を投稿する毎に更新されます。
大学の内容を学習するにあたって、高校の数学を例として利用すると、理解しやすいかと思います。
・要素(元)
・和集合 共通部分
・補集合(ド・モルガン)
・命題-仮定-結論
高校では難しかった内容でも、大学の数学を学習していると、良い経験になるかと思います。
大学数学 サイト :線形代数学
【線形代数学の全般】
・線型空間の公理(定義)
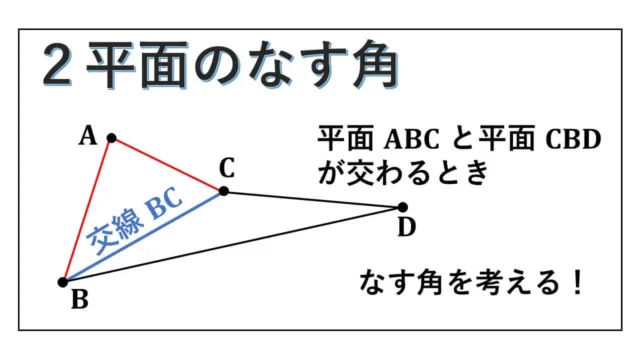
・外積
・不変部分空間(線形部分空間から)
・End(V)(線形変換の成す環)
・Reflection 鏡映変換
・表現行列(線形変換の行列表示)
・基底変換行列
・退化次数(nullの求め方)
・ツォルンの補題(無限次元で基底の存在)
・無限次元ベクトル空間(実数列)
・和空間の次元(W+W’)
・直和空間(W⊕W’)
・直交補空間(W⊥)
・商空間(線形代数で剰余)
・双対空間
・双対基底(dual basis)
線形代数学については、ベクトル空間論・行列論・固有値論という大きな三つの領域があります。
これらの各論点になる内容を記事で述べています。
<線形変換の行列表示と線形独立の観点>
また、微分作用素を行列で表示するということも記事にしています。
d/dx が線形変換として働くように、単純なベクトル空間を設定して、行列として表すことについて解説をしています。
さらに、内積の定義という記事で正規直交基底の作り方を解説しています。与えられた基底から大きさが 1 で互いに直交しているベクトルたちから成る基底を新しく作る方法になります。
【行列論&固有値論】
・trace(トレース)
・ブロック分割
・解の自由度(ランク)
・対角化(対角行列)
ベクトル空間の公理から、集合や写像の基本事項を適切に運用していくことで、それぞれの各論を押さえていくことが大切かと考えています。そうすることで、環論や加群などへと今後の理解の広がりが期待できます。
大学数学 サイト :微分積分学
【微積の基礎】
・max-min(最大値 最小値)の定義や表記
・デデキント切断(実数の連続性の公理)
・イプシロンデルタ論法(イプシロンエヌ法)
・はさみうちの定理(証明)
・二重数列(極限操作の順序)
・距離関数 (三角不等式)
・有界な単調数列(収束の証明)
・実数乗(指数が実数)
・偏微分可能(2変数関数の連続も)
・2変数関数の連続性(f(x, y) = xy)
・ノルム(norm)
・連続関数(有界閉集合上で定義されると最大値・最小値をもつ)
この過程で、近傍・集積点・開集合・閉集合を使いつつ、それらに慣れていけるように記事を書いています。この有界閉集合における最大値および最小値の存在を用いて、代数学の基本定理を証明しています。
複素数を通じて、代数学と解析学に触れるのも良いかと思います。
複素関数論
・複素指数関数(オイラーの公式)
・加法定理(複素三角関数で)
・主値【多価関数/複素対数関数】
指数関数について成立する指数法則も使いながら、オイラーの公式を使いつつ、複素対数関数を学習する流れになっています。
大学数学 サイト :代数学入門

【初等整数論入門】
高校の数学でも、整数の内容を学習しているので、そこを足掛かりにして学習を進めると良いかと思います。
まず、高校で触れた内容の延長としての初等整数論の内容たちです。
・余り-整数問題
・合同方程式の解き方
・中国剰余定理
・最大公約数-求め方
・フェルマーの小定理
・オイラーのファイ関数
これらの内容で、整数環 Z と剰余環 Z/nZ が活躍しています。
さらに、環論の一般的な理論へと理解を進めると良いかと思います。
可換環論入門
・ユークリッド整域(除法の定理の証明と整列集合)
・合同式の性質(剰余環Z/nZ)
・互除法(多項式でも)
・一次不定方程式(単項イデアル整域)
・イデアルの積(リー環も)
・環準同型写像(単射mono)
・極大イデアル (素イデアル)
・素元-既約元
・一意分解整域(素元分解整域)
・ネーター環(定義)
inclusion 埋め込みという記事で、同型な構造を埋め込むことについて述べています。
さらに、可換体論への準備となる理論たちです。
可換体論入門
【多項式環から】
・円分多項式が整数係数の多項式
・重根【多項式環の形式的な微分】
三次方程式の重根については、判別式を用いての考察しています。
【可換体論の入門内容】
・有限体の標数(ある素数で、位数はその素数のベキ)
・有限体の乗法群(巡回群)
・完全体(分離的とは)
・ガロア群
つづいて群論になります。
群論入門
・群の公理(逆元が唯一)
・部分群の判定方法(中心や正規化群を例に)
・ラグランジュの定理
・二面体群(二元生成)
・第二同型定理
・一般線形群(中心を求める)
・自己同型写像(Aut(G))
・共役類 類等式(共役作用)
・クラインの四元群(乗積表を作る)
・軌道分解(A4の共役作用)
・p群の中心(自明でない)
・外直積と内直積(正規部分群も関連)
・群拡大(群の短完全列)
・交換子群(交換子群列)
・可解群(位数2023の群は可解)
・n次交代群(n≧5だと単純)
・群の作用(4次対称群は可解)
・二重可移(置換群)
・べき零群(降中心列と昇中心列)
また、群の作用に関連して、軌道の位数についての考え方から、
シローの定理という有限群を学習するときに基本となる大切な定理が証明できます。
ここまでの理解を使って、有限生成アーベル群の構造を決定することができます。
・自由アーベル群
・ねじれ群
・有限生成アーベル群の基本定理
線形代数学を勉強するときに、行列式の定義に対称群(置換群)が使われます。対称群といったり、置換群といったりしますが、これは異なる n 個のものを入れ替える操作を集めてできる群です。
この入れ替え操作から行列式に関わる対称群に慣れるための記事が次です。
大学で扱う数学は抽象的で難しものが多いので、高校の数学から徐々に連結するように学習を進めていくと良いかと思います。
加群入門
加群について、剰余加群と自由加群を理解すると、加群のテンソル積への道が拓けます。
・加群の定義(部分加群と剰余加群)
・自由加群(形式的な有限和)
・不定元 x(多項式環へ)
・テンソル積(普遍性も)
各記事が数学の理解のお役に立てれば、幸いです。