シローの定理 | シローp部分群は存在し、互いに共役で、個数は1+pkという形

2022年12月16日

シローの定理 (Sylow) は、次の四つです。群Gの位数を割り切る素数 p の最高ベキが p の n 乗のとき、位数が p の n 乗である部分群が存在するという存在証明。

そして、G の p-部分群はシローp-部分群に含まれるということと、シローp-部分群は互いに共役であるということ。

さらに、シローp-部分群の個数についての定理もあります。

この記事では、これら四つの命題の証明を解説しています。

素数 p が絡むので、まずは高校数学の考え方で示すことができる補題から説明します。

シローの定理 :まず準備となる補題

【補題1】

p を素数、n を自然数とする。r は 0 以上の整数とする。
q = pⁿr とすると、_qC_pⁿ と r は p の同じベキで割り切れる。

＜証明＞

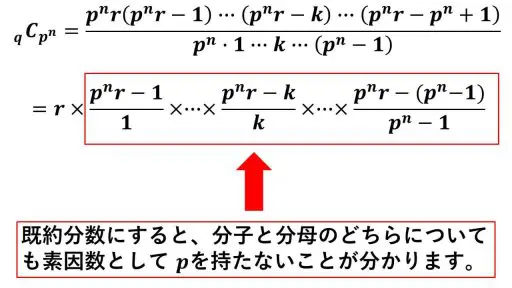
赤色の枠で囲っている部分は、既約分数にすると、分子と分母のどちらも p を素因子として持たないことが分かります。

そのため、_qC_pⁿ と r は p の同じベキで割り切れるということになります。

※ 組合せの公式については、リンク先のブログ記事で解説をしています。

赤色の枠で囲っている部分が、既約分数にすると、分子と分母のどちらも p を素因子として持たないということを、場合分けをして詳しく説明します。

(pⁿr – k)/k を既約分数としたときに、分子と分母のどちらの整数も p を素因子と持たないことが次のようにして示せます。

k を割り切る p の最高ベキが p⁰ のとき、すなわち、k が p を素因子として持たない場合は、分母の k は p を素因子として持っていません。

このとき、pⁿr – k ≡ k (mod p) で、k は p を素因子に持たないので、分子も p を素因子として持たないことになります。

k = p^st, s は自然数で、t は 自然数で p を素因子として持たないとします。

つまり、k は p で割り切れて、その最高ベキが p^s の場合です。

このとき、1 ≦ k ≦ pⁿ – 1 なので、k を割り切る p の最高ベキは p^n-1 以下となります。
そのため、s ≦ n – 1 です。

分子と分母が p^s で約分できるので、
(pⁿr – k)/k = (pⁿr – p^s)/p^st
= (p^n-sr – 1)/t

p^n-sr – 1 は p で割った余りが 1 なので、p で割り切れません。

t も p で割り切れないので、分子も分母も p を素因子として持っていないということになります。【証明完了】

ここから、組合せの考え方と群の作用の考え方を使います。

位数がpのn乗の部分集合全体

有限群 G を割り切る素数 p の最高ベキを pⁿ とします。

すなわち、| G | = pⁿr で、r は p で割り切れない自然数とします。

このとき、G の部分集合で位数が pⁿ となっているものをすべて集めたものを X とします。

X = {T₁, … , T_m}（ただし、各 | T_i | は pⁿ）

この m は、異なる pⁿr 個の G の元から pⁿ 個の元を選ぶ選び方の総数なので、
m = _pⁿrC_pⁿ です。

ここで、先ほど示した【補題1】より、
m と r を割り切る p の最高ベキは同じということになります。

この部分集合たちの集まり X に G を作用させることを考えます。

g ∈ G に対して、gT_i = { gx | x ∈ T_i } とすると、| gT_i | = | T_i | = pⁿ なので、位数が pⁿ の G の部分集合だから、gT_i ∈ X

したがって、
G × X → X, (g, T_i) → gT_i

は、G における結合律と単位元の定義から 作用となっています。

※ 共役類という記事で、作用の定義や軌道の個数やラグランジュの定理についての定理を解説しています。

軌道の個数についての一般論から次のことが分かります。

T_i を含む G-軌道を K とし、T_i の固定部分群を H とすると、| K | = |G/H|

この内容を使って、次の定理を証明します。シロー部分群の存在証明になります。

数学の証明では、より一般的にする方が証明をしやすいときもあります。

次の定理は、有限群 G の p-部分群の存在です。

G の位数が素数 p の最高ベキだけでなく、とにかく p ベキで割り切れると、その p ベキを位数とする部分群が存在するという定理になります。

シローの定理 :シローp-部分群の存在証明

【定理1】

p を素数とし、n を自然数とする。
群 G が | G | = pⁿr（ただし、r は自然数）とすると、位数 pⁿ の G の部分群が存在する。

＜証明＞

r を割り切る p の最高ベキを a ≧ 0 とします。すなわち、r は p^a で割り切れるが p^a+1 では割り切れないとします。

G の部分集合で位数が pⁿ となっているものをすべて集めたものを X とします。

X = {T₁, … , T_m} が、この部分集合系です。

【補題1】より、m = _pⁿrC_pⁿ を割り切る p のベキと r を割り切る p のベキは同じになります。

そのため、| X | = m は p^a で割り切れるが、
p^a+1 では割り切れないということになります。

群 G から X への作用についての軌道分解を
X = K₁ ∪ … ∪ K_b とします。

位数について、
| X | = | K₁ | + … + | K_b |
※ i ≠ j のとき K_i ∩ k_j = Φ

ここで、すべての G-軌道の位数が p^a+1 で割り切れるとすると、| X | が p^a+1 で割り切れることになってしまいます。

すると、| X | = m は p^a+1 では割り切れないことに反してしまいます。

そのため、少なくとも 1 つは p^a+1 で位数が割り切れない G-軌道が存在することになります。その軌道を K_c とします。

T_i ∈ K_c を一つ取り、T_i の固定部分群を H とすると、軌道に含まれている元の個数は、H の G における指数となります。

よって、| K_c | = |G/H|

ラグランジュの定理より、
|G/H| = | G | ÷ | H | なので、両辺に | H | を掛けると、| K_c | × | H | = | G | = pⁿr

r を割り切る p の最高ベキは p^a なので、右辺を割り切る p の最高ベキは p^n+a です。

左辺 | K_c | × | H | と右辺が等しいので、
| K_c | × | H | を割り切る p の最高ベキが p^n+a です。

| K_c | を割り切る p の最高ベキが p^a だったので、素因数分解の一意性から、| H | が pⁿ で割り切れることになります。

よって、| H | は pⁿ で割り切れるので、
pⁿ ≦ | H | … ★

一方、G から X への作用の定義と、H が T_i の固定部分群だったことから、a ∈ T_i とすると、
Ha ⊂ HT_i = T_i となります。

つまり、| H | = | Ha | ≦ | T_i| = pⁿ

★より、| H | = pⁿ

この固定部分群が求める位数 pⁿ の部分群です。【証明完了】

これで有限群 G の位数が素数 p の n 乗で割り切れたときに、必ず位数 pⁿ の G の部分群が存在するということが示せました。

用語について

位数が素数 p のベキとなっている群を p-群といいます。

また、群 G の位数を割り切る素数 p の最高ベキを n としたとき、位数 pⁿ の G の部分群のことを G のシローp-部分群といいます。

G のシローp部分群の位数が pⁿ のとき、
位数が p, p², … , p^n-1 の G の部分群を G の p-部分群といいます。

＜例＞

群 G の位数を、
| G | = 2023 = 7 × 17 × 17 とします。

このとき、位数 7 の部分群がシロー7-部分群です。

位数が 17² の部分群がシロー17-部分群です。
位数が 17 の部分群が 17-部分群です。

実は、このとき、17-部分群を 1 つ取ると、必ずその 17-部分群は、あるシロー17-部分群に含まれているということが示されます。

この内容の定理を証明するために、補題を証明します。

たた、補題を示すにあたって、定義を一つ述べておきます。

もう一つの補題

＜正規化群＞

群 G の部分集合を S とします。
このとき、{ g ∈ G | gSg-1 = S } は G の部分群となります。

この部分群を G における S の正規化群といい、N_G(S) と表記します。

【補題2】

P を群 G のシローp-部分群とし、H を位数が p ベキである| G の部分群とする。

このとき、
H ⊂ N_G(P) ならば、H ⊂ P である。

＜証明＞

H ⊂ N_G(P) より、HP が G の部分群となります。

実際、g, h ∈ H, a, b ∈ P とすると、

(ga)(hb)^-1 = (ga)(b^-1h^-1)
= (gb^-1)(b(ab^-1)h^-1) ∈ HP

ga, hb ∈ HP について、
(ga)(hb)^-1∈ HP となったので、HP は G の部分群です。

また、P は HP の正規部分群となっています。
g ∈ H, a, x ∈ P とすると、
(ga)x(ga)^-1 = g(axa^-1)g^-1

部分群の定義より、axa^-1∈ P であり、
仮定より、a ∈ H ⊂ N_G(P) なので、
g(axa^-1)g^-1∈ gPg^-1 = P だから、
(ga)x(ga)^-1∈ P

よって、P は HP の正規部分群です。

ここで、第二同型定理より、
HP/P と H/H∩P は群として同型となります。

※ 第二同型定理の証明はリンク先の記事で解説しています。

よって、位数について、
|HP| = | P | × |H/H∩P|
= | P | × | H | ÷ |H∩P|

仮定より、| P | と | H | は p ベキであり、H ∩P も P の部分群だから |H∩P| も p ベキです。

※ つまり HP が G の p-部分群ということです。

よって、|HP| も p ベキとなります。

※ P ⊂ HP なので、|HP| は 2 以上となっているので、p⁰ ではありません。

|HP| が p ベキで、P が HP の正規部分群ということになります。

P はシローp-部分群でした。

そのため、|HP| ≦ | P | となり、
HP = P となります。【証明完了】

この【補題2】を使って、次のシローの定理を証明します。

部分群の定義から、P ⊂ N_G(P) となっていることにも注意です。

シローの定理 :p-部分群はシローp-部分群の中

【定理2】

群 G の p-部分群 H は、
ある G のシローp-部分群 P に含まれる。

＜証明＞

G から G の空でない部分集合全体 X への共役作用を考えます。

g ∈G の S ⊂ G に対する作用は、gSg^-1 です。

この共役作用について、P の固定部分群は正規化群 N_G(P) です。

P を含む G-軌道を T = { P₁, … , P_s }
（ただし、P = P₁）とします。

| T | = s = |G/N_G(P)| であり、
P ⊂ N_G(P) なので、ラグランジュの定理から、N_G(P) は素因子として p をもちます。

その p ベキは、G の位数を割り切る最高ベキとなっています。

よって、|G/N_G(P)| は p を素因子として持たないので、等しい s も p を素因子として持ちません。

ここで、
T = {gPg^-1 | g ∈ G} ⊃ {hPh^-1 | h ∈ H}

よって、H から T への共役作用について、T の軌道分解を考えることができます。

このとき、各 H-軌道の位数は、H における固定部分群の指数となることから、| H | の約数となります。

実際、P_i ∈ T を含む H-軌道の位数は、
|H/N_H(P_i)| です。

H は p-部分群であり、N_H(P_i) は H の部分群なので、|H/N_H(P_i)| = p^r_i (r_i ≧ 0) という形です。

T を H-軌道に分解し、それらの軌道の位数をすべて足すと | T | = s となります。

軌道分解に現れるすべての H-軌道が p を素因子としてもつと、s は p を素因子として持たないことに反してしまいます。

よって、ある H-軌道 { hP_kh^-1 | h ∈ H } が存在して、|H/N_H(P_k)| = p⁰ = 1

これは、H = N_H(P_k) ということです。

特に H ⊂ N_H(P_k) なので、
【補題2】より、H ⊂ P_k

T の定義から、ある g₀ ∈ G が存在して、
g₀Pg₀^-1 = P_k であり、g₀Pg₀^-1 が P_k と同じ位数の G の部分群なので、P_k はシローp-部分群です。【証明完了】

この【定理2】から次の【定理3】が即座に導かれます。

シローp-部分群は互いに共役

【定理3】

群 G のシローp-部分群を P と P’ とすると、P と P’ は互いに共役である。

＜証明＞

T = {gPg^-1 | g ∈ G} とし、【定理2】の H として P’ を考えます。

【定理2】の証明より、
ある P_k ∈ T が存在し、P’ ⊂ P_k

P’ も P_k も G のシローp-部分群なので、同じ位数だから、P’ = P_k

T の定義から、P と P_k が共役なので、P と P’ は共役です。【証明完了】

今、証明した【定理3】の内容を踏まえた上で、もう一度、共役作用についての P を含む G-軌道を考えてみます。

T = {gPg^-1 | g ∈ G} は、シローp-部分群どおしが互いに共役であることから、G におけるすべてのシローp-部分群全体ということになります。

このことから、シローp-部分群の個数を表す次の定理を導きます。

シローの定理 :シローp-部分群の個数

【定理4】

群 G のシローp-部分群の個数を r とする。
このとき、r は | G | の約数で、
r = 1 + pk （ k は非負整数）という形である。

＜証明＞

P を G のシローp-部分群とし、
T = { gPg^-1 | g ∈ G } とします。

【定理3】より、シローp-部分群どおしは互いに共役だから、r = | T | = |G/N_G(P)|

|G/N_G(P)| は | G | の約数なので r は | G | の約数であることが示せました。

G におけるシローp-部分群の個数が 1 個しかないときは、k = 0 として定理が成立します。

そのため、以下において、G におけるシローp-部分群が 2 個以上の場合を考えます。

P = P₁ と異なる シローp-部分群を P₂ , … , P_r とします。

ただし、r は 2 以上の自然数です。そして、P から T への共役作用を考えます。

i を 2 以上 r 以下の任意の自然数とすると、
P = P₁ と P_i が互いに共役であることから、P_i を含む P-軌道には、P と P_i が含まれています。

そのため、P_i を含む P-軌道の位数は 1 より大きいことになります。

|P/N_P(P_i)| が、この軌道の位数なので、
|P/N_P(P_i)| > 2 となります。

よって、|P/N_P(P_i)| は | P | の約数なので p ベキですが、p⁰ ではありません。

そして、P から P = P₁ への共役作用では、P₁ は動かないことから、P₁ を含む P-軌道は、{P₁} となります。

よって、
P から T への共役作用についての軌道分解を、
T = S₁∪S₂∪ … ∪S_a
（ただし、a ≧ 2, S₁ = {P₁}）とすると、
2 ≦ x ≦ a について、|S_x| は p ベキで 2 以上の自然数です。

そのため、|S_x| は素数 p の倍数となっています。

一方、|K₁| = 1 なので、
r = | T | = |S₁| + |S₂| + … + |S_a|
= 1 + pk（ただし、k は自然数）

以上より、いずれの場合にせよ、
r = 1 + pk （ k は非負整数）という形になっています。【証明完了】

この【定理4】を使うときに、
k = 0 なのか、k ≧ 1 なのかということには注意が必要です。

実際に k が 0 となるときがあります。

具体例

実際に【定理4】における k が 0 になっている例です。

位数 6 の群 G について、シロー3-部分群の個数を考えてみます。

シロー3-部分群の個数を r とすると、r は 6 の正の約数で、r = 1 + 3k という形です。

k = 1 とすると、r = 4 で、6 の約数でないので不適です。k ≧ 2 とすると、r > 6 なので不適です。

したがって、k = 0 となり、r = 1 です。

シロー3-部分群の個数は 1 個なので、唯一のシロー3部分群は、正規部分群ということになります。

※ より詳しくは、シロー2-部分群とシロー3-部分群のそれぞれは巡回群で、a と b をそれぞれの生成元とすると、a と b で生成される群になっています。

※ 位数pqの群というブログ記事で内直積と半直積の観点から解説をしています。

これで、今回の記事を終了します。

読んで頂き、ありがとうございました。