二面体群 | 生成元についての関係式を正方形の合同変換で具体的に理解する

2023年3月29日

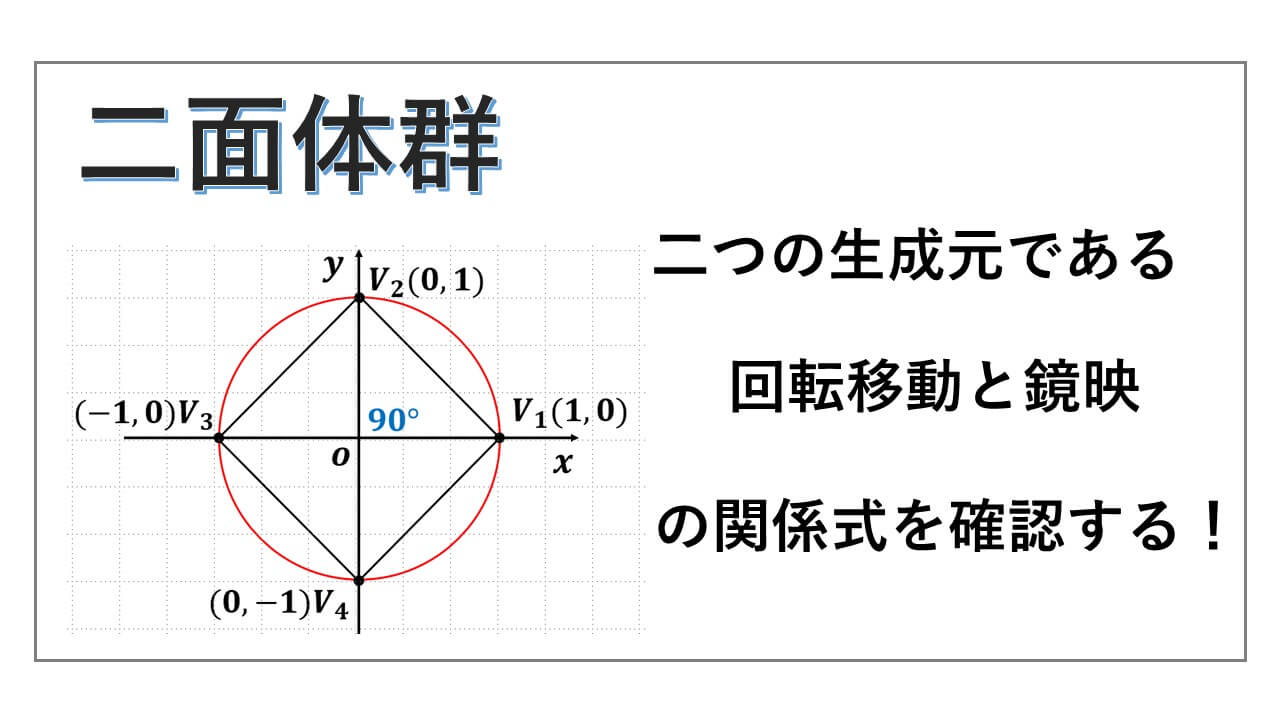
" 二面体群 “は、二つの生成元によって生成されている有限個の元から成る群です。

図形の形を変えない合同変換によって生成される群を正方形の対称性を視覚的に見ながら観察し、xy座標における点と点の線形変換を通じて、具体的に解説をしています。

合同変換というのは、図形の形を変えない変換です。

「平行移動、回転移動、直線に対する折り返し」という高校の数学で馴染みのある変換を用いた群を考えます。

図形的に群の作用（置換）による点の動きをイメージできるので、学習をし始めるときに良い例かと思います。

xy座標平面からxy座標平面への線形変換を考えます。

二つの線形変換で生成される正方形の二面体群について、生成元と関係式について解説をします。

二面体群 :生成される群

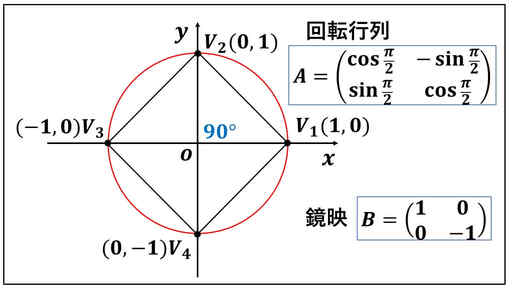
行列 A は、原点中心の左回り 90°の回転を表す行列です。

B は、y = 0、つまり、x 軸（横軸）について点を折り返すという鏡映を表します。

A が表す線形変換を f、B が表す線形変換を g とします。

f, g は xy-座標平面 R × R から xy-座標平面への線形変換となっています。

A と B の行列式が 0 でないので、どちらも逆行列をもちます。

そのため、f と g は逆写像 f^-1, g^-1 をもちます。

f と g は、図の正方形の四点を置換します。

f だと、頂点 V₁ を原点を中心として左回りに 90° 動かします。すると、V₁ は V₂ に移動します。同じく V₂ を中心角 90° で左回りに回転させると、V₃ に移ります。

f によって、V₃ は V₄ へ、V₄ は V₁ へと移動します。

このため、f という線形変換を施すと、
正方形V₁V₂V₃V₄ は、
正方形V₂V₃V₄V₁ へと移動します。

移動した後の図形の形は、同じ単位円周上に四つの頂点がある合同な正方形です。

線形変換を施した後も、施す前の図形と合同になっている合同変換です。g についての頂点の動きも押さえておきます。

x 軸についての折り返しなので、V₁ は V₁ へ移動します。

g について、点 V₁ は動かない固定点です。同じく軸上にある V₃ も動きません。

一方、V₂ は x 軸について対称に折り返されるので、V₄ へ移動します。V₄ は、その逆の動きで、折り返されて V₂ へ移動します。

そのため、
正方形V₁V₂V₃V₄
　　↓ g
正方形V₁V₄V₃V₂

鏡映 g を施した前後で、正方形は合同な同じ図形のままです。

これら、f, g という可逆な線形変換によって生成される群を考えます。

演算の定義

f と g で生成される群を考えるのですが、群の二項演算として、写像の合成を考えます。

xy-座標平面についての線形変換どおしの写像の合成が積なので、結合律が成立しています。

恒等写像 e も、正方形V₁V₂V₃V₄ の合同変換です。恒等写像なので、どの点も動かしません。

ちなみに、e を表す行列は、2 次の単位行列です。

また、f の逆写像 f^-1 は、原点を中心とする左回り 270° の回転を表す線形変換です。

逆写像より、f^-1f = e = ff^-1

原点を中心に点を左回りに 90° 回転させてから、さらに 原点中心に左回り 270° の回転を行うと、360° 回転したことになります。

これは、結局、点を動かさなかったことと同じということです。

同様に、270° 回転させてから 90° 回転させると、360° 回転で動かさなかったということになります。

x 軸についての折り返しである g だと、g 自身が g の逆写像となっています。

x 軸について折り返してから、もう一度折り返すと、もとの点に戻ります。

つまり、V₂ → V₄ → V₂

合成写像の記号を使って、表すと、
g²(V₂) = g(g(V₂)) = g(V₄) = V₂

同じく、g²(V₄) = V₂ です。

さらに、g²(V₁) = V₁, g²(V₃) = V₃ なので、g² はどの点も動かしていません。

g を表す行列 B ですが、B と B で行列の乗法を計算すると単位行列になっています。

f を 表す行列 A についても、4 乗したときに初めて単位行列となります。

表現行列が具体的に分かっているので、行列を計算することで、f の位数は 4 で、g の位数が 2 ということが、すぐに分かります。

以上の内容から、写像の合成を積とする f と g で生成される群 G を定義することができます。

生成と最小性

可逆な線形変換 f と g で生成される群 G というものを特徴づけます。

f と g を含む包含関係についての最小の群というのが、生成される群の定義です。

この定義のままだと、よく分からないので、f と g で生成される群というものを特徴づけます。

【命題】

f と g を含む包含関係についての最小の群を G とする。

この G は、f, g, f^-1, g^-1 の 4 個の線形変換を有限個で積をとったもの全体である。

＜証明＞

f, g, f^-1, g^-1 の 4 個の線形変換を有限個で積をとってできた線形写像は、群 G に含まれています。

そのため、f, g, f^-1, g^-1 の 4 個の線形変換を有限個で積をとったもの全体 H が、G の部分群となっていることを示せば、最小性から H と G が一致します。

x_i (i = 1, 2, 3) をそれぞれ f, g, f^-1, g^-1 のどれかだとすると、
x₁(x₂x₃) = (x₁x₂)x₃ です。

で、x₁x₂x₃ は可逆な線形変換で、正方形の形を変えない合同変換になっています。

そして、f, g, f^-1, g^-1 の 4 個の線形変換を有限個で写像の合成をしたものどおしを合成しても、やはり、f, g, f^-1, g^-1 の 4 個の線形変換を有限個で写像の合成したものです。

これで、H が積で閉じていて、結合律が成立していることが確認できました。

x_i (i = 1, … , n) を f, g, f^-1, g^-1 のどれかだとすると、x₁x₂…x_n の逆写像は、
x_n^-1…x₂^-1x₁^-1 です。

つまり、
(x₁x₂…x_n)^-1 = x_n^-1…x₂^-1x₁^-1

これで、逆元で閉じていることも分かりました。

したがって、H ⊂ G であり、H は f, g, f^-1, g^-1 を含む群なので、G の最小性から H と G は一致します。【証明完了】

これで、命題が証明できたので、だいぶ f, g, f^-1, g^-1 を含む群 G が具体的になってきました。

ここからは、G の二つの生成元についての関係式について考察します。

二面体群 :生成元と関係式

f と g の二元で生成される群 G を

G = ＜f, g＞ と表すことにします。

先ほど証明した命題から、G は f, g, f^-1, g^-1 の 4 個の線形変換を有限個で積をとったものです。

有限個の元で生成されている有限群があったら、各生成元の位数と、異なる生成元で積をとったときの関係式が知りたいところです。

位数については、f が 4 で、g が 2 ということが分かっています。後は、f と g についての関係式です。

f は原点を中心とする左回り 90° の回転移動です。g は x 軸についての折り返しでした。そこで、合成変換 fg について、各正方形の頂点の動きを調べてみます。

g は x 軸上の点を動かさないということに注意して、それぞれの点の移動先を調べます。

fg(V₁) = f(V₁) = V₂ です。残りの 3 つの点の移動先も見てみます。

g は V₂ と V₄ の入れ替えでしたので、　

fg(V₂) = f(V₄) = V1,
fg(V₃) = f(V₃) = V₄,
fg(V₄) = f(V₂) = V₃,

よって、
正方形V₁V₂V₃V₄
　　↓ fg
正方形V₂V₁V₄V₃

さらに g で移してみます。

正方形V₂V₁V₄V₃
　　↓ g
正方形V₄V₁V₂V₃

今、gfg という三個の線形変換の合成を施しました。正方形の動きについて、動かす前と、三個で動かした後を見比べてみます。

正方形V₁V₂V₃V₄
　　↓ gfg
正方形V₄V₁V₂V₃

これは、正方形V₁V₂V₃V₄ を原点中心に左回りに 270° 回転させたことになります。

実際、行列の計算をすると、f を 表す行列 A と、g を表す行列について、

BAB = A³ = A^-1 となっています。

g = g^-1 なので、g から f への共役作用の結果が分かりました。

gfg^-1 = f^-1 となっています。
(もしくは、gfg^-1 = f³)

gfg^-1 ≠ f なので、f と g は可換ではないということも分かりました。
　
G における一元生成の巡回部分群も用意しておきます。

{e, g} = ＜g＞,
{e, f, f², f³} = ＜f＞

よって、二面体群 G は、

＜f, g | f⁴=g²=e, gfg=f^-1＞ となっています。

この関係式を手掛かりに、G の位数を調べます。

G=<f><g>の証明

e = f⁰ = f⁴, e = g² として、

{fⁱg^k | 0≦i≦3, 0≦k≦2}
= ＜f＞＜g＞ を考えます。

gfg = f^-1 で、g^-1 = g なので、

gf = f^-1g = f³g となっています。

＜f＞＜g＞ が G の部分群となっていることを示します。

(fⁱ)^-1 = f^4-i, (g^k)^-1 = g^2-k なので、

＜f＞＜g＞ の任意の元を
f^i₁g^k₁, f^i₂g^k₂ とすると、

(f^i₁g^k₁)(f^i₂g^k₂)^-1 = (f^i₁g^k₁)(g^2-k₂f^4-i₂)
= f^i₁g^2+k₁-k₂f^4-i₂

ここで、g の位数は 2 なので、
g^2+k₁-k₂ = e または g です。

g^2+k₁-k₂ = e の場合、

(f^i₁g^k₁)(f^i₂g^k₂)^-1 = f^i₁f^4-i₂
= (f^i₁f^4-i₂)g⁰ ∈ ＜f＞＜g＞

g^2+k₁-k₂ = g の場合、

(f^i₁g^k₁)(f^i₂g^k₂)^-1 = f^i₁gf^4-i₂

ここで、f^4-i₂ = e だと、
f^i₁gf^4-i₂ ∈ ＜f＞＜g＞ です。

f^4-i₂ が f, f², f³ のどれかだとすると、
gf = f^-1g なので、
f^i₁gf^4-i₂ ∈ ＜f＞＜g＞ です。

よって、いずれの場合であっても、

(f^i₁g^k₁)(f^i₂g^k₂)^-1∈ ＜f＞＜g＞

ゆえに、部分群の判定方法より、

＜f＞＜g＞ は G の部分群です。

f^-1 = f^-1e, g^-1 = eg^-1 なので、
＜f＞＜g＞は、f, g, f^-1, g^-1 という 4 個の元を全て含んでいます。

G は f, g, f^-1, g^-1 という 4 個の元を全て含んでいる最小の群だったので、

G = ＜f＞＜g＞ となります。

次に 有限群 G の位数を決定します。

二面体群 :Gの位数は8

G = ＜f＞＜g＞ の位数を決定します。

＜f＞＜g＞ = ＜f＞∪＜f＞g

f は、頂点 V₁, V₂, V₃, V₄ のどのも固定しないので、g は ＜f＞ に含まれていません。

また、g は V₂ を V₄ に移すので、恒等変換 e とは異なります。

よって、右剰余類＜f＞と＜f＞g の共通部分は空集合です。回転角の違いから、＜f＞ は、4 個の元が含まれています。

0 ≦ i₁ < i₂ ≦ 3 について、
f^i₁g = f^i₂g だと仮定すると、
f^i₁ = f^i₂ となり、i₁ < i₂ に反してしまうので、
f^i₁g ≠ f^i₂g です。

よって、＜f＞g には 4 個の元が含まれています。

以上より、
＜f＞∪＜f＞g = G に含まれている元の個数は、4 + 4 = 8 となります。

これで、正方形V₁V₂V₃V₄ の形を変えない二つの合同変換で生成された二面体群の元の位数が 8 だと分かりました。

直積分解ではない

G = ＜f＞＜g＞ で、＜f＞と＜g＞の共通部分は単位元 e のみです。しかし、これは内直積ではありません。

理由は、＜f＞と＜g＞が可換でないからです。

部分群 K₁ と K₂ の内直積に分解していたとすると、K₁ の任意の元と K₂ の任意の元が可換となっています。

しかし、はじめの方で確認したように、
gfg^-1 ≠ f なので、f と g は可換ではありませんでした。

そのため、G = ＜f＞＜g＞ は内直積ではありません。

最後に合同変換群の例について述べておきます。

合同変換群 :図形の頂点の置換

正十二面体を正十二面体に移す合同変換を考えます。

正十二面体を合同変換で動かすと、十二個の頂点が、置換されることになります。

そのため、正十二面体の頂点の動きに焦点を当てると、異なる 20 個の頂点の置換（入れ替え）と考えることができます。

そこで、正十二面体の合同変換を 20 個の頂点全体 Ω に制限することにより、Ω上の置換群の部分集合と考えることができます。

ただし、十二個の面をバラバラにして入れ替えてから、つなぎ合わせるということは合同変換とは考えません。

あくまで正十二面体の回転移動のような形を変えない変換について考えています。

そのため、Ω上の置換は 20! 個ありますが、合同変換であるために、頂点の置換には制約がつきます。

また、正十二面体を全く動かさないという恒等変換も合同変換の一つと定義します。

さらに、正十二面体の合同変換を二つの合成写像も正十二面体の合同変換です。

そして、合同変換の逆置換も正十二面体の合同変換です。

これで、恒等変換を単位元とし、Ωの置換群が得られました。

正十二面体の合同変換群を、Ωという 20 個の頂点から成る集合の置換群とみなして議論を進めます。

正二十面体についても、同様に 12 個の頂点の置換群として考えます。

誘導される合同変換

ここで、正十二面体群に含まれる元の個数を求めることを考えます。

そのために、正二十面体群との関係を考えます。

正十二面体を合同変換で動かすと、内接している正二十面体も動かすことになります。

すると、正十二面体の合同変換は、内接する正二十面体の 12 個の頂点を置換することになります。

そのため、正十二面体の 20 個の頂点全体Ω を表す置換は、内接する正二十面体の 12 個の頂点全体から成る集合の置換となります。

そのため、正十二面体の合同変換を20次対称群の置換と考えていたわけですが、その置換から、12 個の頂点の置換が得られることになります。

そのため、正十二面体の合同変換群は、正二十面体の合同変換群に埋め込まれます。

逆に、正二十面体の合同変換群は、内接する正十二面体の合同変換群に埋め込まれます。

どちらも 20次や 12次の対称群の部分群だったので、有限群です。

正十二面体の合同変換群と正二十面体の合同変換群は、群同型になっています。

同型なので、正十二面体群の位数と正二十面体群の位数が同じになっています。

群同型写像で保存される性質については、扱いやすい方で議論して調べることができます。

正十二面体群の位数を求めるために、正二十面体群の位数を求めます。

十二個の頂点の置換

正二十面体の合同変換で、十二個の頂点が置換されます。

まず、この正二十面体群の置換が、十二個の頂点の頂点から、どの二つの頂点を取ってきても、置換で移り合うことを示します。

a₁, … , a₁₂ を正二十面体の頂点とし、これら 12 個の頂点全体から成る集合を X とします。

a_i は恒等置換で a_i に移ると考えるため、異なる頂点が、移り合うことを示します。

正二十面体群を H とし、
{h(a₁) | h∈H} という軌道を考えます。

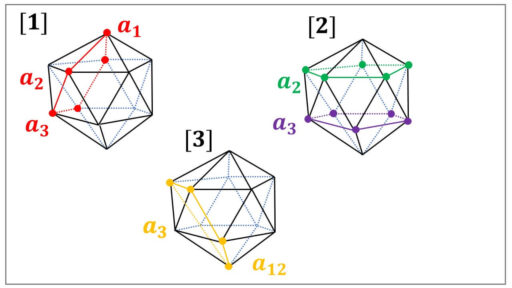
[1] で、赤色の正五角形を重心を中心に 72°回転させるという合同変換を f∈H とします。

f と f の合成を f²∈H です。

a₂ = f(a₁)∈{h(a₁) | h∈H},
a₃ = f²(a₁)∈{h(a₁) | h∈H} です。

[2] で、緑色の正五角形の中心角 72°の回転を s, 紫色の正五角形の中心角 72°の回転を t とします。

sⁱ, t^j (1, j = 1, … , 5) は H の元です。

sⁱf, t^jf という合成も H の元です。

そのため、
sⁱ(a₂) = (sⁱf)(a₁),
t^j(a₃) = (t^jf)(a₁) は、
{h(a₁) | h∈H} に含まれています。

つまり、{h(a₁) | h∈H} に緑色や紫色の頂点が、全て含まれることになります。

最後に、[3] で、オレンジ色の正五角形の中心角 72°の回転を k とします。

kf²∈H です。

そのため、
a₁₂ = k(a₃) = (kf²)(a₁) は、
{h(a₁) | h∈H} に含まれています。

これで、{h(a₁) | h∈H} に十二個の頂点が全て含まれることが分かりました。

逆置換も合わせると、
{h(a₁) | h∈H} に含まれている任意の二点は、合同変換による置換で移り合うということになります。

{h(a₁) | h∈H} = X というように、群の置換作用を受ける集合の任意の二点が移り合うとき、群の置換作用が推移的であるといいます。

ここで、作用について、軌道に含まれている元の個数についての性質を使います。

この G(a) という固定部分群は、a を動かさない G の元たちです。

先ほどの図を用いた内容では、置換作用をする群が H で、有限集合 X の元 a₁ を含む軌道を考えました。

H の置換作用は推移的で、a₁ を含む軌道は X に一致していました。

そのため、
|O(a₁)| = |X| = 12 です。

次に、
H(a₁) = {h∈H | h(a₁) = a₁} という固定部分群の位数が分かれば、H の位数が計算で求まることになります。

h∈H(a₁) とすると、h は十二個の頂点の置換であり、かつ頂点 a₁ を動かさない置換です。

そうすると、頂点 a₁ と辺で結ばれている五個の頂点の h による像の位置が絞られます。

頂点 a₁ と辺で結ばれている正五角形の頂点を x₁, x₂, x₃, x₄, x₅ とします。

正十二面体の形を変えない合同変換ですから、
1 ≦ i ≦ 5 について、
h(x_i) は h(a₁) = a₁ と辺で結ばれていることになります。

そのため、h は、正五角形の置換と考えられます。

正五角形x₁x₂x₃x₄x₅ の隣接関係を変えることはできません。

そのため、h は、これら五個の頂点の巡回置換 σ または、そのベキ乗となります。

つまり、
σ = (x₁, x₂, x₃, x₄, x₅),
または σ^r (r は整数) です。

σ^-1 = σ4 なので、h は、
σ⁰, σ¹, σ², σ³, σ⁴ の 5 個のいずれかになります（σ⁰ は恒等置換）。

これで、H(a₁) の位数が 5 と分かりました。

よって、
|H| = |O(a₁)| × |H(a₁)|
= 12 × 5 = 60

以上より、正二十面体群の位数が 60 で、正十二面体群の位数と等しいため、正十二面体群の位数も同じ 60 です。

それでは、これで今回のブログ記事を終了します。

読んで頂き、ありがとうございました。