ツァッセンハウスの補題 Zassenhaus | 証明は、対称な形であることを利用する

" ツァッセンハウスの補題 (Zassenhaus’s lemma)"の証明について解説をしています。
仮定と結論に対称な形が見えることから、片方について証明できることを、文字を入れ替えて、もう片方についても同様の議論をすることができます。
すべてを記述すると大変ですが、対称な形を利用して、機械的に入れ替えで済む部分を円滑に進めます。
この補題は、シュライアーの細分定理もしくはジョルダン・ヘルダーの定理を証明するときに効果を発揮します。
剰余群について、第二同型定理や第三同型定理を用い、同型対応を考えるので、基本を丁寧に踏まえることが理解につながるかと思います。
まず、片方について成立する内容を命題の形で、いくつか述べます。形が対称なことを利用すると、自動的に、もう片方について成立する命題が得られます。
この記事では、e を群 G の単位元として表しています。
ツァッセンハウスの補題 :準備の命題
【命題1】
G を群とし、H と K を G の部分群とする。また、S を H の正規部分群とする。
このとき、S は S(H∩K) の正規部分群で、
S(H∩K) ≅ H∩K/K∩S である。
<証明>
S が H の正規部分群で、H∩K も H の部分群なので、S(H∩K) は H の部分群となります。
実際、x, y∈S(H∩K) とすると、
s1, s2∈S, a, b∈H∩K が存在して、
x = s1a, y = s2b と表せます。
xy-1 = (s1a)(b-1s2-1)
∈ (Sa)(b-1S) = S((ab-1)S) = S(S(ab-1))
= (SS)(ab-1) = S(ab-1) ⊂ S(H∩K)
(剰余類について、(ab-1)S = S(ab-1) となるのは S が正規部分群だからです。)
部分群の判定方法から、S(H∩K) は部分群ということが分かりました。
また、S は H の正規部分群なので、
S ⊂ S(H∩K) ⊂ H だから、
S は S(H∩K) の正規部分群となっています。
さらに、
(H∩K)∩S ⊂ H∩K ⊂ H より、
(H∩K)∩S は H∩K の正規部分群となっています。
実際、u∈(H∩K)∩S, w∈H∩K について、
u, w∈H∩K だから、wuw-1∈H∩K です。
そして、S が H の正規部分群だから、
u∈S, w∈H より、wuw-1∈S です。
そのため、wuw-1∈(H∩K)∩S なので、
(H∩K)∩S は H∩K の正規部分群です。
ここで、S が H の正規部分群だから、
S(H∩K) = (H∩K)S であり、
(H∩K)∩S = (K∩H)∩S = K∩(H∩S) = K∩S であることに注意して、第二同型定理を使います。
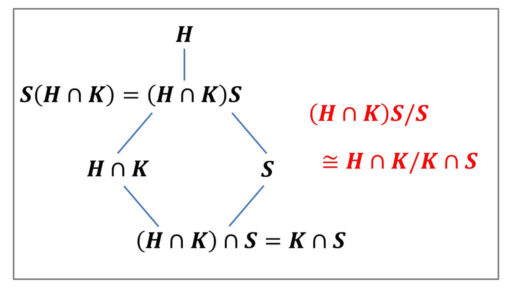
第二同型定理から、
(H∩K)S/S ≅ H∩K/K∩S ■
H と K, S と T を入れ替え、同様の議論をすることで、次の命題が成立します。
対称な形を利用する
【命題1’】
G を群とし、K と H を G の部分群とする。また、T を K の正規部分群とする。
このとき、T は T(K∩H) の正規部分群で、
T(K∩H) ≅ K∩H/H∩T である。
H と K、S と T を入れ替えて、同様の証明をします。
すると、この【命題1’】のときは、第二同型定理を使うと、
T(K∩H)/T ≅ K∩H/H∩T となります。
ツァッセンハウスの補題の仮定で、H と K、S と T が対称な形で設定されているので、【命題1】を導いたときと同様の議論で、【命題1’】が導けます。
二つずつ命題たちを対に証明していき、最終的にどちらも同じ形の群になることを示します。すると、ツァッセンハウスの補題の結論に至ります。
では次の命題です。再び H と S を主役にした形で証明すると、役割を入れ替えた K と T についての命題も成立することになります。
ツァッセンハウスの補題 :剰余群を定義するために
【命題2】
H と K を G の部分群とし、S を H の、T を K の正規部分群とする。
このとき、H∩T は H∩K の正規部分群である。
そして、(H∩T)(K∩S) は H∩K の正規部分群である。
<証明>
H∩T ⊂ H, H∩T ⊂ T ⊂ K より、
H∩T ⊂ H∩K です。
H∩T は G の部分群なので、H∩K の部分群となっています。
次に H∩T が H∩K の正規部分群であることを示します。
x∈H∩T, h∈H∩K とします。
T は K の正規部分群だから、
hxh-1∈T です。
x, h∈H なので、hxh-1∈H ともなっています。
よって、hxh-1∈H∩T なので、
H∩T は H∩K の正規部分群です。
【命題1’】の証明から、
K∩S = (H∩K)∩S でした。
(H∩K)∩S = H∩(K∩S) より、
K∩S = H∩(K∩S) ⊂ H です。
また、H∩T ⊂ H であり、
積で閉じているため、
(H∩T)(K∩S) ⊂ H … (1)
そして、
H∩T ⊂ T ⊂ K, K∩S ⊂ K なので、
(H∩T)(K∩S) ⊂ K … (2)
(1), (2) より、
(H∩T)(K∩S) ⊂ H∩K となっています。
先ほど示したことから、
H∩T は H∩K の正規部分群であり、
K∩S は H∩K の部分群なので、
(H∩T)(K∩S) は H∩K の部分群となっています。
さらに、(H∩T)(K∩S) が H∩K の正規部分群であることを示します。
xy∈(H∩T)(K∩S)(ただし、x∈H∩T, y∈K∩S)とします。
また、h∈H∩K とします。
h(xy)h-1 = (hxh-1)(hyh-1) … (3)
x, h∈H より、
hxh-1∈H です。
また、x∈T, h∈K より、
T は K の正規部分群だから、
hxh-1∈T です。
ゆえに、hxh-1∈H∩T … (4)
さらに、y∈K∩S ⊂ S ⊂ H,
h∈H より、
hyh-1∈H です。
そして、y∈K, h∈K より、
hyh-1∈K です。
ゆえに、hyh-1∈H∩K … (5)
(3), (4), (5) より、
h(xy)h-1∈(H∩T)(K∩S) です。
これで、(H∩T)(K∩S) が H∩K の正規部分群であることを示せました。 ■
H と K, S と T を入れ替えて、次の命題が同様にして導かれます。
同様に対称性から対になる命題
【命題2’】
K と H を G の部分群とし、T を K の、S を H の正規部分群とする。
このとき、K∩S は K∩H の正規部分群である。
そして、(K∩S)(H∩T) は K∩H の正規部分群である。
【命題2】の H と K 、S と T を入れ替え、【命題1’】を利用すると、同様にして証明ができます。
機械的な文字の入れ替え操作で、【命題2’】が得られました。
剰余群を定義するためにも、正規部分群となっていることを押さえました。
次の命題で、ツァッセンハウスの補題の片側が得られます。第二同型定理と第三同型定理のアンサンブルです。
ツァッセンハウスの補題 :片側の内容が登場
【命題3の前半】
H と K を G の部分群とし、S を H の、T を K の正規部分群とする。
このとき、S(H∩T) は S(H∩K) の正規部分群である。
<証明>
【命題1】より、
H∩K/K∩S ≅ S(H∩K)/S です。
この同型を与える群同型写像を f とすると、第二同型定理の証明から、f の対応は次のようになっています。
x(K∩S)∈H∩K/K∩S に対して、
f(x(K∩S)) = xS ∈ S(H∩K)/S
ここで、S は H の正規部分群なので、
x∈H となっているので、
剰余類について、xS = Sx です。
よって、(H∩T)(K∩S)/K∩S という剰余群の部分群の f による像は、
f((H∩T)(K∩S)/K∩S) = S((H∩T)(K∩S))/S
ここで、s∈S について、sS = S だから、
K∩S ⊂ S より、
S((H∩T)(K∩S))/S = S(H∩T)/S となります。
このことを各元について正確に見てみます。
s∈S, x∈H∩T, y∈K∩S とすると、
y∈S より、
(sxy)S = (sx)S ∈S(H∩T)/S
そのため、
S((H∩T)(K∩S))/S ⊂ S(H∩T)/S
逆に、s∈S, a∈H∩T とすると、
G の単位元 e について、
e が K∩S の単位元だから、
(sa)S = (sae)S ∈ S((H∩T)(K∩S))/S
そのため、
S(H∩T)/S ⊂ S((H∩T)(K∩S))/S
よって、
S((H∩T)(K∩S))/S = S(H∩T)/S となっています。
このことから、
f((H∩T)(K∩S)/K∩S) = S((H∩T)(K∩S))/S
= S(H∩T)/S です。
f は群同型写像なので、
(H∩T)(K∩S)/K∩S ≅ S(H∩T)/S と対応しています。
また、【命題2】より、
(H∩T)(K∩S) は H∩K の正規部分群だったから、
(H∩T)(K∩S)/K∩S は H∩K/K∩S の正規部分群です。
よって、群として同型だから、
S(H∩T)/S は S(H∩K)/S の正規部分群となっています。
同型対応を利用して、片方で正規部分群となっていると、同型対応をしている行き先でも、そうなっているということです。
ただし、正規部分群であることを示したいのは、S で剰余をとっていない状態です。もう少し考察を進めます。
任意に s1x∈S(H∩T), s2a∈S(H∩K) を取ります。
(ただし、s1, s2∈S, x∈H∩T, a∈H∩K です。)
S(H∩T)/S は S(H∩K)/S の正規部分群だから、
((s2a)(s1x)(s2a)-1)S
((s2a)S)((s1x)S)((s2a)S)-1
∈S(H∩T)/S
よって、ある s3∈S, y∈H∩T が存在して、
((s2a)(s1x)(s2a)-1)S = (s3y)S
ここで、s3, y∈H で、S は H の正規部分群だから、
(s3y)S = S(s3y) です。
さらに、S(s3y) = (Ss3)y = Sy
そのため、
((s2a)(s1x)(s2a)-1)S = Sy
y∈H∩T だから、
(s2a)(s1x)(s2a)-1∈S(H∩T)
よって、
S(H∩T) は S(H∩K) の正規部分群です。 ■
今、示した前半から、さらに群としての同型対応を導きます。
命題3の完成形
【命題3】
H と K を G の部分群とし、S を H の、T を K の正規部分群とする。
このとき、S(H∩T) は S(H∩K) の正規部分群である。
そして、
S(H∩K)/S(H∩T) ≅ H∩K/(H∩T)(K∩S) である。
<証明>
先ほど示した前半の内容から、
S(H∩T) は S(H∩K) の正規部分群なので、
剰余群 S(H∩K)/S(H∩T) を考えることができます。
【命題2】より、
(H∩T)(K∩S) は H∩K の正規部分群だったので、
(H∩T)(K∩S)/H∩S は H∩K/H∩S の正規部分群です。
第三同型定理より、
(H∩K/K∩S)/((H∩T)(K∩S)/K∩S)
≅ H∩K/(H∩T)(K∩S) … (4)
一方、【命題1】より、
H∩K/K∩S ≅ S(H∩K)/S であり、
前半の証明の内容から、
(H∩T)(K∩S)/K∩S ≅ S(H∩T)/S でした。
ゆえに、
(H∩K/K∩S)/((H∩T)(K∩S)/K∩S)
≅ (S(H∩K)/S)/(S(H∩T)/S)
ここで、第三同型定理より、
(S(H∩K)/S)/(S(H∩T)/S)
≅ S(H∩K)/S(H∩T)
よって、
(H∩K/K∩S)/((H∩T)(K∩S)/K∩S)
≅ S(H∩K)/S(H∩T) … (5)
(4), (5) より、
S(H∩K)/S(H∩T)
≅ H∩K/(H∩T)(K∩S) ■
この【命題3】も、H と K、S と T を入れ替えて同様の議論をすることで、次の命題を導けます。
やはり入れ替えて同様に
【命題3’】
K と H を G の部分群とし、T を K の、S を H の正規部分群とする。
このとき、T(K∩S) は T(K∩H) の正規部分群である。
そして、
T(K∩H)/T(K∩S) ≅ K∩H/(K∩S)(H∩T) である。
【命題3】について H と K の入れ替え、S と T の入れ替えをすると、得られる命題です。
【命題3】と【命題3’】には、ツァッセンハウスの補題の結論の同型となる群が現れています。
最後に、
H∩K/(H∩T)(K∩S) と
K∩H/(K∩S)(H∩T) が群として同型であることを示すと、ツァッセンハウスの補題の証明が完成します。
ツァッセンハウスの補題 :証明の完成
【ツァッセンハウスの補題】
H と K を G の部分群とし、S を H の、T を K の正規部分群とする。
このとき、S(H∩T) は S(H∩K) の正規部分群、
T(K∩S) は T(K∩H) の正規部分群である。
そして、
S(H∩K)/S(H∩T) ≅ T(K∩H)/T(K∩S) である。
<証明>
【命題3】より、
S(H∩K)/S(H∩T) ≅ H∩K/(H∩T)(K∩S)
【命題3’】より、
T(K∩H)/T(K∩S) ≅ K∩H/(K∩S)(H∩T)
H∩K = K∩H で、
H∩T は H∩S の正規部分群だから、
(H∩T)(K∩S) = (K∩S)(H∩T) です。
よって、
H∩K/(H∩T)(K∩S)
= K∩H/(K∩S)(H∩T)
すなわち、
S(H∩K)/S(H∩T) ≅ T(K∩H)/T(K∩S) ■
これで、ツァッセンハウスの補題の証明が完成しました。
【命題3】を証明したときに使った内容を補足しておきます。同型対応が絡むときに、使うときがある内容です。
証明で使った内容の補足
【命題3】の証明で、
H∩K/K∩S ≅ S(H∩K)/S と
(H∩T)(K∩S)/K∩S ≅ S(H∩T)/S から、
(H∩K/K∩S)/((H∩T)(K∩S)/K∩S)
≅ (S(H∩K)/S)/(S(H∩T)/S) を導きました。
この内容を一般的な内容で証明しておきます。
【命題】
f : G → G’ を群としての同型写像とする。そして、N, N’ をそれぞれ、G, G’ の正規部分群とする。
また、f(N) = N’ とする。(つまり、f に関して、N と N’ が同型対応。)
このとき、G/N ≅ G’/N’ である。
<証明>
f を用いて、Ψ という G/N から G’/N’ への写像を次のように誘導します。
gN∈G/N に対して、
Ψ(gN) = f(g)N’∈G’/N’ と定義します。
まず、代表元の取り方に依存しないで Ψ が定義できていることを示します。
gN = hN (g, h∈G) だとします。
すると、ある t∈N が存在して、
g = ht と表せます。
よって、
Ψ(gN) = f(g)N’ = f(ht)N’
=(f(h)f(t))N’ = (f(h)N’)(f(t)N’)
ここで、f(N) = N’ の仮定から、
t∈N より、f(t)∈N’ です。
そのため、G’ の単位元を e’ とすると、
f(t)N’ = eN’ なので、
Ψ(gN) = (f(h)N’)(f(t)N’)
= (f(h)N’)(e’N’)
= f(h)N’ = Ψ(hN)
これで、Ψ が代表元の取り方に依存せずに定義できていることが確認できました。
次に、Ψ が群としての準同型写像となっていることを示します。
g, h∈G に対して、
Ψ((gh)N) = f(gh)N’ = (f(g)f(h))N’
= (f(g)N’)(f(h)N’) = Ψ(gN)Ψ(hN)
これで、Ψ が準同型写像であることが示せました。
Ψ の単射性は、f が同型写像なので単射であることから従います。
Ψ(gN) = Ψ(hN)(g, h∈G) だとします。
すると、f(g)N’ = f(h)N’ です。
両辺に (f(h)N’)-1 = f(h-1)N’ を掛けると、
(f(g)N’)(f(h-1)N’) = N’ です。
よって、
N’ = (f(g)f(h-1))N’ = f(gh-1)N’
ここで、f の逆写像 f-1 も群同型写像だから、
N = f-1(N’) = f-1(f(gh-1)N’)
= f-1(f(gh-1))f-1(N’)
= (gh-1)N
このため、gh-1∈N となり、
gN = hN となります。
これで、Ψ が単射であることが示せました。
最後に、Ψ が全射であることを示します。
g’N’∈G’/N’ を任意に取ります。この g’ は G’ の元です。
f が全射なので、ある元 g∈G が存在して、
f(g) = g’ です。
そのため、gN∈G/N を Ψ で移すと、
Ψ(gN) = f(g)N’ = g’N’
これで、Ψ が全射であることも示せたので、Ψ は群同型写像であることが示せました。 ■
今回の記事の証明で用いた第三同型定理の証明や正規部分群の定義といった内容は、第二同型定理という記事で述べています。
証明したツァッセンハウスの補題を使うことで、ジョルダン・ヘルダーの細分定理を証明することができます。
これについては、組成列という記事で解説をしています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。