組成式 – 式量 | 分子式との違いについて解説

2023年8月14日

" 組成式 – 式量 “について高校の化学で学習する内容について解説しています。

分子式との違いを説明しています。

この記事では、単元を学習し始めたときに出てくるような基礎的な計算問題を、計算しやすいように数字を設定しています。

高校の化学を勉強するときに、リアルな内容にするために細かい数字が使われているかと思いますが、学習のしやすさを狙って、単純な数字に意図的にしています。

組成式と分子式の違いをしっかりと押さえることを目指し、違いが意識しやすくなるような簡単な練習問題を用意しています。

組成式 -式量 :分子式との違い

組成式は、学習をし始めるときに、「原子数の比を最も簡単な整数比で表したもの」というように述べられるかと思います。

例えば、C₆H₁₂O₆というグルコースという分子式を見てください。

原子の数について、
C : H : O が、
6 : 12 : 6 となっています。

この整数比は 6 で割ることで、簡単にできます。

6 : 12 : 6
= 1 : 2 : 1 となります。

この CH₂O が組成式です。

ちなみに、
C₆H₁₂O₆ = 180 が分子量です。

組成式についての
CH₂O = 30 を式量といいます。

(CH₂O) の 6 倍が、
C₆H₁₂O₆ となっています。

(CH₂O) を最小の固まりとして、これらが繰り返されてグルコースの分子式ができているという感じです。

原子量-分子量について学習をしてきて、組成列という新しい用語と定義が出てきました。

ただ、ここで、何で組成式というものを考えるのかという疑問が起きます。

それについて、これから組成式と分子式の違いを説明をします。

何で組成式を考えるのか

組成式という分子式とは違うものを用意するには、動機があるわけです。

いろいろと想定して定義が作られたわけですが、受け入れやすそうな状況を１つ述べておきます。

CO₂だと二酸化炭素の分子式です。

二酸化炭素だと、C 原子 1 個と O 原子 2 個の 3 個という少ない原子で二酸化炭素という物質の構成を表すことができています。

ところが、塩化ナトリウムの結晶のように、使われている全ての原子を表記すると数が多すぎる物質も存在します。

無理に表現しようとすると、
Na_10億Cl_10億というになってしまいます。

10億よりも多いかもしれません。

とにかく原子の数が多過ぎるという状況です。

そこで、
NaCl を繰り返しの最小の固まりとして考えるということをしました。

この NaCl という繰り返される固まりが組成式です。

組成式というものをわざわざ考える動機の１つとして、原子の数が多過ぎるので、最小の繰り返しを考えるということを挙げました。

文系の方で化学基礎だけを学習しているという方は、これくらいの内容で組成式と分子式の違いを気軽に押さえておけば良いかと思います。

一方、理系の方だと、有機化学の分野で組成式の計算問題が出てきます。

そのため、理系の方は組成式と分子式の違いを嫌でも認識することになります。

分子式は物質を構成している原子の数が確定しています。

それに対して、組成式だと、繰り返しの固まりが分かっているけれでも、物質を構成している原子の数が正確に確定していない状態です。

つまり、未知なる物質が出てきて、その物質を構成している原子の数がよく分かっていない状況から始めて、まずは組成式だけでも確定させるという計算問題が出題されます。

たとえ何億もの原子の数でなくても、分からないところから始めて、最小の繰り返しの固まりを見つけたいという考えが大切になります。

そこで、ここからは典型的な有機化学の計算の練習問題を通して組成式と式量について説明をします。

高校の数学で鍛えている考察力や計算力と似たような力で頑張る内容となります。

※ 次の練習問題は計算のしやすさを狙って意図的に数字を設定しています。

実際の実験データではないのでご了承ください。

組成式 – 式量 :計算問題

【練習問題】

有機化合物 X が102mgあったとします。

ただし、X を構成している原子は C, H, O の 3 種類に限定されているとします。

この X を完全燃焼させると、
H₂O水54mgと
CO₂二酸化炭素264mgとなったとします。

このとき、X の組成式と式量を求めてください。

この手の問題を計算するときに、有機化合物 X の分子式が確定していないので、化学反応式を正確に把握することができません。

係数比がモル比となっているという計算ができないので、この単元ならではのアプローチを習得しなければなりません。

ただ、全てが新しいというわけでなく、中学の理科で学習した内容も役に立ちます。

反応前は X が102mgです。

反応後に水54mgと264mgの二酸化炭素の合計の質量が増えています。

これは、空気中の酸素が結びついたための質量の増加です。

中学の理科で学習した有機化合物が完全燃焼して水と二酸化炭素が生じるという内容です。

分子量が確定していないので、モル計算ができませんが、質量を足掛かりにして組成式を導き出します。

このときに、反応前後での X 以外からの原子の数（質量）の増加は空気中からの O 原子だけになります。

他の原子は加わっていないので、中学生のときから知っているラボアジエの法則から、反応前後で C 原子の数と H 原子の数に変化なしです。

ここから突破口を開きます。

HとCから質量を確認する

H₂O = 18 と水分子の分子量は分かっています。

この 18 のうち H 原子 2 個が占めるのは 2 です。

このことから、発生した水54mgのうち、2/18が H 原子全体の質量と考えられます。

つまり、54×2/18 = 6 (mg) が反応後の H 原子全体の質量の合計値です。

H 原子について、反応前後で数の変化はないため、反応前の H 原子全体の合計値も同じ値となっています。

つまり、完全燃焼する前の X に含まれていた H の質量は 6mgです。

同じ要領で X を構成している C 原子全体の質量を求めます。

CO₂ = 44 という分子量のうち、C 原子が占めるのは 12/44 です。

そのため、発生した264mgの二酸化炭素のうち、C 原子全体の質量の合計値が計算できます。

264×12/44 = 72 (mg) です。

C 原子についても、反応前後で原子の数が変化していません。

そのため、72mgという反応後の C 原子の質量の合計値が、そのまま反応前の燃焼する前の X に含まれている C 原子全体の質量の合計です。

O原子の質量は引き算で計算

O 原子の数については、X に含まれているものと空気中の酸素が結びついた分の２手があるわけです。

そのため、O の質量については先ほどの割合の計算をしませんでした。

しかし、C, H, O から成る X 102mgについて、H 原子全体の質量合計6mgと C 原子全体の質量合計72mgが分かっています。

よって、X に含まれている O 原子全体の質量合計は、
102－(6+72) = 24 (mg) です。

分かった X の内訳の内容をまとめます。

ここで注意点ですが、組成式についての原子の数の比ですが、これはモル比になっています。

そのため、求めた質量合計をそれぞれのモルに換算します。

C 原子は、12で割り、
72/12×10^-3モルです。

H 原子は、1 で割り、
6/1×10^-3モルです。

O 原子は、16で割り、
24/16×10^-3モルです。

これで、C : H : O を整数比で表すと組成式になります。

どの項にも10^-3が掛けられているので、一斉に簡単にできます。

そのため、
C : H : O
= 72/12 : 6/1 : 24/16
= 6 : 6 : 3/2
= 4 : 4 : 1 です。

すなわち、C₄H₄O が有機化合物 X の組成式です。

そして、
12×4+1×4+16
= 68 が求める式量です。

この練習問題を計算するにあたって、発生した水と二酸化炭素の質量が与えられていました。

これらを求めるための実験についての内容もテストで出題されることが多いので、簡単に述べておきます。

実験について

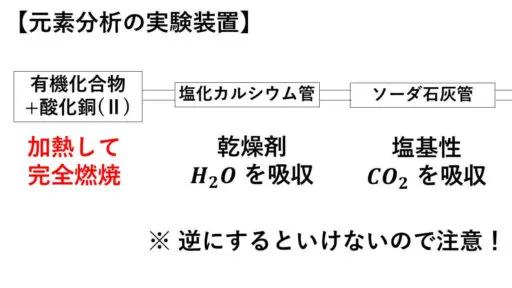
先ほどの計算問題で、発生した水と二酸化炭素の質量が与えられていました。

塩化カルシウムが乾燥剤として働くので、塩化カルシウム管のところで水が吸収されます。

そのため、この質量の増加が発生した水の質量というわけです。

先ほどの計算問題で54mgとなっていた数字は、ここから得られた数字という設定です。

発生した酸性の二酸化炭素については、塩基性のソーダ石灰のところで吸収します。

ソーダ石灰管のところで264mgの二酸化炭素の質量が増加したという設定でした。

この実験装置では、酸化銅(II)とともに加熱されます。

これは、酸化剤として働き完全燃焼させるために入れています。

有機化合物が不完全燃焼すると、COという一酸化炭素も発生し、どこにも吸収されずに出ていってしまいます。

そのため、COの C 原子の分だけ、X に含まれている C 原子が減少してしまって正しく計算ができなくなってしまいます。

そうならないように、完全燃焼させるために酸化銅(II)を入れて加熱しています。

逆にしてはいけない

【実験の注意】

加熱してから先に塩化カルシウム管を通し、その後でソーダ石灰管を通さなければなりません。

これを逆にしてしまうと正しいデータが得られなくなってしまいます。

なぜソーダ石灰管を先にすると、ダメなのかを説明します。

ソーダ石灰は塩基性で発生したCO₂を吸収しますが、乾燥剤でもあり、発生した水も吸収してしまいます。

そうなると、CO₂とH₂Oが混ざった形で質量が増加することになります。

こうなると、どちらの分の質量が、どれだけ増加したのか不明になってしまいます。

H₂OとCO₂の質量を合わせて318mg増加したとなってしまうと、上で述べた割合を使った計算ができなくなってしまいます。

そのため、H₂OとCO₂を別々に分けて、まずは吸収したH₂Oの分だけ質量が54mgだけ増加し、そして次に吸収したCO₂が264mgだけ増加したようにするわけです。

発生したH₂OとCO₂のそれぞれの質量の値を正確に把握するための実験なので、塩化カルシウム管とソーダ石灰管の順番を逆にしてはいけないということになります。

【他の記事】

■ モル濃度
■ ラウールの法則

他の理科の記事も投稿しています。

数学の記事を多く投稿しているサイトになりまして、次のような高校数学の記事も投稿しています。

■ 三乗和の公式（因数分解）
■ 二重根号の外し方

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。