16進数 – 変換 | アルファベットとの対応を桁の重みと合わせて理解
" 16進数 – 変換 “についてアルファベットがどの10進数の値に対応しているのかというところから解説しています。
桁の重みを押さえることで、アルファベットを他の進数の値へと置き換えることができます。
基礎的な知識と練習で、高校の数学と合わせて、情報の授業でよく出てくる16進数の変換のやり方を習得することができます。
16ずつで繰り上がりが起きる16進数です。
まず、10進数とのつながりを把握し、徐々に2進数とのつながりを押さえます。
16進数 :基礎となる知識
60進数だと60ずつで繰り上がりが起きます。
時計だと時間の単位があるので、理解がしやすいです。
59秒の次の60秒が1分へと繰り上がります。
ところが、コンピュータ関連で16進数を使うときに、秒のような単位がありません。
10進数の16に対応するところで繰り上がりが起きるのですが、10や11に対応する16進数は、まだ繰り上がりが起きていません。
繰り上がりが起きていないときに、1つの記号で10や11に対応する数を表すということを考えます。
そこで、アルファベットの A から F を使います。
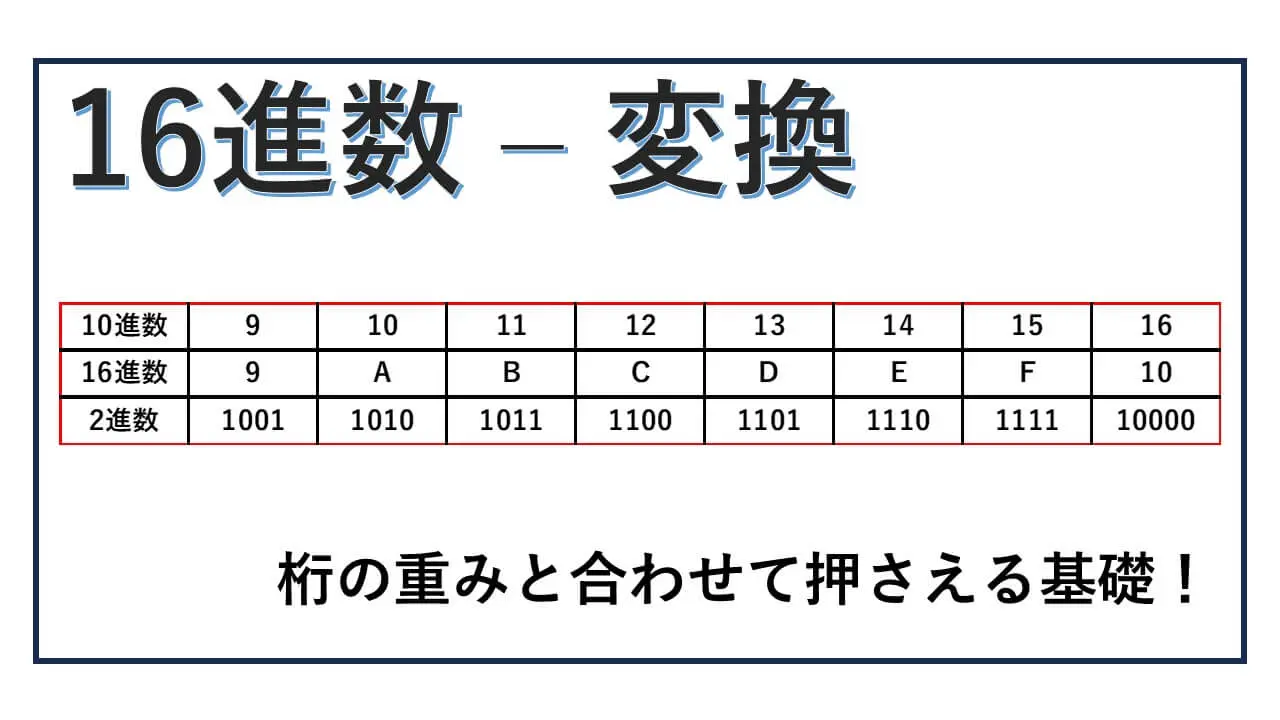
10進数の 0 から 9 のそれぞれに16進数の0(16)から9(16)が対応します。
ここから、アルファベットの出番です。
10進数では、9 の次が繰り上がって 10 ですが、16進数では9(16)の次で繰り上がりが起きていません。
なるべく少ない記号で表したいので、10進数の10に対応する16進数を A と表すというわけです。
16進数との対応を順に述べておきます。
10 – A(16), 11 – B(16),
12 – C(16), 13 – D(16),
14 – E(16), 15 – F(16) となります。
15という10進数に対応する16進数は、まだ繰り上がりが起きていないので、F と1つの記号で表しています。
そして、10進数の 16 に対応する数が、16進数では10(16)となります。
17 – 11(16), 18 – 12(16),
19 – 13(16), 20 – 14(16),
21 – 15(16), 22 – 16(16),
23 – 17(16), 24 – 18(16),
25 – 19(16), 26 – 1A(16),
27 – 1B(16), 28 – 1C(16),
29 – 1D(16), 30 – 1E(16),
31 – 1F(16), 32 – 20(16) となります。
33 だと 21(16)です。
桁の重みを考える
4ビットで考えているときは、
□163+△162+■161+◆160 という形で10進数の数字を表し、係数を左から順に並べると16進数の数となります。
□△■◆(16) が対応する16進数です。
33 という10進数の数を16進数へと変換してみます。
33 = 2×16+1 は、
0・163+0・162+2・161+1・160 です。
そのため、
0021(16) が 33 に対応する16進数となります。
ここで、160の係数が10から15までの二桁の10進数となっているときには、先ほどのアルファベットを使います。
10 – A(16) から 15 – F(16) という対応でした。
例えば、28 という 10進数に対応する16進数を求めてみます。
28 = 1×161+12×160 です。
12 – C(16) なので、
1C(16) が対応する16進数です。
4ビットで表しておくと、
001C(16) が10進数の28に対応する値です。
163 = 4096, 162 = 256 を利用して、もう少し大きな数で練習しておきます。
【練習問題】
4380 という10進数に対応する16進数を求めてください。
<解答と解説>
算数で学習したように、4380 の中に4096 が 1 個あって、残りが284 です。
さらに、284 の中に 256 が 1 個あり、残りが 28 です。
そして、28 の中に 16 があり、残りは 12 です。
この内容を数学の等式で表します。
4380 = 4096+284
= 1・163+284
= 1・163+1・162+28
= 1・163+1・162+1・161+12・160 となります。
160の係数が 12 と二桁なので、アルファベットも使います。
12 – C(16) なので、
111C(16) が対応する16進数となります。
10 – A(16) という対応規則だけを押さえておくと、11とB(16)などと順に15とF(16)までの対応が得られます。
160の係数が二桁のときにも、落ち着いてアルファベットへ置き換えれば円滑に変換することができます。
アルファベットを4桁で
コンピュータは 0 と 1 で認識します。
そのために、2進数が使われているということでした。
しかし、2進数だと、すぐに大きな桁になってしまうので、人が読みずらくなってしまいます。
そこで、16進数を導入することで、見やすくできます。
先ほど 10進数と16進数の変換を桁の重みについて説明しました。
同じ要領で、16進数のアルファベットを2進数へと置き換えることを考えます。
A(16) – 10 が対応だったので、10進数の 10 を2進数で表すことを考えます。
2の指数乗を使って、桁の重みを考えると 10 が2進数へと置き換わります。
10 = 8+2
= 1・23+0・22+1・21+0・20
= 1010(2) です。
※ 2進数という記事でも、2進数についての論点を解説しています。
これで、
A(16) – 10 – 1010(2) という対応が得られました。
後は順にずらすことで、アルファベットを2進数へと変換できます。
B(16) – 11 – 1011(2),
C(16) – 12 – 1100(2),
D(16) – 13 – 1101(2),
E(16) – 14 – 1110(2),
F(16) – 15 – 1111(2) という対応になっています。
高校の数学の指数の計算も合わせると、
10000(2)
= 24 = 16
= 0・163+0・162+1・161+0・160
= 0010(16) とつながっていることが分かります。
ここからは、16進数と2進数の直接の変換についてのやり方を解説します。
8ビットでB7(16) に対応する2進数を求めてみます。
16進数 : 変換
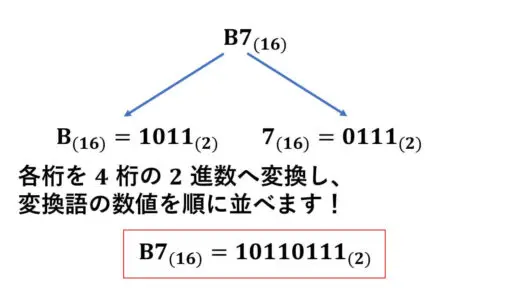
16進数から2進数へ変換するときは、1つの16進数を4桁の2進数へ置き換えます。
B7(16)だと、B(16)を4桁の2進数に置き換え、7(16)も2進数へ置き換え、その順に並べます。
先ほど説明したように、
B(16) = 1011(2) です。
この 1011 を左側の4桁とします。
7(16) は10進数の 7 に対応しています。
※ 0 から 9 までの10進数の数字は16進数でも同じです。10 以降で A からのアルファベットが登場していました。
7 = 0×8+1×4+1×2+1×1
= 0・23+1・22+1・21+1・20
= 0111(2) です。
これを右側の4桁とします。
合わせると、
10110111(2) がB7(16)に対応する2進数の値ということになります。
ちなみに、4桁の2進数ですが、最高位の数字が 1 のときにアルファベットの16進数と対応しています。
1010(2) が A(16)で、順にずらしてF(16)までが得られました。
1011(2) – B(16),
・・・
1111(2) – F(16) です。
これらを暗記するというより、規則に基づいて順に追えるようになっておくと、情報の授業のテストのときに心強いかと思います。
逆に2進数を16進数に変換するときは、今と反対の流れで置き換えをすることになります。
逆の作業の流れで変換する
【練習問題】
01111011(2)を16進数へ変換してください。
<解答と解説>
左から順に4桁ずつに分け、各々を16進数へ変換すれば完了です。
0111(2) と 1011(2) に分かれます。
0111(2)は最高位の数が 1 でないため、アルファベットではないということが分かります。
2進数を桁の重みを考えて10進数にすると、その数がそのまま16進数ということになります。
0111(2)だから、
0・23+1・22+1・21+1・20
= 1×4+1×2+1×1
= 4+2+1 = 7 です。
このように0111(2)が10進数の 7 に対応していることが、計算をするとすぐに分かります。
7 はまだ繰り上がっていないので、16進数でも7(16)です。
これで、
0111(2)を7(16)に変換するということが分かりました。
今度は、1011(2)を16進数へ変換します。
最高位の位の数が 1 なので、アルファベットになるという心積もりをしておきます。
1・23+1・21+1・20
= 8+2+1
= 11 です。
そのため、10進数の11が対応しています。
10 – A(16) という対応でしたから、もう1つだけずらします。
10進数の10と16進数のB(16)が対応しています。
よって、
1011(2)にB(16)が対応していることが分かりました。
それぞれ変換した後の16進数を合わせます。
7B(16)が、
01111011(2)に対応している16進数ということになります。
この練習問題では、8桁なのでちょうど4桁と4桁に分かれました。
桁が足りないときには、一番左の4桁に 0 を補って表示させます。
0を付け足すとき
110101(2)を16進数に変換することを考えます。
下の位から4桁に区切り、足りないところに 0 を付け足します。
11(2) と 0101(2) に分かれるので、
11(2)に 0 を付け加え、
0011(2) と 0101(2) に分かれていると考えるわけです。
どちらも最高位が 0 なので、アルファベットが出てこないということが分かります。
0011(2)は、
2+1 = 3 なので、3(16)です。
0101(2)は、
8+1=9 なので、9(16)です。
順に合わせると、
39(16) ということになります。
110101(2)と2進数だけで考えていると大きな桁ですが、16進数を使うと39(16)と少ない桁数で表せるというわけです。
今回は高校の数学と情報に関わる内容を述べました。
情報量-ビットという情報の授業に関連する記事を投稿しています。
また、トレミーの定理といった高校の数学についての記事も投稿しています。
それでは、これで、このブログ記事を終了します。
読んで頂き、ありがとうございました。