トレミーの定理 – 証明 | 比について外項の積と内項の積が等しいことを利用
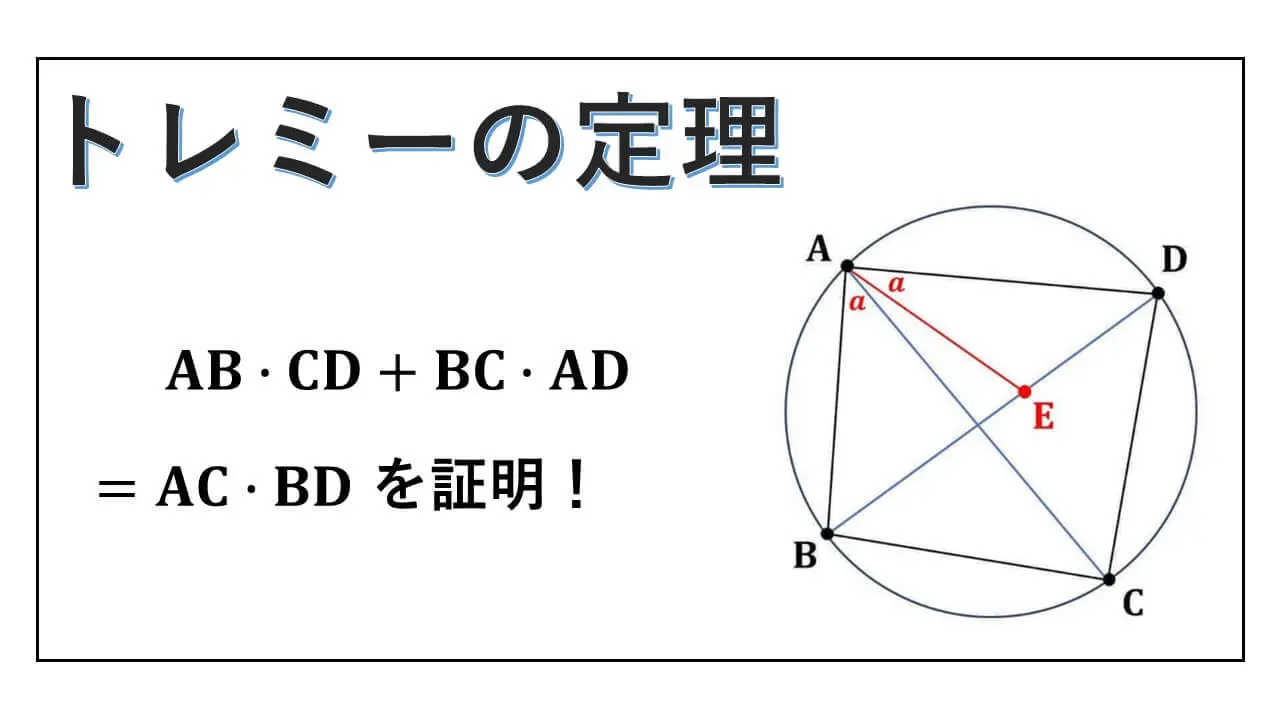
" トレミーの定理 “の証明について述べています。
円に内接する四角形ABCD について、向い合う辺の長さの積どうしで和を取ると、対角線の長さどうしの積となるという定理です。
つまり、
AB・CD+BC・DA
= AC・BD ということになります。
結果は覚えやすい形ですが、平面図形に関して、与えられた線分の長さたちの四則演算で得られる値についての証明問題が出題されることがあります。
そういった証明問題の練習として、トレミーの定理は良いトレーニングとなります。
なお、この記事で述べる四角形は、どの内角も 180°未満の大きさのものとして議論を進めています。
トレミーの定理 – 証明 :相似比の利用
【問題１】
円に内接する四角形ABCDが与えられたとします。
ただし、この四角形は、どの内角も 180°よりも小さいとします。
さらに、∠EAD = ∠BAC となるように点 E が対角線BD 上に取れたとします。
このとき、次の (1), (2), (3) を示してください。
＜証明＞
(1) を三角形の相似を利用して、示します。
△AED と △ABC について、
仮定より、
∠EAD = ∠BAC です。
また、
弧AB に対する円周角より、
∠ADE = ∠ACB です。
よって、
２組の角がそれぞれ等しいので、
△AED ∽ △ABC となっています。
これから、相似比を利用して、(1) の等式を導きます。
(1) に使われている値が外項の積と内項の積に現れるように、相似な三角形を探し、それを証明しておいたというわけです。
外項の積と内項の積
△AED ∽ △ABC より、
AD : DE = AC : CB です。
外項の積と内項の積が等しいので、
CB = BC だから、
BC・AD = AC・DE です。
これで、(1) の等式が導けました。
(2) の等式も相似な三角形を利用して導きます。
△ABE ∽ △ACD を示します。
∠ABE = ∠BAC+∠EAC です。
また、仮定より、
∠DAC = ∠EAD+∠EAC
= ∠BAC+∠EAC です。
すなわち、
∠ABE = ∠DAC です。
さらに、
弧AD に対する円周角より、
∠ABE = ∠ACD です。
よって、
２組の角がそれぞれ等しいので、
△ABE ∽ △ACD です。
ゆえに、
AB : BE = AC : CD となっています。
外項の積と内項の積が等しいので、
AB・CD = AC・BE です。
これで、(2) の等式も導けました。
線分BDの長さが100%
点 E は線分BD の内分点となっています。
そのため、
BE+DE = BD です。
先ほどの図を見ると当たり前の事実ですが、この書き換えを使うことで、(3) の等式が得られます。
(1) より、
BC・AD = AC・DE,
(2) より、
AB・CD = AC・BE でした。
これらの等式を辺々足すと、
AB・CD+BC・AD
= AC・DE+AC・BE
= AC・(DE+BE)
= AC・(BE+DE)
= AC・BD となります。
これで、(3) が得られました。【証明完了】
この (3) がトレミーの定理の結論の等式です。
この【問題１】では、
∠EAD = ∠BAC となるように点 E が対角線BD 上に取れたという設定のもとで議論をしました。
状況によっては、
∠BAD－∠BAC が∠BAC よりも小さくなってしまうこともあります。
そこで、そのような状況でトレミーの定理を証明するという問題が出題されることを想定して、次の【問題３】についても述べておきます。
ちなみに、
∠BAD－∠BAC = ∠BAC のとき、
つまり、AC が∠BAD の二等分線となっているときは、【問題１】のときよりも簡単な状況になっています。
図を描くと、
△AED ∽ △ABC,
△ABE ∽ △ACD が、すぐに分かります。
そのため、【問題１】と同じ計算でトレミーの定理が成立していることが分かります。
これについては、【問題２】として先に証明を述べておきます。
トレミーの定理 :他の場合について
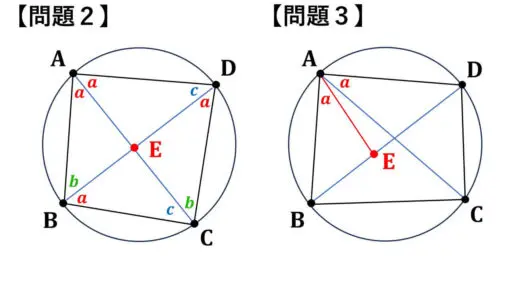
【問題３】は、∠BAE = ∠CAD となるように点 E が対角線BD 上に取れた場合についてです。
【問題２】は、
２組の角がそれぞれ等しいため
△AED ∽ △ABC,
△ABE ∽ △ACD となり、【問題１】と同様の比の計算をすると定理が成立します。
そのため、【問題３】の方について解説します。
△ABE ∽ △ACD,
△ABC ∽ △AED を示すことになります。
△ABE と △ACD について
∠BAE = ∠CAD であり、
弧AD に関する円周角より
∠ABE = ∠ACD です。
これで、△ABE ∽ △ACD となります。
そのため、
AB : BE = AC : CD です。
外項の積と内項の積が等しいため、
AB・CD = AC・BE …(1)
次に、△ABC と △AED について相似の証明を行います。
∠BAC = ∠BAE+∠EAC
= ∠CAD+∠EAC
= ∠EAD となっています。
つまり、
∠BAC = ∠EAD です。
また、弧AB に関する円周角より、
∠ACB = ∠ADE です。
これで、
△ABC ∽ △AED が示せました。
そのため、
BC : CA = ED : DA です。
外項の積と内項の積が等しいため、
BC・DA = CA・ED …(2)
これらから、トレミーの定理の定理である向かい合う辺の長さの積どうしの和が対角線の長さの積となることを導きます。
辺々足すと
(1) より、
AB・CD = AC・BE,
(2) より、
BC・DA = CA・ED でした。
辺々足し合わせます。
そのときに、
BE+ED = BD ということを使います。
すなわち、
AB・CD+BC・DA
= AC・BE+CA・ED
= AC・BE+AC・ED
= AC・(BE+ED)
= AC・BD 【証明完了】
これで、起こり得るすべての場合について、トレミーの定理を示すことができました。
次は、この定理を使う練習問題になります。
定理を使う練習問題
【問題】
円に内接する四角形ABCDが与えられたとします。
AB = p, BC = x, CD = x,
DA = q, AC = p, BD = q という長さとします。
このとき、
1/p + 1/q = 1/x となることを証明してください。
四角形の４つの辺の長さと２本の対角線の長さが与えられているという状況です。
円に内接しているので、トレミーの定理を使えます。
トレミーの定理より、
AB・CD+BC・DA
= AC・BD となっています。
与えられている線分の長さを当てはめると次のようになります。
すなわち、
px+xq = pq という等式が成立しています。
ここで、線分の長さは正の実数なので、逆数をとることができます。
pqx > 0 より、1/pqx も 0 より大きい実数です。
1/pqx を成立している等式の両辺に掛けます。
すると、
1/q + 1/p = 1/x となります。
加法についての交換法則から、
1/p + 1/q = 1/x です。
これで、示したい結論が導けました。
定理から導かれる等式を変形したものが、この問題で示したかった等式というわけです。
今回は、高一の平面図形の内容について述べました。
関連する高校数学の平面図形の記事として、三角形の面積比という記事を投稿しています。
この記事ではチェバの定理を証明しています。
高校の論理を中学の内容を使って解説するという趣旨の記事として、トレミーの定理のように対角線が関連するひし形という記事を投稿しています。
また、方べきの定理についても解説をしています。
ここで、今回のタロウ岩井の記事を終了します。
読んで頂き、ありがとうございました。