ひし形 – 定義 | 4つの辺の長さがすべて等しい四角形【面積の公式も】
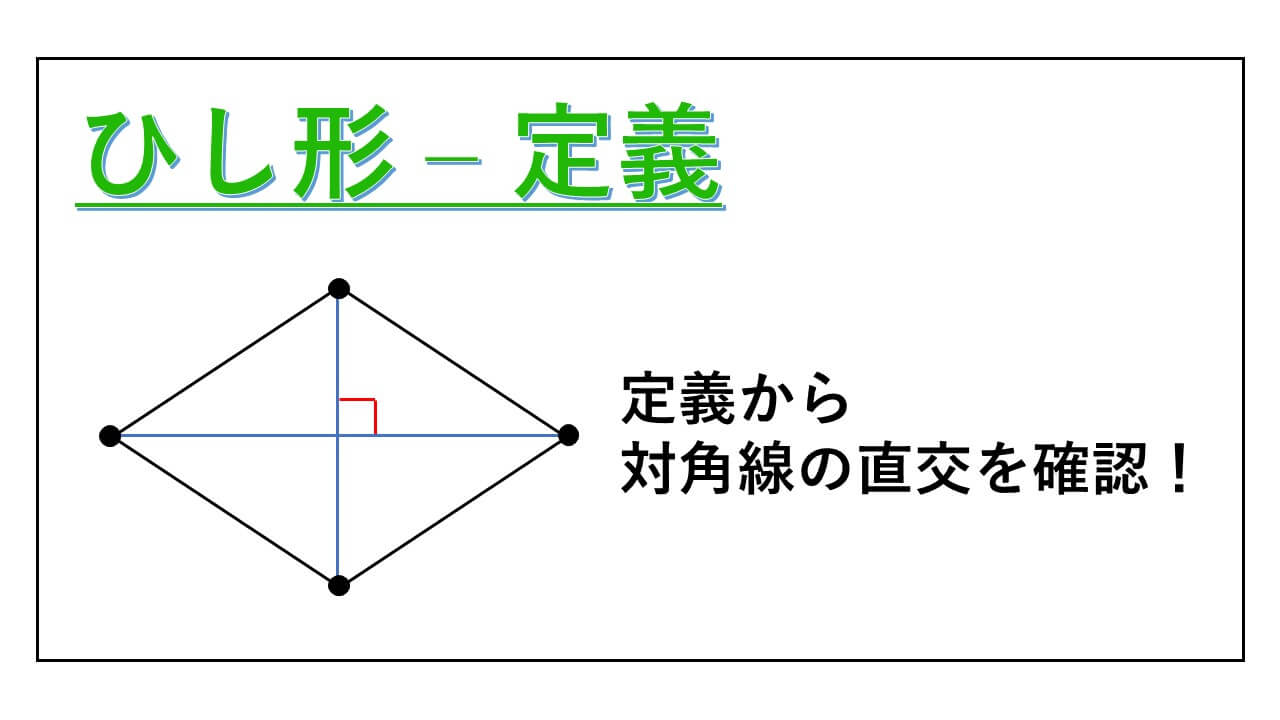
" ひし形 “の「 定義 」は、4つの辺がすべて等しい四角形です。
中学の数学で学習したひし形を使って、高校で扱われる論理について解説をしています。
また、ひし形の定義から、その対角線が直角に交わっていることを導きます。
既に知っている事実を使うことで、数学の論理へのハードルを下げ、その分、論理の内容に集中することを目的として、この記事を投稿しました。
また、この記事の後半では、ひし形の面積を求める公式を示しています。
論理と合わせて客観的な計算による考察の練習になれば幸いです。
ひし形 : 定義 から考察を始めて
【定義】
4つの辺の長さがすべて等しい四角形をひし形という。
この定義から論理的に推論を進めて、ひし形について成立する正しい(真である)命題を導きます。
ひし形についての命題として、その2本の対角線が垂直に交わるということが挙げられます。
ひし形の定義から、2本の対角線が直交しているということを導くために、数学の論理の流れを考えることが大切になります。
そこで使う数学の論理ですが、「既に証明されている正しい命題を使えるときには使って良い」という推論規則を使います。
「使えるときには使う」ということですから、使う前に使える状況であることを確かめておく必要があります。
今回、ひし形の対角線が直交するという命題を証明するために使う既に証明された命題たちを述べておきます。
【平行四辺形であるための条件】
平行四辺形について、次の条件①から⑤は、どの二つも必要十分条件である。
① 向かい合う2組の辺はそれぞれ平行である。
対角線が中点で交わる四角形より
② 向かい合う2組の辺の長さはそれぞれ等しい。
③ 向かい合う2組の角の大きさはそれぞれ等しい。
④ 対角線がそれぞれの中点で交わる。
⑤ 1組の向かい合う辺が等しく平行である。
条件①が平行四辺形であることの定義です。
すべて必要十分条件(同値)なので、四角形が一つでも条件を満たすと、平行四辺形であるための定義を満たし、平行四辺形ということになります。
そして、平行四辺形については、どの条件も満たしているということになります。
では、この平行四辺形であるための条件を使って、ひし形についての命題を証明します。
その前に、すぐに偽(正しくない)と断定できる命題について述べておきます。
「四角形について、その2本の対角線が垂直に交わっているならば、ひし形である」という命題は偽です。
偽である理由は、仮定条件を満たすけれども、結論条件を満たさない四角形の例(反例)が存在するからです。
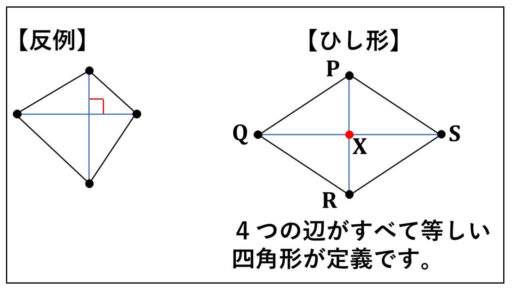
図より、2本の対角線が垂直に交わっていますが、4つの辺の長さがすべて等しくない(ひし形の定義を満たさない)四角形が存在します。
このように、反例が存在すると命題が偽ということになります。
※ 補集合-差集合という記事で、この内容を集合を用いて解説しています。
1つの命題が偽であったとしても、その逆が真ということも起こり得ます。
それでは、次に正しいと証明できる命題を扱います。
対角線の直交を確認
【命題1】
四角形PQRS が与えられたとする。
このとき、四角形PQRS がひし形であるならば、その2本の対角線が垂直に交わる。
<証明>
対角線PR と対角線QS を引き、交点を X と置きます。
△PQX と △PSX が合同であることを示します。
仮定より、四角形PQRS はひし形なので、4つの辺の長さがすべて等しい四角形です。
そのため、平行四辺形であるための条件②を満たすため、四角形PQRS は平行四辺形です。
平行四辺形だから、④より、対角線がそれぞれの中点で交わっています。
よって、
QX = SX …(1)
また、共通の辺より、
PX ~ PX …(2)
さらに、ひし形の定義から、
PQ = PS …(3)
(1), (2), (3) から、3組の辺の長さがそれぞれ等しいため、△PQX と △PSX は合同です。
合同な三角形の対応する角の大きさが等しいため、
∠PXQ = ∠PXS です。
そして、3点 Q, X, S が同じ直線上の点なので、
∠PXQ + ∠PXS = 90° です。
∠PXS に ∠PXQ を代入すると、
2∠PXQ = 180° です。
両辺を 2 で割ると、
∠PXQ = 90° です。
これは、対角線PR と対角線QS が直交していることを示しています。【証明完了】
この【命題1】の証明では、「ひし形ならば平行四辺形」ということで、平行四辺形が与えられていることから、平行四辺形について既に成立している命題を使いました。
このように、既に証明された命題が使える状況だと、その命題を使うことができます。
このような推論の流れを考えることが高校以降の数学で大切になります。
ちなみに、先ほど述べたように、【命題1】の逆は、反例が存在するため偽となっています。
今度は、ひし形の面積についての命題を証明します。
数学の論理と合わせて、客観的な計算によって得られた値も考慮に入れる内容となっています。
ひし形 – 定義 :面積の公式
【命題2】
ひし形PQRS が与えられたとし、その面積を a とする。
このとき、
a = PR × QS ÷ 2 である。
<証明>
対角線PR と対角線QS の交点を X と置きます。
仮定より、四角形PQRS がひし形なので、【命題1】から、PR と QS は垂直に交わっています。
そのため、
a = △PQS+△RSQ
= QS×PX÷2+QS×RX÷2
…★となっています。
ここで、÷2 は 1/2 を掛けることなので、★の右辺を乗法の式に直すことができます。
つまり、
QS×PX÷2+QS×RX÷2
= QS×PX×1/2+QS×RX×1/2
この右辺を因数分解します。
すると、
QS×PX×1/2+QS×RX×1/2
= QS×(PX+RX)×1/2 です。
×1/2 にしたことで、乗法についての結合法則と分配法則を用いて因数分解をすることができました。
さらに、PX+RX は対角線PR の長さです。
そのため、
QS×(PX+RX)×1/2
= QS×PR×1/2 です。
これが★の右辺の値です。
よって、
a = QS×PR×1/2 です。
乗法についての結合法則と交換法則から、
a = PR×QS×1/2 です。
×1/2 を ÷2 に戻すと、
a = PR × QS ÷ 2 です。【証明完了】
このように、論理の流れと計算規則を考慮に入れることで、数学の証明をすることが多いです。
この【命題2】を証明するときにも、既に証明をした【命題1】を適用しました。
そのため、ひし形ということから、2本の対角線が垂直に交わっているということが使えたわけです。
ちなみに、この結論の式を導くときに、四角形の対角線が垂直に交わっているということが本質的に効果を発揮していました。
そこで、【命題2】は、次の【命題3】へと一般化できます。
より一般化した命題
【命題3】
2本の対角線が垂直に交わっている四角形PQRS が与えられたとし、その面積を a とする。
このとき、
a = PR × QS ÷ 2 である。
<証明>
対角線PR と対角線QS の交点を X と置きます。
仮定より、PR と QS は垂直に交わっています。
そのため、
a = △PQS+△RSQ
= QS×PX÷2+QS×RX÷2
…★となっています。
これで、【命題2】の証明の途中と全く同じ状況になりました。
後は、全く同じ証明をすると、結論の等式が導けます。
実際に、証明を記述してみます。
★の右辺を乗法の式に直すと、
QS×PX÷2+QS×RX÷2
= QS×PX×1/2+QS×RX×1/2
因数分解をすると、
QS×PX×1/2+QS×RX×1/2
= QS×(PX+RX)×1/2 です。
PX+RX は対角線PR の長さなので、
QS×(PX+RX)×1/2
= QS×PR×1/2 です。
これが★の右辺の値です。
よって、
a = QS×PR×1/2 です。
乗法についての結合法則と交換法則から、
a = PR×QS×1/2 です。
×1/2 を ÷2 に戻すと、
a = PR × QS ÷ 2 です。【証明完了】
【命題2】の証明で、「ひし形だから対角線が垂直に交わっている」としたことが、【命題3】では仮定として満足されていました。
そのため、同様の証明ができたというわけです。
【命題3】の証明をすべて述べましたが、高校の数学だと、同様にして成立と述べられたりもします。
関連する記事について
三角形の面積について、高校では様々なアプローチがなされます。
平面図形について、三角形の面積比という記事で、チェバの定理を証明しています。
また、三角比とベクトルを合わせた内容について、ヘロンの公式という記事を投稿しています。
四角形の対角線に関しては、
トレミーの定理について解説をしています。
中学で学習した図形を使って、高校の論理をトレーニングするという記事で、平行四辺形-定義という記事も投稿しています。
高校の数学では、論理と集合を使って考察を進めることがあります。
共通部分 和集合という記事で、そのような内容の基礎について解説をしています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。