一般線形群 | 中心を求める【特殊線形群の中心も一緒に考察】

2023年9月5日

「 一般線形群 」は、可換体 K の元を成分とする n 次正方行列で行列式が 0（K の零元）でないものをすべて集めた集合 G(n, K) に、行列の乗法で二項演算を定めた群です。

この記事では、体 K は乗法について可換である可換体として議論を進めます。

A と B について、det A と det B が 0 でないとき、
det AB = (det A)(det B) なので、
det AB は 0 でありません。

そのため、G(n, K) は、行列の乗法で閉じています。

線形代数で学習したように、行列式が 0 でないということは、逆行列をもつ（可逆である）ことと同値です。

A∈G(n, K) について、
det A^-1 = (det A)^-1 です。
※ (det A)^-1 は det A∈K の K における乗法逆元のことです。
※ 一般の可換体 K がややこしいと思われるときは、実数体と思って読み進めて頂いて差しつかえありません。

また、n 次の単位行列の行列式も 0 でなく、行列の乗法についての結合律から、G(n, K) は群の定義を満たします。

この群を一般線形群といい、G(n, K) と表します。

体 K 上の n 次正方行列で行列式が 0 でない（可逆である）ものをすべて集めた群ということです。

この記事では、G(n, K) の中心を求めることを主眼に解説しています。

以下では、n を 2 以上の自然数として議論を進めます。

一般線形群 :特殊線形群も一緒に考える

M(n, K) という記号で、体 K の元を成分とする n 次正方行列全体を表すことにします。

そして、K の加法単位元を 0、乗法単位元を 1 と表すことにします。

そして、対角成分が全て 1∈K である単位行列を E と表すことにします。

{A∈M(n, K) | det A ≠ 0} が、
一般線形群 G(n, K) です。

{X∈G(n, K) det X = 1} という一般線形群の部分集合を、
SL(n, K) と表すことにします。

部分群の判定方法から、SL(n, K) が一般線形群の部分群となっていることが分かります。

実際、X, Y∈SL(n, K) とすると、
det XY^-1 = (det X)(det Y)^-1

この右辺は、1, 1^-1∈K の積なので、
det XY^-1 ≠ 0 です。

この SL(n, K) という G(n, K) の部分群を特殊線形群といいます。

さらに、正規部分群であることも分かります。

A∈G(n, K), X∈SL(n, K) に対して、
det (AXA-1) =
= (det A)(det X)(det A)^-1 です。

体 K は可換体なので、
(det A)(det X)(det A)^-1
= (det X)(det A)(det A)^-1
= det X = 1

そのため、AXA^-1∈SL(n, K) より、正規部分群ということになります。

中心を求めるための行列

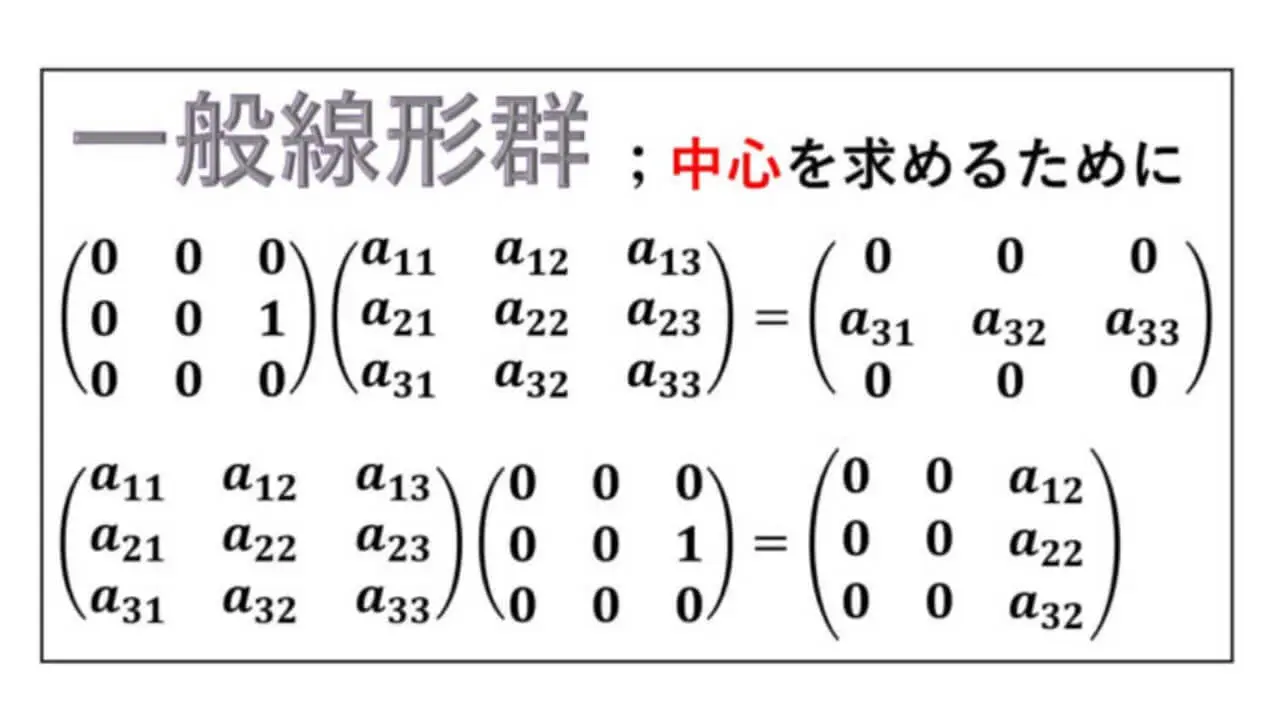
s, t を 1 以上 n 以下の自然数とします。

E_s,t を (s, t) 成分が 1∈K で、他の成分が全て 0∈K である n 次正方行列とします。この正方行列を行列単位といいます。

E_s,t (s, t = 1, … , n) という n² 個の行列が、M(n, K) を体 K 上のベクトル空間と考えたときの基底となっています。

n が 2 以上の自然数であるとき、
det E_s,t を s 行以外の行で余因子展開すると、値が 0 と分かります。

※ 余因子展開について、リンク先のnote記事で具体的な行列について求め方を解説しています。

ここで、s ≠ t のときを考えます。

一方、行列式の性質から、
det (E+E_s,t) は、
s 列の －1 倍 を t 列に加えても値は変わりません。

s 列の －1 倍 を t 列に加えると、単位行列の行列式です。

したがって、
det (E+E_s,t) = det E = 1 です。

このことから、
s ≠ t のとき、
E+E_s,t∈SL(n, K) となっています。

この行列を利用して、G(n, K) の中心を求めます。

一般線形群 :中心を求める方針

{A∈G(n, K) | AB = BA (∀B∈G(n, K))} が一般線形群の中心です。

Z(G(n, K)) で一般線形群の中心を表すことにします。

{αE | α∈K, α ≠ 0} という部分群に含まれる任意の行列は、G(n, K) の中心に含まれています。

実は、Z(G(n, K)) のどの元も、この部分群に含まれることが、行列計算から導かれます。

Z(G(n, K)) から任意に行列 A をとると、A は G(n, K) の任意の行列と乗法について可換です。

特に、SL(n, K) の任意の行列と可換です。

s ≠ t のとき、
E+E_s,t∈SL(n, K) だったので、
A(E+E_s,t) = (E+E_s,t)A です。

分配律で括弧を外して整理すると、
M(n, K) において、
AE_s,t = E_s,tA … ★

1 以上 n 以下の自然数 s, t で、
s ≠ t を満たす 1 つの組 (s, t) について、★が成立しています。

そのため、n²－n 通りの (s, t) について、
★の等式が成立しています。

この行列単位との積について、各成分を比較すると、次のことが分かります。

【命題】

n を 2 以上の自然数とし、s, t は n 以下の自然数で、s ≠ t とする。

また、A = (a_i,j) が、
AE_s,t = E_s,tA を満たすとする。

このとき、a_ss = a_tt,
a_s1, … , a_ss-1, a_ss+1, … , a_sn は全て 0 である。

ただし、s = 1 のときは、
a₁₂, a₁₃, … , a_1n が全て 0 である。

この命題が成立していると、一般線形群と特殊線形群の中心を求めることができます。

この【命題】を使うと、次のような考察をすることができます。

t = 1 で s を 2 以上 n 以下の自然数とすると、
a_ss = a₁₁ となります。

そのため、(a_ij) = A∈Z(G(n, K)) の対角成分の値は、すべて a₁₁ と等しくなっています。

また、s = 1 から s = n までのそれぞれについて【命題】を適用すると、A の対角成分以外が全て 0 ということになります。

そのため、A = a₁₁E (a₁₁∈K) となります。

det A = (a₁₁)ⁿ で、
A∈G(n, K) より、det A ≠ 0 です。

体 K は整域なので、
(a₁₁)ⁿ ≠ 0 より、a₁₁ ≠ 0 です。

よって、A = a₁₁E (a₁₁∈K) は、
{αE | α∈K, α ≠ 0} に含まれます。

以上の内容から、
Z(G(n, K)) は、
{αE | α∈K, α ≠ 0} に一致します。

特殊線形群についても同様に

Z(SL(n, K)) を特殊線形群の中心とします。

X = (x_ij) を Z(SL(n, K)) の任意の行列とします。

1 以上 n 以下の自然数 s, t で、
s ≠ t のとき、
E+E_s,t∈SL(n, K) でした。

そのため、X は E+E_s,t と可換になります。

そのため、一般線形群のときと同様に、
XE_s,t = E_s,tX となります。

よって、X も【命題】の仮定を満たすことになります。

したがって、同様の考察から、
X = x₁₁E となります。

x₁₁E は G(n, K) の任意の行列と可換なので、
X = x₁₁E∈Z(G(n, K)) となります。

すなわち、
Z(SL(n, K)) ⊂ Z(G(n, K)) です。

これより、
Z(SL(n, K)) =
SL(n, K) ∩ Z(G(n, K)) となります。

これは、特殊線形群の中心に含まれる行列は、一般線形群の中心に含まれていて行列式の値が 1 である行列ということです。

群の中心は、正規部分群になっているので、剰余群を定義することができます。

剰余群 SL(n, K)/Z(SL(n, K)) を
PSL(n, K) と表し n 次射影特殊線形群といいます。

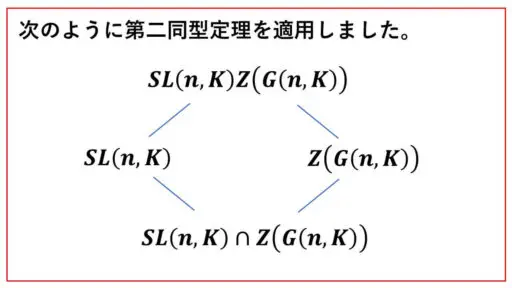
ここで、SL(n, K) は G(n, K) の正規部分群だったので、第二同型定理より、
SL(n, K)/SL(n, K)∩Z(G(n, K) は、
SL(n, K)Z(G(n, K))/Z(G(n, K)) と群として同型になります。

すなわち、
PSL(n, K) は、
SL(n, K)Z(G(n, K))/Z(G(n, K)) と群として同型です。

G(n, K)/Z(G(n, K)) を、
PG(n, K) と表し、n 次射影線形群といいます。

SL(n, K)Z(G(n, K))/Z(G(n, K)) は、
G(n, K)/Z(G(n, K)) の正規部分群なので、
同型対応で同一視を使って、
PSL(n, K) を PG(n, K) の正規部分群と見なされるときもあります。

それでは、証明を飛ばしていた【命題】の証明をします。

一般線形群 :行列の乗法の定義から

n ≧ 2 で、s ≠ t のとき、
A = (a_i,j) が、AE_s,t = E_s,tA を満たしていると、
a_ss = a_tt,
a_s1, … , a_ss-1, a_ss+1, … , a_sn は全て 0 であることを証明します。

ただし、s = 1 のときは、
a₁₂, a₁₃, … , a_1n が全て 0 です。

＜証明＞

E_s,t の (α, β) 成分を e_αβ と表すことにします。
(α, β) = (s, t) のとき (s, t) 成分の値が 1 で、他の成分は全て 0 になっています。

AE_s,t の (i, j) 成分の値は、
Σ_k a_ike_kj です。

j ≠ t のときは、e_kt = 0 なので、
Σ_k a_ike_kj = 0 です。

そのため、AE_s,t は、t 列以外の各列は、どの成分も 0 となっています。

j = t のとき、
k は 1 から n まで動き、s は n 以下の自然数なので、k の値が s となるときがあります。

e_sj = e_st = 1 以外は全て 0 なので、
Σ_k a_ike_kj = a_is です。

ゆえに、AE_s,t の (i, t) 成分は、a_is となっています
（i = 1, 2, … , n）。

つまり、AE_s,t の t 列は次のようになっています。

(1, t) 成分 a_1s,
(2, t) 成分 a_2s,
・・・
(s, t) 成分 a_ss,
・・・
(n, t) 成分 a_ns … (1)

今度は、E_s,tA の (i, j) 成分の値である
Σ_k e_ika_kj を調べます。

i ≠ s のときは、e_ik = 0 なので、
Σ_k e_ika_kj = 0 です。

E_s,tA は s 行以外の各行の成分は 0 となっています。

i = s のときを考えます。

(s, j) 成分の値は次のようになります。

e_st 以外は全て 0 なので、
k = t 以外の項の値は 0 より
Σ_k e_ska_kj = a_tj です。

ゆえに、
E_s,tA の s 行は、
(s, 1) 成分から (s, n) 成分まで順に
a_t1, a_t2, … , a_ts, … , a_tn
… (2) となっています。

AE_s,t = E_s,tA で、
s ≠ t なので、
この積である行列は、
t 列以外のどの列も成分が 0 で、
s 行以外のどの行も成分が 0 です。

そして、(1) と (2) より、
t 列と s 行がクロスする (s, t) 成分の値以外は、どの成分も 0 ということになります。

AE_s,t = E_s,tA の (s, t) 成分を比較すると、
a_ss = a_tt です。

AEs,t の t 列 について、
(s, t) 成分以外の t 列の値は全て 0 です。

そのため、(1) から、
s = 1 の場合、
a₁₂, a₁₃, … , a_1n が全て 0 です。

s ≧ 2 の場合、
a_s1, … , a_ss-1, a_ss+1, … , a_sn は全て 0 です。【証明完了】

ここまで、一般線形群や特殊線形群の中心を考えました。

良い活躍をしたのが行列単位 E_s,t でした。

最後に、行列単位について復習をしておきます。

行列単位について

M(n, K) という K の元を成分とする n 次正方行列全体は、行列の加法と K からのスカラー倍について、K 上のベクトル空間の公理を満たしています。

そして、このベクトル空間の基底を構成するのが行列単位です。

E_i,j (i, j = 1, … , n) という n² 個の行列単位が基底となっています。

M(n, K) は n² 次元の有限次ベクトル空間であり、さらに行列の乗法を考えることで、結合律を満たす結合代数となっています。

任意のベクトルは、基底の一次結合で一意的に表すことができるということを直和の記号を用いて表しておきます。

E_i,j で生成されている 1 次元の部分空間を KE_i,j と表します。

M(n, K) = ⊕_i,j KE_i,j と、直和空間の直和に分解しています。

今回は、乗法について、この行列単位との積がどうなっているのかということを押さえ、その結果を足掛かりに議論を進めました。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。