可解群 | 定義の同値な書き換えと、p群などで具体的な考察をする練習

2023年8月16日

" 可解群 " の定義には、同値な書き換えがあります。

群論の入門内容で学習する同値な書き換え内容を把握した上で、可解群についての基礎的な命題を証明します。

また、p 群が可解であることや位数 p²q の群が可解であることを途中の考察する過程を示して証明します。

その際には、群の共役作用についての内容を使います。

この記事では、群 G の単位元のことを e と表すことにします。

可解群 :定義と同値な書き換え

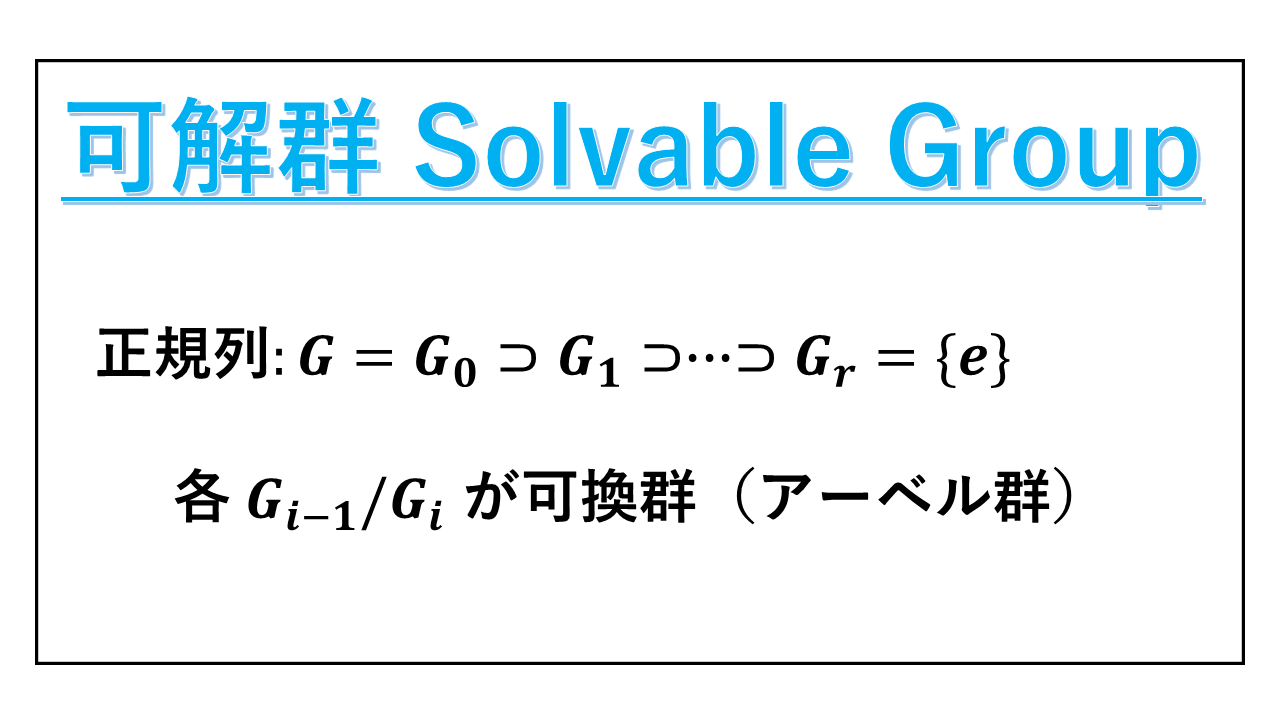
【可解群の定義】

G を群とする。

G = G₀ ⊃ G₁ ⊃ … ⊃ G_n = {e} という正規列で、各剰余群 G_i-1/G_i が可換群（アーベル群）となっているものが存在するとき、G を可解群と定義する。

この可解群の定義には、同値な書き換えがあります。

まず、組成列に関連する書き換えです。

【同値な書き換え１】

有限群 G が可解群であることの必要十分条件は、G の組成因子が全て素数位数の群であることである。

ブログ組成列より

この証明は、リンク先の記事で述べています。

また、その記事で、「群 G の正規部分群 N について、G/N と N が可解群であれば、G も可解群である」ことも示しています。

組成列に関連する書き換えと、この命題は、可解群を学習し始めるときに出てくる基本となる内容になります。

また、交換子群列を用いた可解群の定義の書き換えもあります。

【同値な書き換え２】

群 G が可解群であることと、ある自然数 r が存在して、長さ r の交換子群列が単位群となることが同値である。

ブログ交換子群より

この r 次の交換子群が単位群となるという書き換えも可解群を学習するときの基本となります。

この書き換えの証明や交換子群についての基本的な命題は、リンク先で証明しています。

有限群については、同値な書き換えが二つあることになるので、状況によって使いやすいもので可解群かどうかを判断することができます。

群 G が、G と 単位群以外に正規部分群をもたないとき、G を単純群といいます。

単純群が可解群だと、どういうことなのかを示す命題を証明します。

交換子群についての内容を使って、考察を進めます。

有限単純群が可解群なとき

G を位数が 2 以上の有限群とします。

G が単純群かつ可解群だとすると、G は素数位数の巡回群となります。

G が可解群なので、[G, G] という交換子群は、G に真に含まれることになります。

これは、[G, G] = G とすると、【定義の書き換え２】の内容に反することになるためです。同様に、可解群であることから、交換子群列は有限の長さで単位群に到達します。

ここで、G が可換群（アーベル群）でないとすると、
D₁(G) = [G, G] が {e} とは異なることになります。

一般に D₁(G) は G の正規部分群（そして、G/D₁(G) が可換群）であることから、
G ⊃ D₁(G) ⊃ {e} が正規列で、
D₁(G) は G や {e} と異なる正規部分群ということになります。

これは、G が単純群であるという仮定に矛盾します。

そのため、G は可換群でなければなりません。

よって、G の位数が素数位数でなければ、シローの定理から素数位数の真部分群が存在することになります。

今、G は可換群なので、どの部分群も G の正規部分群だから、G が単純群ということに反します。

したがって、G の位数は素数位数でなければなりません。

そして、素数位数の群は巡回群となっています。

これで、有限群 G が単純群であり、かつ可解群であるとき、G が素数位数の巡回群であることを示すことができました。 ■

この証明では、交換子群についての内容を使いました。状況によって、可解かどうかを判断しやすいものを使って考察を進めることになります。

可解群の部分群も可解

G を可解群とし、H を G の部分群とします。

G が可解群のとき、その部分群も可解群になっています。

仮定から、【同値な書き換え２】より、
G ⊃ D₁(G) ⊃ … ⊃ D_r(G) = {e} と、有限の長さで交換子群列が単位群に辿り着きます。

各 i 次の交換子群（導来群）について、
D_i+1(G) = [D_i(G), D_i(G)] は、
D_i+1(H) = [D_i(H), D_i(H)] を含みます。

そのため、
H ⊃ D₁(H) ⊃ … ⊃ D_r(H) = {e} と、有限の長さで交換子群列が単位群に到達します。

そのため、【同値な書き換え２】より、
H は可解群です。 ■

また、同じ要領で、可解群の剰余群も可解であることが分かります。

可解群 G の正規部分群を N とすると、
D_i(G/N) = D_i(G)/N なので、
ある自然数 r で、D_r(G) = {e} となるため、
D_r(G/N) = {N} となり、交換子群列が有限の長さで単位群となります。

そのため、G/N も可解群となります。

可解群の準同型像も可解

群 G から群 G’ への群準同型写像を f とします。

このとき、G が可解群であるとすると、f(G) も可解群です。

このことを証明します。

i = 1 のとき、
f(D₁(G)) = f([G, G])
= [f(G), f(G)] = D₁(f(G)) です。

これの繰り返しを考えます。正確に帰納法で示します。

自然数 i について、
f(D_i(G)) = D_i(f(G)) と仮定します。

すると、次のようになります。

これで、どの自然数 n についても、
f(D_n(G)) = D_n(f(G)) となることが帰納法によって示されました。

また、G が可解群であることから、ある自然数 r が存在して、
D_r(G) = {e} なので、
{f(e)} = f(D_r(G)) = D_r(f(G)) です。

f(e) は f(G) の単位元なので、f(G) の交換子群列は長さ r で単位群となるということになります。

これで、【同値な書き換え２】から、
f(G) も可解群です。 ■

次の内容は、シローの定理を中心に可解群となることを証明する練習問題です。

可解群 :位数2023の群は可解

位数 2023 = 17²× 7 の群は可解群になります。一般的な方が証明をしやすいときもありまして、位数 p²q （p と q は異なる素数）の群が可解群ということを証明します。

p群の中心という記事で、位数 p² の群は可換群ということを示していまして、これも証明で使います。

位数 p²q （p と q は異なる素数）の群 G は可解群である。

＜証明＞

シローの定理から、G にはシローp部分群 P が存在します。

{gPg^-1 | g∈G} という G の部分集合（シローp部分群）たちの集まりを S とします。

G から S への作用を共役作用で定義すると、S は P 軌道のみとなります。

ここで、P についての固定部分群は、P の正規化群 N_G(P) です。

N_G(P) = {g∈G | gPg^-1 = P} という G の部分群です。

よって、|S| = |G| ÷ |N_G(P)| です。

P は N_G(P) の部分群となっているので、ラグランジュの定理から、N_G(P) の位数は、p² 以上であり、G の位数の約数となっていることが分かります。

そのため、|S| は、1 か q のどちらかです。

【|S| = 1 の場合】

このとき、{gPg^-1 | g∈G} = {P} なので、P は G の正規部分群です。

G ⊃ P ⊃ {e} という正規列を考えると、
G/P は位数 q の群で、素数位数の群が巡回群ということから、可換です。

また、P の位数は p² なので、p群の中心が単位群でないというブログで示した通り、P は可換群です。

そのため、P と単位群で剰余群を作ると、P と同型なので、その剰余群も可換群です。

そのため、G ⊃ P ⊃ {e} という正規列は、可解群の定義を満たします。

【|S| = q の場合】

このとき、N_G(P) ≠ G なので、
p² ≦ |N_G(P)| < p²q です。

q が素数なので、p² より大きく p²q より小さい範囲に p²q の約数となる p² の倍数は存在しません。

ゆえに、|N_G(P)| = P² でなければなりません。

つまり、N_G(P) = P となっています。

シローの定理から、シローp部分群どおしは共役なので、シローp部分群の個数を t とすると、
t = |S| です。

そのため、t = |G|÷|N_G(P)| = q です。

ここで、シローの定理から、シローp部分群の個数 t = qは、
q－1 が p で割り切れます。

よって、q > p … (1)

今、シローq部分群を Q と置くと、
N_G(Q) = G または N_G(Q) ≠ G のいずれかです。

そこで、N_G(Q) ≠ G だと仮定して、矛盾を導きます。

このとき、シローq部分群全体を T と置くと、
T = {gQg^-1 | g∈G} で、
|T| = |G|÷|N_G(Q)| なので、
|T| は p または p² です。

さらに、|T|－1 は素数 q で割り切れます。

(1) より、p < q なので、
|T| = p だとすると、p－1 は q で割り切れません。

そのため、|T| = p² となります。

|T| = |G|÷|N_G(Q)| だったので、
|N_G(Q)| = |G|÷|T|
= p²q ÷ p² = q

さらに、Q ⊂ N_G(Q) ということから、
Q の位数が q なので、
Q = N_G(Q) となります。

これは、N_G(Q) ≠ G という仮定に矛盾です。

そのため、背理法から、
N_G(Q) = G です。

これで、Q が正規部分群ということが示せました。

そのため、
G ⊃ Q ⊃ {e} は正規列です。

さらに、剰余群 G/Q は位数 p² の群なので可換群です。

Q/{e} は Q に同型で、Q は素数位数の群なので、巡回群だから可換群です。

そのため、G ⊃ Q ⊃ {e} という正規列は、G が可解群であることの定義を満たします。

以上より、位数 p²q （p と q は異なる素数）の群が可解群ということを証明することができました。 ■

証明で用いた S は、シローp部分群全体で、シローの定理から、どのシローp部分群も共役作用について移り合います。

そのために、S が P を含む一つの軌道となっています。これを置換群の言葉で、遷移的 (transitive) といいます。

T については、Q を含む一つの軌道となっていて、やはり遷移的です。

有限群の有限な対象への作用の内容を用いて、可解かどうかを考える練習として、位数 p²q の群を取り挙げました。

これで、位数 2023 = 17²×7 の群は可解群ということが示せました。

可解群の定義と合わせて、指数2の部分群が正規部分群ということが、群論の入門で出てきます。

そのため、そのことを無限位数の群について示しておきます。

指数2の部分群は正規部分群

【命題１】

群 G の部分群を H とし、H の G における左剰余分解についての指数が 2 とする。

すなわち、
G = H ∪ aH (a ∈ G), H ∩ aH は空集合

このとき、H の G における右剰余分解について、
G = H ∪ Ha, H ∩ Ha は空集合となっている。

つまり、右剰余分解についての指数も 2 である。

この【命題１】を証明するために、左剰余類と右剰余類の定義を確認しておきます。

x ∈ G に対して、
{xg | g ∈ G} = xH が、x を含む H についての左剰余類です。

x, y ∈ G について、x^-1y ∈ H となっているときに、x ～ y と定義すると、この二項関係 ～ は、同値関係となっていています。

そして、x を含む同値類が、左剰余類 xH と一致しています。

また、x ∈ G について、
{gx | g ∈ G} = Hx が右剰余類です。

x, y ∈ G に対して、xy^-1 ∈ H となっているときに、二項関係 x ～’ y を定義すると、～’ は同値関係となっていて、x を含む同値類が Hx に一致しています。

これらの内容を用いて、論理的な考察を進めます。

右分解がどうなっているか

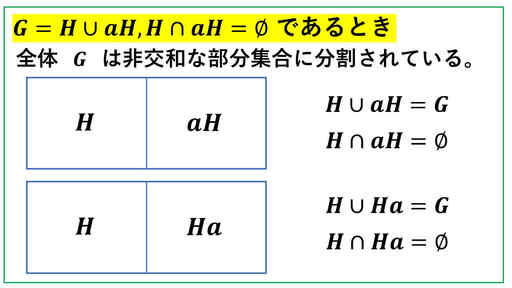
結論から述べますと、このベン図のようになっています。

どうして右剰余類も同じ指数 2 となっているのかを正確に理解しておくことが、後々の群論の理解に役立つかと思います。

感覚的に aH = Ha で H は正規部分群と思うと楽です。

しかし、学習し始めたときに、この手の内容を論理的に決定する思考力をトレーニングすることで、より複雑になった状況へと考察を進めていけるようになるかと思います。

【命題１】の仮定より、
G = H ∪ aH (a ∈ G) で、H と aH の共通部分が空集合ということでした。

a = ae ∈ aH なので、H と aH の共通部分が空集合だから、a は H に含まれいないということになります。
（a ∈ H だとすると、a が H と aH のどちらにも含まれることになり、H と aH の共通部分が空集合であることに反してしまいます。）

このような感じに、論理を使って考察を進めます。

今、与えられた a は H に含まれていないということが分かりました。

さらに、H ∩ Ha が空集合ということが、同様の考察から分かります。

ある x ∈ H ∩ Ha が存在したと仮定します。

すると、x ∈ Ha なので、
ある h ∈ H が存在して、
x = ha となります。

よって、xh^-1 = a です。

x, h ∈ H であり、H が部分群であることから、
xh^-1 ∈ H なので、a ∈ H となります。
※ 部分群の判定法という一つ前の記事で、部分群の定義の書き換えについて解説をしています。

これは、先ほど導いた a が H の元ではない G の元ということに矛盾します。

そのため、H ∩ Ha は空集合となります。

ここまでで、
H ∪ Ha ⊂ G,H ∩ Ha = Φ だと分かりました。

あとは、和集合が全体 G に一致していることを示せば、H の右剰余分解についての指数が 2 ということを示せたことになります。

Haがどこに含まれるか

今、G = H ∪ aH, H ∩ aH = Φ という左分解より、
aH = G － H …(★)

※ 差集合-補集合については、リンク先の記事で解説しています。

x ∈ G を任意にとります。

x ∈ H の場合、x ∈ H ∪ Ha^-1 となっています。

x が H に含まれていない場合を考えます。

このとき、x^-1 ∈ H とすると、x ∈ H となってしまうので、x^-1 ∈ aH となります。

そのため、
ある h ∈ H が存在し、x^-1 = ah

よって、x^-1 の逆元である x は、
x = (ah)^-1 = h^-1a^-1∈ Ha^-1

ゆえに、x ∈ H ∪ Ha^-1

したがって、G から任意にとった x について、x が H の元である場合でも、x が H の元でない場合でも x が、この和集合の元であることが示せました。

よって、G = H ∪ Ha^-1 となっています。

また、a は H の元ではないので、a^-1 も H の元ではありません。
（a^-1 ∈ H としてしまうと、逆元 a が H の元となってしまいます。）

よって、同値関係 ～’ についての同値類に関して、H ∩ Ha^-1 = Φ

よって、
G = H ∪ Ha^-1, H ∩ Ha^-1 = Φ

これより、Ha^-1 = G － H

(★) より、aH = Ha^-1

今、Ha ⊂ G = H ∪ aH であり、Ha と H の共通部分が空だったので、
Ha ⊂ aH = Ha^-1

いったん、ここまでの議論の帰結をまとめます。

指数2の部分群 :既に証明した命題の適用

【補題１】

群 G の部分群 H に対して、
G = H ∪ aH (a ∈ G), H ∩ aH = Φ だとすると、
G = H ∪ Ha^-1, H ∩ Ha^-1 = Φ となる。

逆元を用いての右分解の指数が 2 となっています。

論理的に既に証明した命題を適用することで、この記号を整備します。

G = H ∪ aH (a ∈ G) であり、 H と aH の共通部分が空集合だとします。

このとき、【補題１】より、
G = H ∪ Ha^-1,
H ∩ Ha^-1 = Φ

ここで、この a^-1 ∈ G なので、再び【補題１】の仮定を満たしています。

今、
G = H ∪ Ha^-1 (a^-1 ∈ G),
H ∩ Ha^-1 = Φ

ゆえに、【補題１】を再び適用すると、
G = H ∪ H(a-1)^-1 (a^-1 ∈ G),
H ∩ H(a^-1)^-1 = Φ

ここで、
(a^-1)^-1 = a なので、
G = H ∪ Ha (a ∈ G),
H ∩ Ha = Φ

これで、【命題１】の証明が完了できました。

この逆元が絡むループに気づかないと、G が有限群だという仮定が必要な気がしてしまいます。

命題の仮定は、緩い方が適用範囲が広がるので、できるだけ一般化した形で証明をしておきたいところです。

次に指数 2 の右分解が与えられたときに、同様に考察して、期待通りの結果を得られます。

右分解が与えられたとき

【命題２】

群 G の部分群 H について、
G = H ∪ Ha (a ∈ G), H ∩ Ha = Φ となっていたとき、
G = H ∪ aH, H ∩ aH = Φ

h ∈ H について、
(ha)^-1 = a^-1h なので、次の【補題２】が同様の考察で導けます。

この【命題２】の仮定を満たすと、a^-1 について、【補題２】の仮定を満たすので、【補題２】の結論が従います。

そのため、
G = H ∩ (a^-1)^-1H,
H ∩ (a^-1)^-1H = Φ

そして、(a^-1)^-1 = a なので、【命題２】の結論へ到達します。

形式的に指数 2 と書きましたが、G が無限群のときでも、有限群のときでも、上で述べた議論が使えます。

有限集合だと使えること

上の証明の中で、Ha ⊂ aH という状況から、二個の左剰余類に分解されていることから、逆元をクッションにして等しいことを導きました。

もし、G が有限群のときには、Ha と aH は G の部分集合なので、有限集合だから、すぐに等しいと分かります。

有限集合 S に含まれている元の個数を |S| と表すことにすると、次のようになります。

G が有限群のとき、任意の a ∈ G と、任意の部分群 H について、
|Ha| = |H| = |aH| となります。

このため、Ha ⊂ aH だと分かると、含まれている元の個数が同じことから、
Ha = aH となります。

|H|=|Ha|=|aH|の証明

H = {h₁, … , h_n} という有限個の元からなる 有限群 G の部分群だとします。

このとき、a ∈ G に対して、h_ia = h_ka だとすると、h^-1 を両辺に乗じて、h_i = h_k

この対偶をとると、
「h_i ≠ h_k ならば h_ia ≠ h_ka」となります。

したがって、
Ha = {h₁a, … , h_na} について、添え字が異なれば異なる元ということになり、含まれている元の個数は、H に含まれている元の個数と同じとなります。

|H| = |aH| についても同様の考察で、成立していることが分かります。

ちなみに、aH = Ha となっているとき、
aHa^-1 = H となります。

任意の g ∈ G に対して、gHg^-1 = H となっているときに、H を G の正規部分群といいます。

この定義と、ここまでで示したことを合わせると、次の定理となります。

関連する記事として、n次交代群という記事も投稿しています。

これで今回の記事を終了します。

読んで頂き、ありがとうございました。