表現行列 | 線形変換を行列表示する理論【右から行列を掛けることが線形変換を表す】

2022年1月2日

線形変換 (transformation) を表す「 行列表示 」について解説しています。表現された行列には、右から乗じるものと、左から乗じるものがあります。

どちらのタイプの行列でも線形変換を表現する流れは同じです。

そのため、右から掛ける行列に焦点を当て、具体例を通じて説明しています。

このブログ記事では、三次元について線形変換の行列表示について解説をしています。

n 次元でも同じ要領ですが、シグマ記号が煩雑になるので、三次元に絞っています。

表現行列 :線形変換を行列で表すために

有限次元の抽象ベクトル空間 V は、その次元を n とすると、1 行 n 列の行ベクトル全体と線形同型になります。

このことを利用することで、V から V への線形変換を、行列を使って表すことができます。

線形変換を行列表示することにより、行列に関する理論についての定理を適用することで、より多くの情報を引き出すことが期待できます。

また、行列を使うことで、状況を端的に表現することができることも魅力です。

この線形変換の行列表示について、一般の n 次元についてもやり方の本質は同じなので、3 次元のベクトル空間について、行列表示する方法を説明します。

3 次元だと、途中の一次結合をシグマ記号を使わずにすべて明確に記述できるので、線形代数学を学習し始めた方にとって、仕組みが見やすいかと思います。

※一般の n 次元になっても、シグマ記号を使うだけで、行列表示の仕組みの本質は同じです。

まず、行ベクトルに右から掛ける行列を求める方法を解説します。

そのために、有限次元ベクトル空間と線形同型な行ベクトルなベクトル空間についてから、説明をします。

線形同型写像で行ベクトルへ

Vを複素数体上の 3 次元ベクトル空間（線形代数）とします。

x, y, z ∈ V を V の基底を構成する 3 個のベクトルとします。基底を構成するベクトルの個数が、有限次元ベクトル空間の次元です。

実は、線形代数学の理論で、基底を構成するベクトルの個数は、そのベクトル空間において一定であることが証明されています。

※ 内積の定義という記事で、基底ベクトルの個数が一定であることの証明を解説しています。

v ∈ V を x, y, z の一次結合（線形結合）で表します。

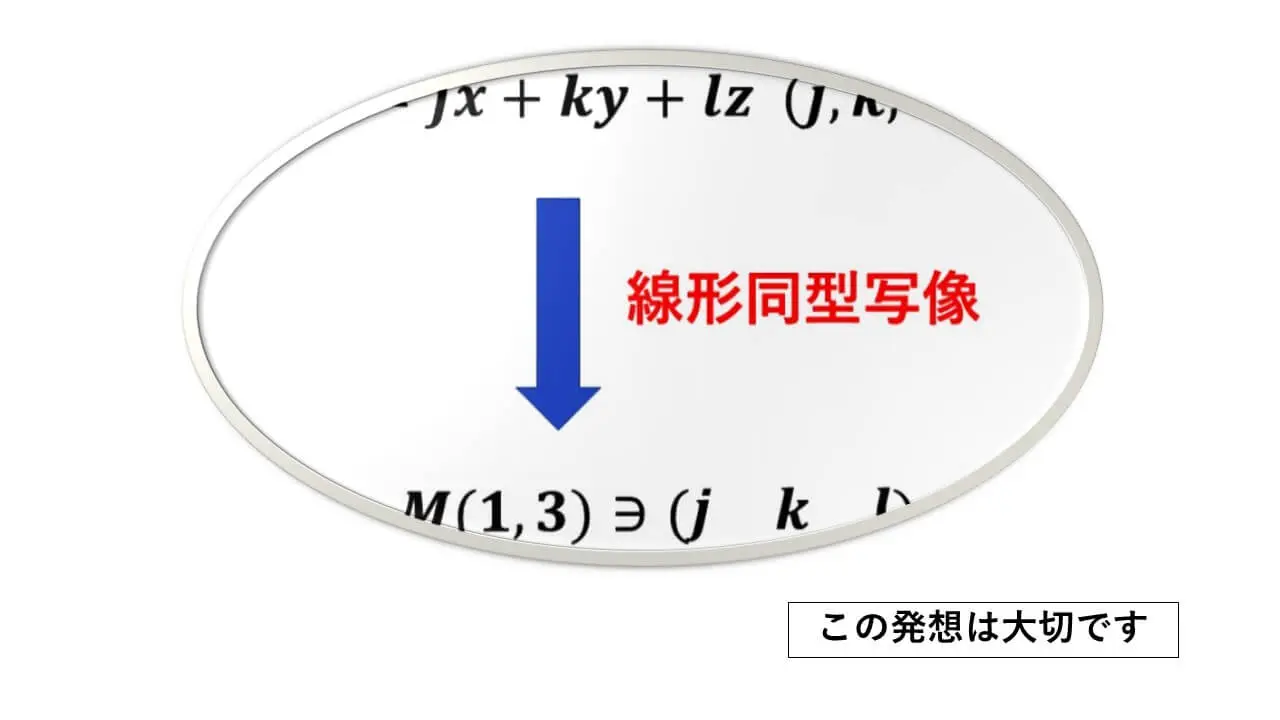
v = jx + ky + lz (j, k, lは複素数) のときに、次の対応によって、ベクトル空間 V は複素数を成分とする1行3列の行ベクトル全体 M(1, 3) と線形同型になります。

V ∋ v = jx + ky + lz (j, k, l ∈ C) となっているとき、
jx + ky + lz
↓ 線形同型
M(1, 3) ∋ (j k l) と対応させます。

基底を構成するベクトル x, y, z は一次独立なので、一次結合で V のベクトルを表す方法は、ただ一つです。

この一意性から、上述の対応が、写像の一対一対応として矛盾なく定義されていることが分かります。

x, y, zという3個の基底を構成するベクトルを固定し、g : V → M(1, 3) を、
g(v) = g(jx + ky + lz) = (j k l) と定めます。

この対応により、g は線形写像であり、かつ全単射となります。

これで、複素数体上の 3 次元ベクトル空間どおしの間に線形同型写像が定義されましたので、V と M(1, 3) の元どおしの対応がつきます。

fをVからVへの線形変換としたときに、v ∈ V の行き先である f(v) ∈ V がどのようになるのか。

これを M(1, 3) の元から M(1, 3) への対応で考えるということができます。

v と g(v)、f(v) と g(f(v)) の対応を見ることができるからです。

V においての動きを M(1, 3) における動きで考えることで、行列計算に落とし込んで計算ができるメリットがあります。

V のどの元についても、扱えるようにするために、基底を構成しているベクトルたちが、線形変換 f によって、どの V の元に移されているのかということを調べます。

まず、V の基底を構成している 3 つのベクトル x, y, z のそれぞれが、線形変換 f によって、f(x), f(y), f(z)に移されるときに、対応する行ベクトル g(f(x)), g(f(y)), g(f(z)) を、M(1, 3)において調べます。

V のどのベクトルも、基底の一次結合で一意的に表されます。

そのため、V のどのベクトルがどのように移されるのかが分かるようになります。

基底ベクトルに対応する行ベクトル

f(x) = a₁₁x + a₁₂y + a₁₃z　のときの対応です。

【V において】

x → f(x) = a₁₁x + a₁₂y + a₁₃z

【M(1, 3) において】

(1 0 0) に対して、
a₁₁(1 0 0)+a₁₂(0 1 0)+a₁₃(0 0 1) を対応

つまり、(1 0 0) → (a₁₁ a₁₂ a₁₃)

まず、基底を構成するベクトルxが、どうなるかを次のようにして確認します。

f(x) も、V のベクトルなので、x, y, z の一次結合で表すことができます。アルファベットの a と添え字を使って表しています。

x = 1x + 0y + 0z なので、x に線形同型な行ベクトルは、(1, 0, 0) となります。

同じく f(x) に対応する行ベクトルを考えると、M(1, 3) の元 (1, 0, 0) に対応する M(1, 3) の元が得られたことになります。

これが、上の図の一番下に書いている行ベクトルから行ベクトルへの対応です。

「x に対応する行ベクトルに対して、f(x) に対応する行ベクトルを対応させる」ということで、M(1, 3) から M(1, 3) への線形変換が定まります。

この行ベクトルから行ベクトルの対応について、次のように列ベクトルが絡んできます。

行と列が絡むので、行列の乗法を使って線形変換を表すということになります。

※なお、ここでいう列ベクトルとは、3 行 3 列の行列の 1 列目と 2 列目と 3 列目のことです。

表現行列 :右からの行列の乗法で

(1 0 0) という 1 行 3 列の行ベクトルに、
(a₁₁ a₁₂ a₁₃) という行ベクトルを対応させることを考えます。

この対応を行列の乗法で表すには、次のような行列の乗法を計算します。

A = (a_ij) という (i, j) 成分の値が a_ij となっている三次の正方行列を用意します。
（1 ≦ i ≦ 3, 1 ≦ j ≦ 3 です）

(1 0 0)A は、1×3 と 3×3 のサイズの行列の積なので、この行列の計算結果となる行列は、1 行 3 列の行ベクトルです。

そして、行列の乗法の定義から、各成分を計算できます。

(1, 1) 成分
1 × a₁₁ + 0 + 0 = a₁₁

(1, 2) 成分
0 + 1 × a₁₂ + 0 = a₁₂

(1, 3) 成分
0 + 0 + 1 × a₁₃ = a₁₃

すなわち、(1 0 0)A = (a₁₁ a₁₂ a₁₃)

これで、右から A を掛けると、
(1 0 0) に (a₁₁ a₁₂ a₁₃) を対応させるということになりました。

乗法の計算結果が、(1 0 0) という行ベクトルに対応する行ベクトルとなります。

残りの基底ベクトル (0 1 0) と (0 0 1) についても、同じようにして、f(y) と f(z) それぞれを x, y, z の一次結合で表します。

そのときに、現れるスカラー倍が計算結果となるように、行列を右から掛けます。今の段階で、その右から掛ける行列の 1 行目が出てきました。

f(x) を x, y, z の一次結合で表したときのスカラー倍の部分が使われています。

f(y)を一次結合で表したときには、同じくアルファベットのaを使い、添え字が「21」、「22」、「23」となるようにしています。

※ a₂₁, a₂₂, a₃₃ という f(y) を一次結合で表すときのスカラー倍のことです。

f(z)の一次結合の添え字は「31」、「32」、「33」としています。
※ f(z) = a₃₁x + a₃₂y + a₃₃z についての添え字のことです。

残りの基底ベクトルの行き先

y → f(y)=a₂₁x+a₂₂y+a₂₃z のときは、
右から掛ける行列の 2 行目が、
a₂₁ a₂₂ a₂₃ となっています。

先ほどと同じく、
(0 1 0)A = (a₂₁ a₂₂ a₂₃) ということが、行列の乗法の定義から分かります。

z → f(z)=a₃₁x+a₃₂y+a₃₃z のときは、
右から掛ける行列の 3 行目が、
a₃₁ a₃₂ a₃₃ となります。

やはり、(0 0 1)A = (a₃₁ a₃₂ a₃₃)

V における y → f(y), z → f(z) という対応を、行列の乗法によって表しました。

これで、基底を構成するベクトルが、それぞれ線形変換 f によって移されることを、行ベクトルと正方行列の乗法を使って表すための行列が得られました。

この行列を行ベクトルに右から掛けることで、線形変換による行き先に対応する行ベクトルが得られます。

今度は、一般の V の元 v について、f によって移されることを行列の乗法で表します。

ここまで当たり前のように使っていましたが、線形写像（線形変換）の定義を書いておきます。

【線形写像の定義】

V と W を複素数体上のベクトル空間とし、a, b を V の元とし、s と t を複素数とする。

このとき、
f : V → W が、
f(sa+tb) = sf(a)+tf(b) を満たせば、f を線形写像という。

線形変換は、始集合 V と終集合 W が同じベクトル空間のときの線形写像です。

この線形写像（線形変換）の定義を使って、v∈Vのfによる対応を、行列の乗法で表せることを確認します。

v = px + qy + rz (p, q, r は複素数) と、基底ベクトルの一次結合で表せたとします。

このとき、
f(v) = f(px + qy + rz) は、
pf(x) + qf(y) + rf(z) となります。

f(x), f(y), f(z) は先ほど行列の乗法で表しているので、そのときの行列が使えます。

対応関係に注意して、
pf(x) + qf(y) + rf(z) に対応する行ベクトルを書き出しみます。

任意のベクトルの行き先

V ∋ v = px + qy + rz の行き先は、
pf(x)+qf(y)+rf(z) ∈V

M(1, 3) ∋ (p q r) の行き先は、
pf(x)+qf(y)+rf(z) に対応する行ベクトルです。

p(a₁₁ a₁₂ a₁₃) + q (a₂₁ a₂₂ a₂₃) + r(a₃₁ a₃₂ a₃₃) という1 行 3 列の行ベクトルが対応します。

さらに計算したときの各成分です。

(1, 1) 成分
pa₁₁ + qa₂₁ + ra₃₁

(1, 2) 成分
pa₁₂ + qa₂₂ + ra₃₂

(1, 3) 成分
pa₁₃ + qa₂₃ + ra₃₃

f(x), f(y), f(z) のそれぞれに対応する行ベクトルは、先ほどの行列の1行目、2行目、3行目になっています。

したがって、v = px + qy + rz に対応する行ベクトル (p q r) の行き先となる行ベクトルは、このように計算できます。

最終的に、赤色で書いた値たちを成分とする 1 行 3 列の行ベクトルになります。

基底を構成するベクトルの行き先から作った行列を右から掛けると、f(v) に対応するこの行ベクトルが得られるのかどうかを確かめてみます。

A = (aij) として、
(p q r) という v に対応する行ベクトルに右から A を掛けます。

(p q r)A となります。

1 行 3 列の行ベクトルに右から3行3列の行列を掛けると、計算結果は 1 行 3 列の行列になります。

(1, 1) 成分
pa₁₁+qa₂₁+ra₃₁

(1, 2) 成分
pa₁₂+qa₂₂+ra₃₂

(1, 3) 成分
pa₁₃+qa₂₃+ra₃₃

これで、(p q r) に対応する行ベクトルを計算できました。これは、f(v) に対応する行ベクトルです。

これで、線形変換 f の V から V への対応を、行列を右から乗じることにより、 M(1, 3) から M(1, 3) への対応として扱えるようになりました。

ちなみに、この行列 A のことを、線形変換 f の表現行列といいます。後少し、細かい対応状況を正確に書いておきます。

右から掛ける表現行列のまとめ

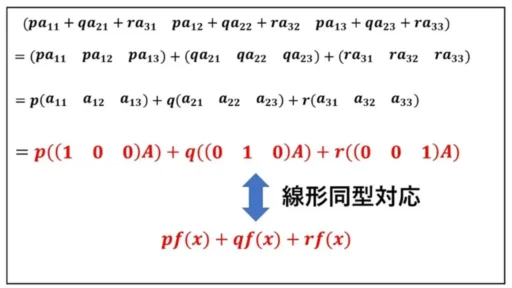
行ベクトルと行ベクトルの加法、そして複素数体から行ベクトルへのスカラー倍に注意して等しい関係をまとめておくと、図のようになっています。

ここまで押さえておくと、M(1, 3) において得られた行ベクトルが、V のどのベクトルと対応しているのかが明確に分かります。

※ ベクトル空間論で、線形変換に関連するのが不変部分空間についての内容です。

ベクトル空間についての学習を始めたときに、線形部分空間の定義を学習します。

その部分空間の定義に、線形変換についての条件が付け加わったものが不変部分空間の定義になります。

そのため、一気に関連する内容を押さえておくと良いかと思います。

【注意点】

抽象的なベクトル空間 V について、行ベクトルを対応させました。

V が、高校数学のベクトルで学習する平面ベクトルや空間ベクトルのように、はじめから行ベクトルになっているときがあります。

そのときは、行ベクトルのまま、基底の行き先を考えて表現行列を求められます。
※もとのベクトルと行ベクトルとの対応を省けるので、その分だけ楽になります。

状況によって、左から掛ける方が記述に適している、右から掛ける方が見やすいといった場面が分かれるかもしれません。

そのために、どちらでも扱えるようになっておくのが望ましいかと思われます。

表現行列を左から掛けるためには、Vのベクトルを列ベクトルに線形同型写像で移してから、さらに列ベクトルを列ベクトルに対応させる線形同型写像で移します。

左から列ベクトルに掛ける表現行列の求める方法は、一般次元について他の記事で述べることにします。

関連する行列の内容として、対角化という記事も投稿しています。

また、線形変換全体が環となっているということをEnd(V) という記事で確認しています。

他に、行列表示を使う例として、微分作用素という記事を投稿しています。

では、これで今回のブログ記事を終了します。

読んで頂き、ありがとうございました。