対角化 | やり方の理論を具体例で実践【理論の証明は区分された行列で】

2023年9月25日

" 対角化 “のやり方についての理論を用いて、具体的に行列の対角化を実践しています。

また、記事の後半で、その理論を区分された行列についての乗法の観点から証明しています。

適切に区分を設定することで、P^-1AP という行列の乗法を明確に把握し、理論の下支えの計算を見切ることが大切になります。

対角化の議論は、線形代数学の終盤の内容になり、既に学習した行列についての理論を使いながら、対角化についての新しい理論を構築することになります。

行列の各列から列ベクトルを作ったときに、それらの列ベクトルが線形独立であれば、行列の行列式が零でなく、逆行列をもつということも使います。

この記事では、複素数全体を C と表し、複素数を成分とする n 行 1 列の列ベクトル全体を Cⁿ と表すことにします。

また、記事の後半では、固有値についての基礎的な内容を述べています。

対角化 :理論の内容を理解する

V を複素数体 C 上の n 次元ベクトル空間とし、f を V から V への線形変換とします。

そして、f の行列表示を A とします。

A は複素数を成分とする n 次の正方行列となっています。

そして、A を n 次の列ベクトルに左から掛けることで、A は Cⁿ から Cⁿ への線形変換を引き起こします。

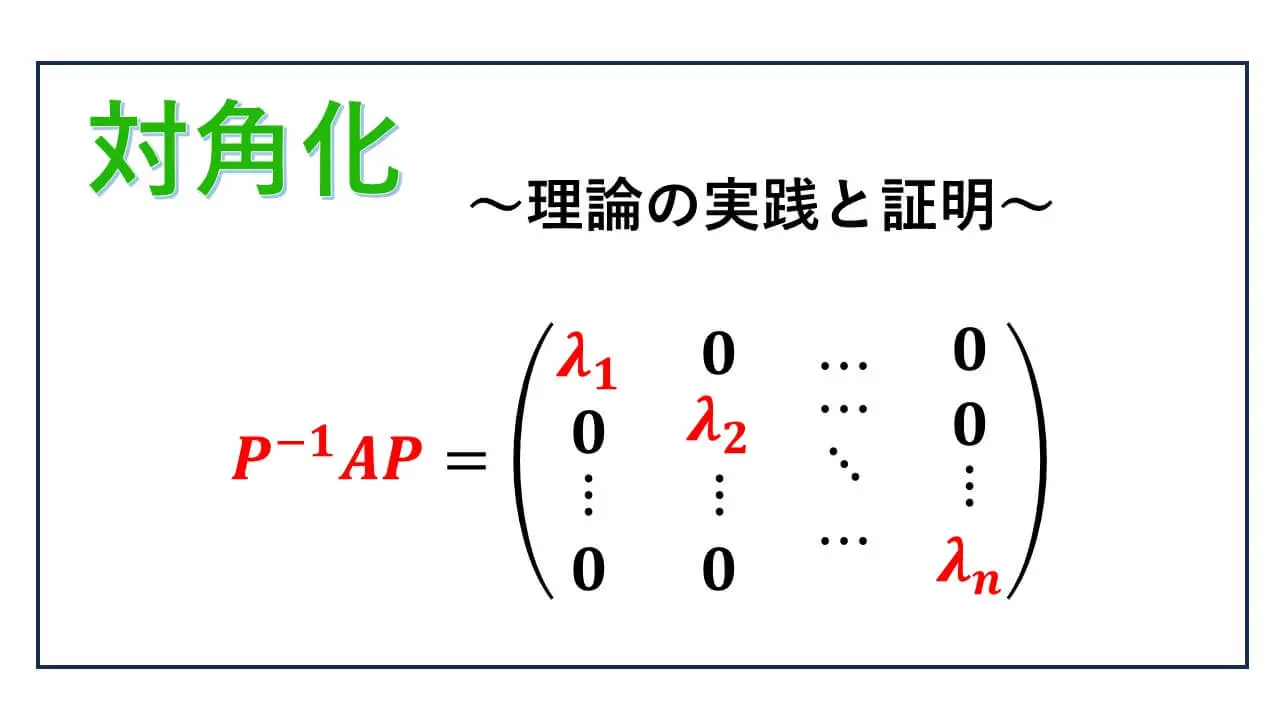
この内容を表現行列についての理論として学習しているわけですが、A をうまく変形して対角行列にしようというのが、対角化についての理論です。

u∈V－{0} を f で移したとき、
ある複素数 λ が存在して、
f(u) = λu となっているときに、u を固有値 λ についての固有ベクトルといいます。

p∈Cⁿ を、この u に対応する列ベクトルとすると、
Ap と列ベクトルに左から行列 A を掛けると、
Ap = λp となります。

※ 固有方程式を解くことで、固有値 λ が求まります。

このような、これまでに学習した内容を使って、さらに確実に対角化ができるときの理論を構築することを考えます。

その理論の一つとなる定理を、先に述べておきます。

対角化についての定理

λ₁, … , λ_n が A の相異なる固有値なので、それぞれについての固有ベクトル p₁, … , p_n は線形独立となっています。

※ 固有方程式という記事で、線形独立（一次独立）であることの証明を解説しています。

そのため、それらを 1 列目から n 列目まで並べた行列 P の行列式の値は零ではありません。

行列式の値が零でないことから、P は可逆（正則）ということになり、P は逆行列 P^-1 を持ちます。

学習の始めの段階で一般の n だと難しいので、n が 2 のときについて、この定理を具体的な例を通して使ってみます。

対角化 :具体例で理論を実践

複素数を成分とする 2 次正方行列を A とし、A の固有値を λ₁, λ₂ とします。

そして、λ₁, λ₂ についての固有ベクトルをそれぞれ p₁, p₂ とします。

次の図で述べている行列 A について、固有方程式を解き、λ₁, λ₂ をそれぞれ 2 と 5 としています。

2 次の固有ベクトル p₁, p₂ を求めておいて、それらを 1 列目と 2 列目に配置した行列を P と置きます。

これで、【定理】の条件が整いました。

実際に P^-1AP を計算すると、対角行列となっています。

対角成分に、はじめに与えられていた固有値が現れています。

理論と照らし合わせる

λ₁ = 2, λ₂ = 5 は相異なる固有値なので、固有ベクトル p₁, p₂ は計算しなくても線形独立となっていることが分かります。

また、P = (p₁ p₂) の各列についての列ベクトルが線形独立なので、P の行列式の値は零でないことが、行列式についての一般論から分かります。

そのため、逆行列 P^-1 が存在します。

P が具体的な比較的に扱いやすい行列なので、直接計算で P^-1 を求めることができます。

ただし、直接に P^-1 を求めなくても、
P^-1AP が (1, 1) 成分 λ₁, (2, 2) 成分 λ₂ の対角行列だと分かります。

これは、ブロック分割についての行列の乗法についての考え方です。

P^-1 の 1 行目から行ベクトル q₁ を作り、2 行目から行ベクトル q₂ を作ります。

すると、P^-1 は、q₁ と q₂ という 1 行 2 列の行列を区分行列として 1 列に配置した行列となっています。

P = (p₁ p₂) は 2 行 1 列の行列を区分行列としています。

適切に区分行列がセットされているので、P^-1P という行列の乗法をブロック分割を通して計算することができます。

単位行列を E とすると、P^-1P = E なので、
q₁p₁ = q₂p₂ = 1,
q₁p₂ = q₂p₁ = 0 と分かります。

q_ip_j は 1 行 2 列と 2 行 1 列の行列の積なので、1 行 1 列の行列となっています。

また、AP = (Ap₁, Ap₂) で、
Ap_i = λ_ip_i (i = 1, 2) だから、
AP = (Ap₁, Ap₂) = (λ₁p₁, λ₂p₂) となっています。

実際にブロック分割された行列を計算してみます。

理論の部分を n = 2 のときに確認しました。λ₁ と λ₂ はスカラーなので、複素数の乗法が可換なことから、スリ抜けてくれます。

一般の n 次正方行列についても、同様のブロック分割による計算で【定理】が証明できます。

対角化 :理論の証明

【定理】

A を複素数を成分とする n 次正方行列とし、λ₁, … , λ_n を A の相異なる固有値とする。

また、各 λ_i についての固有ベクトルを p_i∈Cⁿ とする。

このとき、
p₁, … , p_n を 1 列目から n 列目まで並べた行列を P とすると、P^-1AP は対角行列である。

＜証明＞

P = (p₁ p₂ … p_n) と n 個の列ベクトルに分割します。

p_j∈Cⁿ は固有値 λ_j についての固有ベクトルです。

λ₁, … , λ_n は A の相異なる固有値なので、
p₁, … , p_n が線形独立で、
|P| ≠ 0 より、P には逆行列 P^-1 が存在します。

P^-1 の i 行目を q_i という行ベクトルにして、ブロック分割をします。

q_i は 1 行 n 列、p_j は n 行 1 列の区分行列なので、
q_ip_j は 1 行 1 列の正方行列です。

そして、P^-1P = E より、
i ≠ j の場合、q_ip_j = 0,
i = j の場合、q_ip_j = 1 となっています。

AP = (Ap₁ Ap₂ … Ap_n)
= (λ₁p₁ λ₂p₂ … λ_np_n) です。

よって、P^-1(AP) が計算できます。

これで証明が完了しました。

n = 2 のときと同じブロック分割を使った行列の乗法の計算でした。

今回の記事では、複素数体上で議論を進めていたので、n 次の固有方程式が必ず解を持ちます。

細かいことを述べると、複素数体は代数学の基本定理により、n 次の複素係数の方程式は重解を含めて n 個の解をもちます。

しかし、実数体上での行列の話だと、n 次の固有方程式が虚数解を持ち、実数の範囲内では固有ベクトルが存在しないということが起こるときがあります。

そういったことまで考えると、対角化可能かどうかの議論が出てきますが、学習をし始めるときに、まずは n 個の固有値が相異なるという状況で、確実に対角化できるときの定理から勉強をすると良いかと思います。

次に、対角化された対角行列について、計算がしやすいことを示す内容を説明します。

対角行列のk乗

【命題】

A = (a_ij) を n 次の対角行列だとし、k を自然数とします。

このとき、A^k も対角行列で、
1 ≦ i ≦ n について (i, i) 成分の値は (a_ii)^k となっています。

＜証明＞

A は対角行列なので、対角成分でない成分の値は 0 となっています。

つまり、
i ≠ j のとき a_ij = 0 となっています。

A² = AA を行列の乗法の定義に基づいて、帰納法で示します。

A² の (s, t) 成分は、
a_s1a_1t+a_s2a_2t+…+a_sna_nt です。

ここで、
a_1t, a_2t, … , a_nt のうち、
a_tt 以外の値は 0 です。

そのため、
a_s1a_1t+a_s2a_2t+…+a_sna_nt
= a_sta_tt となっています。

s ≠ t のとき、
a_st = 0 なので、
(s, t) 成分の値は、
a_s1a_1t+a_s2a_2t+…+a_sna_nt
= a_sta_tt = 0 です。

これで A² の対角成分以外の成分の値がすべて 0 ということが分かりました。

次に s = t のときを考えます。

A² の (s, s) 成分の値は
a_s1a_1s+a_s2a_2s+…+a_sna_ns
= a_ssa_ss = (a_ss)² です。

これで、A² も対角行列で、
1 ≦ i ≦ n について (i, i) 成分の値は (a_ii)² となっていることが示せました。

繰り返しの操作について

k = p のとき、
A^p も対角行列で、
1 ≦ i ≦ n について (i, i) 成分の値は (a_ii)^p となっていると仮定します。

ここで、A^p の (s, t) 成分を b_s,t と置くことにします。

つまり、
s ≠ t のとき b_s,t = 0,
s = t のとき b_s,t = (a_ss)^p です。

A^p+1 = A^pA の (s, t) 成分は
b_s1a_1t+b_s2a_2t+…+b_sna_nt
= b_sta_tt となっています。

s ≠ t のとき、
b_st = 0 より、
A^p+1 = A^pA の (s, t) 成分は 0 です。

このため、A^p+1 は対角行列となっています。

今度は、s = t のときを考えます。

A^p+1 の (s, s) 成分は、
b_s1a_1t+b_s2a_2t+…+b_sna_nt
= b_ssa_ss
= (a_ss)^pa_ss
= (a_ss)^p+1 です。

これで k = p+1 のときにも成立していることが示せました。

帰納法より、任意の自然数 k について、命題が成立しています。【証明完了】

行列の対角化について、行列の乗法と定義とブロック分割、そして行列式についての理論を使いました。

対角化を通じて、行列についての理論を使う練習をしておくと、大学の数学科の今後の学習に役立ちます。

代数学で、群論を学習しますが、よく知られた群論の内容で行列が関連することがあります。

例えば、一般線形群について、基礎的なことを学習するときに、行列についての理論を使いながら群としての構造を考えます。

行列の計算についての理論を着実に押さえておくと、さらに代数学の理解を広げることができるので、n 次についての抽象的な証明に慣れておくと、その後に役立つ分野があります。

関連する記事として、
End(V)エンドモルフィズムという線形写像の成す環についての記事を投稿しています。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。