ネイピア数 | 定義と収束することの証明について【あの公理と同値なことが決め手】

ネイピア数 e を定義するために、収束する数列を使います。
高校数学の範囲で証明すべきことと、ネイピア数を定義するための数列が収束することについて、実数の連続性の公理が絡みます。
公理として認めているので収束するというのも一つの手ですが、実数の連続性の公理についてのことにも触れておきます。
an = (1+1/n)n が、ネイピア数の定義に使われる数列の一般項です。
この数列が、どうして収束するのかということについて、大学の数学で扱われる内容の詳細を他の記事で述べています。
高校の範囲で、数列 {an} が単調増加であり、上には限界がある(上に有界)ということまで証明します。
大学の数学で扱う内容を除くと、式の変形や不等式の評価について、大学受験で頻出となる内容が含まれているので、ネイピア数を定義する数列は、押さえておくと良いかと思います。
ネイピア数 :定義するための単調増加数列
an = (1+1/n)n を一般項とする数列 {an} が単調増加であることを示します。
単調増加とは、
a1 < a2 < … < an < an+1 < … となっているということです。
単調増加となっていることを示すときに、二項定理を使います。
※ シグマ記号という記事で、二項定理を証明しています。
a1 = 2, a2 = (3/2)2 = 9/4 = 2.25 なので、
a1 < a2 となっています。
n ≧ 2 のときについて、単調に増加していることを示します。
an = (1+1/n)n
= nC0・1n+nC1・1n-1(1/n)1+…+nCn(1/n)n
= 1+n/n+nC2・1n-2(1/n)2+…+nCn(1/n)n
ここで、2 以上 n 以下の自然数 k について、
nCk・1n-k(1/n)k
= {n(n-1)・・・(n-k+1)}/k!×1/(nk)
の部分を正確に計算します。
(n-1)・・・(n-k+1) は、(k-1) 個の項の積です。
1/(nk) = 1/n×(1/n)k-1 なので、
n と 1/n で約分して、
残りの 1/n を分母にもってきます。
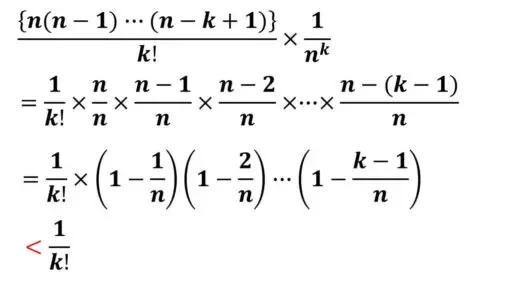
nCk・1n-k(1/n)k< 1/k! ということが分かりました。
よって、
an = (1+1/n)n
< 1+1+1/2!+1/3!+…+1/n!
この不等式は、数列 {an} が上に限界があることに使います。
後で無限級数の収束を使って、詳しく証明します。
ここまでの内容を整理します。
a1 = 1+1 です。
n ≧ 2 のときに、式の変形を行いました。そして、k は 2 以上 n 以下の自然数を動きました。
a2 = 1+1+1/2!(1-1/2),
a3 = 1+1+1/2!(1-1/3)+1/3!(1-1/3)(1-2/3),
・・・
感覚的に単調増加な雰囲気ですが、文字を使って、大小関係を示しておきます。
よって、2 以上の自然数 h について、
ah =
2+1/2!(1-1/h)+…
…+1/h!(1-1/h)…{1-(h-1)/h},
ah+1 =
2+1/2!{1-1/(h+1)}+…
+1/h!{1-1/(h+1)}…{1-(h-1)/(h+1)}
+1/(h+1)!{1-1/(h+1)}…{1-h/(h+1)}
そのため、2 以上 h 以下の自然数 t について、
1/t!{1-1/(t+1)}…{1-(t-1)/(t+1)}
-1/t!(1-1/t)…{1-(t-1)/t}
という差を計算すると、どの括弧の中も、引かれる方の値の方が大きくなっているため、差の値は正の数です。
{1-i/(t+1)}-(1-i/t)
= i/t-i/(t+1) > 0
(ただし、i = 1, … , t-1)
分子が同じ自然数だと、分母の自然数が大きい方が小さい値ですので、通分しなくても大小関係が分かりました。
さらに、ah+1 には、
1/(h+1)!{1-1/(h+1)}…{1-h/(h+1)} という正の項が、まだ残っています。
よって、ah+1-ah > 0 です。
これで、
a1 < a2 < … < an < an+1 < … となっていることが示せました。
数列 {an} が単調増加であることが示せたので、上には限界があることを示します。
そのために、一つ補題を証明します。
自然数の大小関係の補題
【補題】
k を 3 以上の自然数とすると、
k! > 2k-1 となる。
<証明>
k = 3 のとき、
3! = 3×2! = 6,
23-1 = 2×22-1 = 4
よって、3! > 23-1 となり、k = 3 のときに成立しています。
k = h のときに h! > 2h-1 が成立していると仮定します。ただし、この h は 3 以上の自然数とします。
h! > 2h-1 の両辺に (h+1) を掛けると、
(h+1)! = (h+1)h! > (h+1)2h-1
さらに、
h+1)2h-1 ≧ 2・2h-1 = 2h
すなわち、
(h+1)! > 2h となり、
k = h+1 のときにも成立しています。
よって、数学的帰納法より、
どの 3 以上の自然数 k についても、
k! > 2k-1 です。【証明完了】
k = 1, k = 2 のときは、直接計算から、
k! = 2k-1 となっていることが分かります。
では、この補題を用いて、上に限界があることを示します。
ネイピア数 :上に限界という上界の存在
ここまで、上に限界があるという非数学的な言い方をしてきましたが、正確な大学数学で使う用語を説明します。
実数全体の空集合ではない部分集合を S とします。
実数 r が、S のどの要素(元)s に対しても、
r ≧ s となっているときに、r を s の上界といいます。
この上界となる実数が一つでも存在するとき、S は上に有界といいます。
今、an = (1+1/n)n を一般項とする数列 {an} の各項を全て集めた集合を考えます。
{an | n は自然数} は、実数全体の空集合ではない部分集合となっています。
この上界となる実数が存在するということを示すのが、次の目標です。
つまり、数列 {an} のどの項の値についても、その値以上となっている実数の存在を示すということです。
先ほど示したように、数列 {an} は単調増加なので、n が大きくなると、順に第 n 項の値が大きくなっていきます。
しかし、この実数を越えないと断定したいわけです。
そこで、上で導いた不等式が効いてきます。
各自然数 n に対して、
an = (1+1/n)n
< 1+1+1/2!+1/3!+…+1/n!
となっていました。
1+1/2!+1/3!+…+1/n! の部分が、収束するということを示します。
無限級数が収束するかどうかという問題となりました。ここで部分和という新しい数列を考えます。
自然数nに対応する値
自然数 n に対して、
bn = 1+1/2!+1/3!+…+1/n! という関数を定義します。
この関数は自然数全体を定義域とし、各自然数 n に対して実数(有理数)を対応させています。定義域が自然数全体なので、数列です。
各自然数 n に対して、
an = 1+bn という関係です。
この数列 {bn} が収束することを示します。
bn+1-bn = 1/(n+1)! > 0 より、
数列 {bn} は単調増加です。
そのため、n が 3 以上のときを考えます。
【補題】より、k! > 2k-1 (k ≧ 3) だから、
1/k! < 1/2k-1 (k ≧ 3) となっています。
また、1/2! = 1/2 なので、
bn = 1+1/2!+1/3!+…+1/n!
< 1+1/2+1/22+1/23+…+1/2n-1
この右辺は、初項 1、公比 1/2、項数 n の等比数列の和です。
そのため、
1+1/2+1/22+1/23+…+1/2n-1
= {1-(1/2)n}/{1-(1/2)}
= {1-(1/2)n}÷(1/2)
= 2-2(1/2)n
よって、各自然数 n に対して、
bn < 2-2(1/2)n となっています。
n → ∞ としたとき、(1/2)n は 0 に収束するため、
2-2(1/2)n は 2 に収束します。
したがって、各自然数 n に対して、
an = 1+bn ≦ 1+2 = 3
これで、数列 {an} について、どの項の値も 3 以下ということが示せました。
つまり、{an | n は自然数} という実数全体の空集合ではない部分集合は、上に有界です。
ここまでで、示せたことをまとめます。
<まとめ>
■ an = (1+1/n)n を一般項とする数列 {an} が単調増加
■ 数列 {an} は上に有界
「a1 < a2 < … < an < an+1 < …」
ならば、
「a1 ≦ a2 ≦ … ≦ an ≦ an+1 ≦ …」ということになります。
「≦」になっているとき、単調非減少といいます。
そのため、数列 {an} が単調非減少ということになります。
実は、これで、数列 {an} が収束したことを示せたことになります。
その理由は、大学の数学の内容になるのですが、その内容を説明します。
ネイピア数 :実数についての公理
【重要な事実】
上に有界な単調非減少な数列は収束する。
有界な単調数列より
このことから、an = (1+1/n)n を一般項とする数列 {an} が収束することになります。
この収束値を e とし、e のことをネイピア数と定義します。
実は、「上に有界な単調非減少が収束する」ということは、実数の連続性の公理と同値になります。
公理というくらいで、無条件に正しいこととして認めて使うものですが、同値な条件がいくつかあります。
岩井の数学ブログという数学のサイトでは、ワイエルストラウスの条件を実数の連続性の公理として、それを公理として認めるならば、「上に有界な単調非減少が収束する」という内容が導けるということをリンク先の記事で解説しています。
実は、逆に「上に有界な単調非減少が収束する」ということを実数の連続性の公理とすると、ワイエルストラウスの内容などが導かれます。
この内容は、大学の数学の内容で、同値であることを確かめるのは、大変ですが、事実として触れておきます。
an = (1+1/n)n を一般項とする数列 {an} の収束値をネイピア数 e として定義をしているということ自体は、高校の数学3の内容となります。
実数の連続性の公理と、同値な条件たちに振り回されることなく、e を底とする自然対数などの数学3の学習を着実に押さえることが、まずは大切かと思います。
関連する記事として、常用対数という底 10 の対数関数についての数2の内容を投稿しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。