シグマ記号 – 意味 | 項の和を計算する仕組み【数B】

2022年1月5日

" シグマ記号 “が表している内容を正確に理解しておくと、何を計算しているのか分かってきます。

公式を暗記して数字を当てはめていくことは、学習し始めたときに慣れるための練習になります。

しかし、それには限界があるので、やはり、記号の意味を理解し、計算の仕組みを理解することが大切になります。

この記事では、添え字が動く範囲と、その添え字の値に対応する項を把握する定義を把握することを中心に解説します。

シグマ記号 – 意味 :定義を把握すること

【記号の意味】

Σ_k=13 a_k = a₁+a₂+a₃,
Σ_i=79 b_i = b₇+b₈+b₉

シグマ記号の定義を把握するときに、添え字（変数）が動く範囲と添え字（変数）の値に対応する項を認識することが基本になります。
　
図の上のシグマ記号から説明をします。

シグマ記号の下に書いている k が添え字（変数）です。
　
k = 1 という部分の 1 と、シグマ記号の上に書いている 3 が、k の動く範囲を表しています。

1 以上 3 以下の自然数を k は値としてとるということです。この変数（添え字）の動く範囲を正しく認識することが重要になります。
　
変数（添え字）が動く範囲が認識できたら、それぞれの変数の値に応じて、どういう項が定まってくるのかということを確認します。
　
k = 1 のとき、1 という自然数に対応して、a₁ という項が定まります。まさに、k に 1 を代入することで、項が対応してきます。
　
同じく、k = 2 のとき、自然数 2 に対応するのが、項 a₂ です。k = 3 については、項 a₃ が対応します。

変数（添え字）が動く範囲と、その範囲内の値に応じて定まる項が認識できたら、それらの項をすべてで加法を計算します。

この加法の計算結果が、シグマ記号がとる計算の値ということになります。

【まとめ】

・変数（添え字）の認識
・変数（添え字）の動く範囲
・それぞれの変数（添え字）に対応する項
　
→すべての項で加法を計算すると、それがシグマ計算のとる値

では、この手順（数学的アルゴリズム）に基づいて、図の下に書いているシグマ記号をよく見てみます。

シグマ記号の練習

Σ_i=19 b_i（i は 7 から 9 まで動く）

先ほどの図の Σ の下の i = 7 と Σ の上の 9 が意味する内容について、説明します。

∑_i=79 b_i = b₇ + b₈ + b₉ です。

まず、変数（添え字）を認識します。

シグマ記号の下に書いている文字が i なので、i が変数（添え字）です。
　
i が動く範囲は、7, 8, 9 という連続した自然数になります。シグマ記号の下の自然数から上の自然数まで連続して動きます。
　
i がとる値に応じて、どの項が対応するのかを確認します。
　
7 に対して b₇、8 に対して b₈、9 に対してb₉ が対応しています。対応する項を認識できました。そうすると、後は、それらの項すべてで加法を計算するということになります。
　
特に、「変数（添え字）の値に対応する項」という部分が大切になります。ここを押さえておかくと、様々な状況を分析できるようになってきます。

高校生のときの私が、シグマ記号を学習し始めたときに、とりあえずテスト範囲の練習問題のやり方を覚えました。

そうすると、大学受験の模試で、全く見たことがないタイプのシグマ計算が出てきて失敗しました。
　
こうならないように、基本となる定義を着実に押さえて、状況に適したことを考えることが大切かと思います。

シグマ記号 :定義に基づいた判断

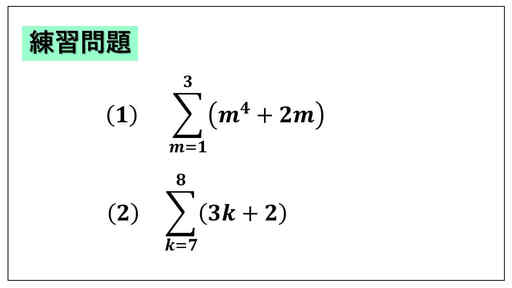
(1) から解説をしていきます。変数は m で、動く範囲は、1 以上 3 以下の自然数です。

これら変数のとる値に対応する項を確認します。
　
m = 1 に対応する項は 、(1⁴ +2 × 1) です。
　
この項は具体的に計算できるので、
1⁴ + 2 × 1 = 1 + 2 = 3 と計算しておきます。
※ 問題によっては、この段階で計算をしないで、すべての項の和を考えた方が良いときもあります。
　
m = 2 に対応する項は、
(2⁴ +2 × 2) = 20 です。
　
m = 3 に対応する項は、
(3⁴ +2 × 3) = 87 です。

三つの各自然数に対応して、項が三つ確認できました。シグマ記号の定義から、これら三つの項すべてで加法を計算します。
　
3 + 20 + 87 = 110 が (1) の計算結果となります。
　
次に (2) を解説します。変数は k で、動く範囲は 7 以上 8 以下の自然数です。つまり、変数 k がとる値は、7 と 8 です。
　
k = 7 に対応する項は、
(3 × 7 + 2) = 23 です。
　
また、k = 8 に対応する項は、
(3 × 8 + 2) = 26 です。
　
すべての項で加法を計算すると、
23 + 26 = 49 となります。

が求める計算結果となります。
　
ちなみに、三乗和の公式というブログに三乗の展開公式に関連する内容を書いています。展開公式や因数分解公式を合わせてシグマ計算を行うことが、しばしばあります。
　
日頃からの計算のトレーニングは効いてくるかと思いますので、基礎となる計算と合わせてシグマ計算を学習すると、良い相乗効果があるかと思います。
　
ここから、シグマ記号の代表的な公式を解説します。

シグマ記号 :よく使う計算公式

まずは、シグマ記号の下に書かれている変数とは異なる定数についてのシグマ計算の定義です。

公式として、押さえておく必要がある内容になります。
　
その後で、シグマ記号が分配される内容について説明をします。シグマ計算を進めていく上で、土台になる操作になります。

変数と独立な定数の和

【定数の和】

■ Σ_k=1n a = na （ただし、a は定数）

【例】
Σ_j=14 3 = 3+3+3+3
= 4 × 3 = 12

上の式は、高校数学で学習するシグマ計算の公式になっています。

変数と独立した定数の和についての内容です。
　
具体的な下のシグマ計算の例で、この内容を説明します。

変数が j です。

しかし、シグマ計算をするときの項になるであろう部分に、j が一つもなく、定数 3 が書かれています。
　
このときの定義は、j = 1 に対応する項が 3 です。j = 2 に対応する項も 3 です。
　
くどいですが、j = 3 に対応する項は 3 で、j = 4 に対応する項も 3 です。

したがって、変数 j のとる 4 つの値に対応するそれぞれの項は すべて 3 ということです。

このため、3 を 4 個で加法を計算するということになります。

4 × 3 = 12 です。同じ 3 を 4 個足すということは、3 を 4 倍するということになります。

上の公式だと、k のとる 1 つの値に対応する項は a ということになります。どの k の値にも、対応する項は a です。
　
k は 1 以上 n 以下の自然数を動くので、n 個の項が現れます。そのため、加法を計算するときの項は、a が n 個あるということになります。
　
a を n 個足すということは、a を n 倍するので、na となります。

シグマ計算の公式

Σ_kn a_k + Σ_kn b_k = Σ_kn (a_k + b_k)
k は 1 から n まで動く

自然数 k が 1 から n まで動いたときに、左辺の加法について、結合法則と交換法則を使うことで、右辺に書き換えることで、証明ができます。
　
左辺は、
(a₁+a₂+ … +a_n) + (b₁+b₂+ … +b_n)

なので、右辺と等しくなります。
　
(a₁+b₁)+(a₂+b₂)+ … +(a_n+b_n) が右辺なので、左辺と一致します。
　
次の公式は、分配法則から導かれる公式です。

t を定数とし、自然数 k を 1 から n まで動かすとき、
Σ_kn ta_k = t × Σ_kn a_k

左辺を書き出すと、どの項にも定数 t が掛けられていることが分かります。

そのため、t でくくり出すと、右辺に一致するという証明になります。
　
左辺は、ta₁ + ta₂ + … + ta_n

t でくくり出すと、
t(a₁+a₂+ … +a_n) = t × Σ_kn a_k

確かに右辺と一致しました。
　
次の公式は、等差数列の和の公式をシグマ記号を使って表したものと、等比数列の和の公式をシグマ記号を使って表したものです。
※ どちらも、k は 1 から n までの自然数を動くとします。

【等差数列の和】

Σ_kn k = 1+2+…+n
= n(n + 1) / 2

【等比数列の和】

Σ_kn ar^k-1 = a+ar+…+ar^n-1
= a(rⁿ － 1) / (r － 1)

どちらも、シグマ計算に現れる各項をすべて書き出してみます。

そうすると、上のシグマ計算は、左辺が初項 1 交差 1 の等差数列の和ということになります。
　
そのため、項数 × (初項 + 末項) ÷ 2 という等差数列の公式から、右辺と等しいということになります。
　
下のシグマ計算では、初項 a で公比 r の等比数列の和となっています。
　
等比数列の和の公式から、右辺と等しいことになります。

なお、等比数列の和の公式ですが、右辺の分子の r の指数は項数となります。

この項数は、シグマ計算で足し合わせた項の数と同じになっています。
　
あと、この等比数列の和の公式は、r が 1 よりも小さいときに、分子と分母に －1 を掛けたものを使うと計算が楽になります。
　
シグマ記号の基本となる定義と性質を押さえることで、数学の学習の土台となるかと思います。
　
このシグマを使った内容として、
期待値という確率変数のブログ記事を書いています。
　
統計分野は、よくシグマ計算を使って式を書き換えるときがあるので、良い応用例になるかと思います。
　
最後に二項定理と多項定理について述べておきます。これも、シグマ計算の仕組みに関わる内容となります。
　
難しい大学の記述問題の練習と思って証明をご覧頂ければと思います。

シグマ記号 :二項定理

【二項定理】
自然数 n について、(a + b)ⁿ を展開したときにパスカルの三角形の n 行目の並びで各項の係数が現れて、次のようになる。

すなわち、
_nC₀aⁿb⁰ + … + _nC_ra^n-rb^r + … + _nC_na⁰bⁿ
(= Σ_rnC_ra^n-rb^r)

＜証明＞

n = 1 のとき、(a + b)¹ = a + b で、
₁C₀a^1-0b⁰ + ₁C₁a^1-1b¹ = a + b なので、成立しています。
　
よって、以下で、2 以上の自然数 n に対して、定理が成立しているとして、n + 1 についても成立することを示します。

まず、指数の意味から、
(a + b)ⁿ⁺¹ = (a + b)(a + b)ⁿ
= a(a + b)ⁿ + b(a + b)ⁿ
… (1)

この (a + b)ⁿ に帰納法の仮定を使います。

_nC₀aⁿb⁰ + … + _nC_ra^n-rb^r + … + _nC_na⁰bⁿ
が (a + b)ⁿ なので、
a(a + b)ⁿ =
_nC₀aⁿ⁺¹b⁰ + … + _nC_ra^n+1-rb^r + … + _nC_na¹bⁿ
… (2)

また、
b(a + b)ⁿ =
_nC₀aⁿb¹ + … + _nC_ra^n-rb^r+1 + … + _nC_na⁰bⁿ⁺¹
… (3)

ここで、1 ≦ k ≦ n について、
(2) の b^k については _nC_ka^n+1-kb^k で、
(3) の b^k については _nC_k-1a^n-k+1b^k となっています。
※ (3) は、r に k – 1 を代入しました。
　
よって、
_nC_ka^n+1-kb^k + _nC_k-1a^n-k+1b^k
= (_nC_k + _nC_k-1)a^n+1-kb^k
= (_n+1-1C_k-1 + _n+1-1C_k)a^n+1-kb^k
= _n+1C_k a^n+1-kb^k

この変形は、(n + 1) 個から 1 個を選ぶということは、「特定の 1 個を選ぶ場合と特定の 1 個を選ばない場合」があるからです。
※ 組合せの公式というブログ記事で、この内容を解説しています。
　
aⁿ⁺¹b⁰ について
_nC₀ aⁿ⁺¹b⁰ = _n+1C₀ aⁿ⁺¹b⁰

a⁰b^k+1 について
_nC_n a⁰bⁿ⁺¹ = _n+1C_n+1 a⁰bⁿ⁺¹

以上より、
(1) = (2) + (3) だから、
(a + b)ⁿ⁺¹ は、
_n+1C₀ aⁿ⁺¹b⁰+ …+_n+1C_k a^n+1-kb^k + …+ _n+1C_n+1 a⁰bⁿ⁺¹ となっています。【証明完了】

※ 二項定理を用いたシグマ計算の練習として、
4乗のシグマというブログ記事を投稿しています。
　
次に、二項定理を用いて、多項定理も証明しておきます。

多項定理の証明

【多項定理】
自然数 n が 0 以上の整数 p, q, r を用いて、
p + q + r = n と表されているとき、
(x + y + z)ⁿ の x^py^qz^r の係数は
n! ÷ (p!q!r!) = n!/p!q!r! となる。

＜証明＞

(x+y+z)ⁿ = {(x+y)+z}ⁿ なので、二項展開をするときの一般項は、
_nC_r(x+y)^n-rz^r です。

この r は、0 から n まで動きます。
　
さらに、p + q + r = n なので、
n – r = p + q に書き換えると、
_nC_r(x+y)^p+qz^r です。

よって、
(x+y+z)ⁿ は、
_nC₀(x+p)^p+qz⁰+…+_nC_n(x+p)^p+qzⁿ
= Σ_rnC_r(Σ_kp+qC_kx^p+q-ky^k)z^r
= Σ_rΣ_knC_r・_p+qC_kx^p+q-ky^kz^r

※ r は 0 から n まで動き、k は 0 から p + q まで動きます。
　
ここで、x^py^qz^r の係数を求めてみます。
上の最後の式で、k = q のときの係数となります。
　
k = q のとき、p + q － k = p となります。
　
したがって、x^py^qz^r の係数は、
_nC_r × _p+qC_q です。

この値を計算すると、
n!/r!(n – r)!
× (p+q)!/(p+q-q)!q!

よって、
n!/r!(p+q)! × (p+q)!/p!q!

分数を約分すると、
n! / p!q!r! です。

これが、x^py^qz^r の係数です。【証明完了】

二項定理や多項定理の証明するときの計算は、シグマ計算の考え方に基づいて実際に実行すると、大学受験の記述証明のレベルになります。

また、シグマの計算から、階差数列ともとの数列の一般項を結び付けることもできます。

高校一年で学習したデータの分析ですが、シグマ記号を学習すると、分散などと合わせてシグマ記号が使われることもあるので注意です。

それでは、これで今回のブログ記事を終了します。

読んで頂き、ありがとうございました。