1/6公式 | そのマイナスは、どういうことなのか【接点と方程式の重解も解説】
1/6公式 , その式にはマイナスがついています。この疑問を解決することで、自信をもって文字が使われている状態でも議論を進めていけるようになります。
高校生だった頃の私は、はじめのうちは「公式を使ったときの数字さえ、答えと合っていれば良いや」と軽く考えていました。
しかし、文字が使われている状態で、証明問題などを議論しているときに、符号がプラスなのかマイナスなのかが？になってしまいました。
そのため、深く議論を進められなくなったり、解説が理解できなくなったりしました。
そのようなことを無くせるように、マイナスの部分を理解できるように、公式の証明のプロセスを説明します。
また、この手の内容では、多項式についての一般論も使うので、合わせて学習の理解を深めるチャンスになります。
それでは、基礎となる内容から議論を詰めていきます。
1/6公式 :係数が1のときの証明
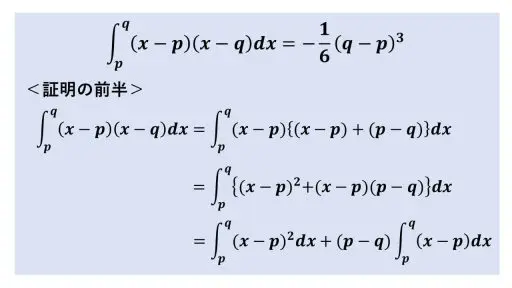
x2 の係数が 1 のときの証明の前半です。なお、p ≦ x ≦ q が積分区間で、p と q は定数です。
積分変数は、x です。そのため、定積分を計算するときには、p と q は定数なので、乗法をするときに、積分⊂（インテグラル）の外に出ます。
この証明の前半では、1/6公式の左辺を三番目の式へと変形しました。後は、三番目の式を計算すると、示したい等式の右辺となります。マイナスが絡んでくるので、その部分を確認します。
地味ですが、途中で使った多項式の変形は、しばしば使う変形を使いました。
x － q = (x － p) + (p － q) で、(x － q) の部分を敢えて書き換えることで、定数倍を積分記号の外へ出すことができました。
それでは、後半の証明です。
後半の証明
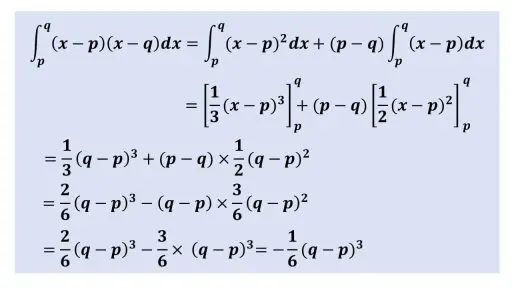
これで、x2 の係数が 1 のときの証明が完了しました。確かにマイナスがついています。
今、証明したものは、等式が成立するという内容の命題でした。
数学では、既に成立している命題を利用することができます。
既に成立している命題を利用
次に目指すのは、x2 の係数が a のときです。文字を使っていますが、この a は定数です。
これが、x2 の係数が a のときの等式です。ここで、ふと疑問に思われる方が出てくるかもしれません。定積分を使って、面積を定めていました。
ところが、この公式で、a が正の実数のときに、二次関数を定積分した値が負の実数となります。
そうなんです、ただ関数を定積分で計算したというときには、積分の値が負の実数となることもあるんです。
高校の数学で、面積を定積分を使って求めるときには、設定がありました。
積分区間において片方の関数のグラフが、もう一方のグラフの上側にあるという設定です。
そして、上側のグラフを下側のグラフで引いてから積分区間において定積分を計算しています。
y = g(x) と y = h(x) について、
p ≦ x ≦ q のときに、g(x) ≦ h(x) となっているときに曲線や直線で囲まれた部分の面積を定積分を使って定めていました。
関数 {h(x) － g(x)} を p ≦ x ≦ q において定積分すると、その値は 0 以上になっていて、面積だから 0 以上ということで納得ができました。
※ 大学数学風に言いうと、被積分関数が積分区間 p ≦ x ≦ q においてとる値が必ず 0 以上であれば、リーマン積分を計算した値は 0 以上ということです。
このような設定を考えずに、単に二次関数を定積分するというときには、積分値が負の実数となることが起こり得ます。
論より証拠というわけで、例で確認してみます。
面積のことは考えずに、定積分の定義に基づいて積分計算をした値に注目します。
定積分した値が、負の実数となる例
f(x) = 3x2－15x+18 を、
積分区間 2 ≦ x ≦ 3 において定積分したときの値は、負の実数となります。
f(x) = 3(x2 － 5x + 6) = 3(x － 2)(x － 3) と因数分解できます。
先ほどの上端 q が 3 で、下端 p が 2 となっています。そして、a が 3 です。
(3 － 1)3 は正の実数ですから、前の符号－のために、値が負の実数となることが分かります。
公式を使わずに、f(x) を計算してみます。確かに、積分値が負の実数となります。
この計算が、公式に当てはめると一瞬ですが、敢えて計算をしてみました。ただ単に定積分をしただけでは、積分値が負となることもあるという例です。
ですので、公式や定理を使うときには、どういう設定、条件の下で使えるものなのかということを意識する必要があります。
高校の定期考査などであまり扱われない部分を取り挙げてみました。というのも、大学の数学を学習するときには、あらゆる状況を考えるからです。
そうしたことも意識して、どのような可能性があるのかと考えることも、時として良い練習となるかと思います。
ちなみに、テストで 1/6公式 を使う場面として、上端・下端にルートや分数が絡んでくるときが考えられます。
公式を使わないと、途中で計算ができなくなってしまうことになるかもしれません。
しかし、上で証明した内容で、うまくキャンセルが起きるようにして積分値に辿り着けるように工夫をしているので、公式を使うとスムーズに値が求まります。
複雑なルートが出てくるものを試しに計算してみます。1/6公式が力を発揮してくれます。この公式を使わないで計算するのは、苦しいものがあるかと思う計算です。
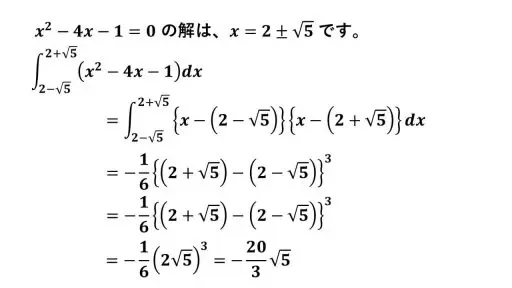
さすがに三乗の展開公式ばかりを使いたくないので、公式を利用しました。
はじめに証明したときに、工夫した変形をしておいただけのことがあって、キャンセレーションが起きて、スムーズに計算ができます。
上端・下端にルートや分数が使われている二次関数の定積分が出てきたら、1/6公式を使えるかどうかを確認してみると良いかと思います。
「二次方程式の解で、小さい値が下端、大きい値が上端」にきていたら、1/6公式を使えます。
ただ、一致していないと、証明のときのアルゴリズムの通りにならないので、使えることを確認してから使うということを注意しておくと良いかと思います。
関連する内容として、三次関数と直線の接点と方程式の重解について、以下で解説をしています。
そのときに、一部で、数学IIIで学習する積の微分の公式を使います。
【積の微分公式】
f(x)s(x) を x で微分すると
積の微分公式より
f'(x)s(x)+f(x)s'(x) となる。
数学IIIでよく使う公式ですが、これを用います。
1/6公式 :接点と重解
【定理】
直線 y = ax + b と三次関数 y = f(x) が、
点 A(t, f(t)) において接しているとする。
このとき、x についての三次方程式
f(x) － (ax + b) = 0 は x = t を重解にもつ。
＜証明＞
点 A(t, f(t)) は接点なので、直線と三次関数のグラフのどちらの上にもあります。
このため、f(t) = at + b
これは、直線の式に x = t を代入してできる式です。x = t に対応する値が y = f(t) という関数の一対一対応の定義の通りです。
右辺を左辺に移項すると、
f(t) － (at + b) = 0 … ★
この★は、
x についての方程式 f(x) － (ax + b) = 0 が、
x = t を解にもつということを示しています。
そのため、数学IIで学習する因数定理を使うと、多項式 f(x) － (ax + b) が (x － t) で割り切れるということになります。
因数定理より、
f(x) － (ax + b) = (x － t)g(x) … ☆
このように、二次の多項式 g(x) を用いて表せます。
x = t が重解なので、
f(x) － (ax + b) が (x － t)2 で割り切れることを示す必要があります。
そのために、微分を使って等式を導きます。
t は問題文の設定で、はじめから与えられている定数なので、x が変数です。
このことに注意して、両辺を x で微分します。右辺を微分するときに、数学IIIの「積の微分の公式」を使います。
つまり、
f'(x) － (ax + b)’ = f'(x) － a
= (x－t)’ × g(x)+(x－t) × g'(x)
= g(x) + (x － t)g'(x)
すべて等しいので、特に、
f'(x) － a = g(x) + (x － t)g'(x) … (1)
等式 (1) の左辺に注目します。
点 A(t, f(t)) において直線 y = ax + b が三次関数 y = f(x) に接していたので、x = t における接線の傾きは 直線の傾き a に等しいということになります。
※この直線 y = ax + b が x = t における接線です。
よって、接線の傾き f'(t) = a となっています。
a を左辺に移項すると、f'(t) － a = 0
これは、(1) に x = t を代入すると、左辺の値が 0 となるということを示しています。
そのため、右辺の多項式に x = t を代入したときの値が 0 ということになります。
すなわち、
g(t) + (t － t)g'(t) = 0 … (2)
(2) について、
t － t = 0 より、g(t) = 0
これは、二次方程式 g(x) = 0 が x = t を解にもつということを示しています。
そうすると、再び因数定理を使うことができます。
g(x) の次数は 2 なので、
g(x) = (x － t)h(x) … (3)
と 1 次式 h(x) を用いて g(x) を表すことができます。
(3) を☆に代入すると、
f(x) － (ax + b) = (x － t)g(x)
= (x － t)(x － t)h(x)
= (x － t)2h(x)
これは、x = t が、
f(x) － (ax + b) = 0 の重解であることを示しています。【証明完了】
証明で使った因数定理は基本的なので、以下にまとめておきます。
因数定理
x についての n 次方程式 f(x) = 0 が x = t を解にもつとき、多項式 f(x) は (x － t) で割り切ることができる。
割ったときの商を g(x) とすると、
f(x) = (x － t)g(x)
ただし、g(x) の次数は f(x) の次数よりも 1 だけ小さい。
この因数定理は、多項式を書き換えるときに、しばしば使われます。
関数のグラフから、方程式の解に注目して変形します。
大学受験で頻出の内容になるので、押さえておくと良いかと思います。
増減表という記事の【練習問題２】で、今回の記事で述べた1/6公式を使っています。
【関連する記事】
これで今回のタロウ岩井のブログ記事を終了します。
読んで頂き、ありがとうございました。