増減表 – 増加関数 – 減少関数 | 一次導関数の符号から【3次関数の例も】

2023年1月17日

" 増減表 “を作るときに、一次導関数 f'(x) の符号を調べます。

どの区間で増加関数となっていて、どの区間で減少関数となっているのかを押さえることが大切になります。

数学IIから微分して、" 3次関数 “の増減表を作成する流れを学習し、その背景となる理論は数学IIIで学習します。

平均値の定理の不等式の厳密証明を抜きにすると、文理共通の内容です。

平均値の定理を認め、増加もしくは減少区間を把握できる根拠を解説しています。

平均値の定理の厳密証明は他のブログ記事で解説することとして、結果だけを使うことにします。

定理の証明が数学IIIの内容を使うのですが、認めてしまうと数学IIの内容で増減表の内容を扱うことができます。

増減表 – 増加関数 – 減少関数

【平均値の定理】
関数 f が閉区間 [a, b] で連続、かつ 開区間 (a, b) で微分可能とする。

このとき、ある実数 c が存在して、
a < c < b かつ
f(b) – f(a) = f'(c)(b – a) を満たす。

ロルの定理より

以前に書いたブログ記事で、理系の方に向けて厳密証明の部分を解説しています。

今回の記事では、この内容を使う応用として、増減表について解説をします。
　
ある実数 c が存在して、
a < c < b かつ
f(b) – f(a) = f'(c)(b – a) という部分が増減表の内容になります。
　
a < c < b という範囲が増減表に記述する区間となります。

導関数の符号と増加区間

【命題1】

a と b を実数とし、開区間 (a, b) 内の任意の実数を c とする。
また、関数 f(x) は (a, b) において微分可能であるとする。

このとき、f'(c) > 0 が常に成り立つならば、
関数 f(x) は開区間 (a, b) において増加関数である。

＜証明＞
今、a < c < b より、
開区間 (a, c) において f(x) は微分可能となっています。

よって、平均値の定理を適用すると、
ある実数 d が存在し、
a < d < c かつ
f(c) – f(a) = f'(d)(c – a)

d は (a, b) 内にも含まれているので、
仮定より、f'(d) > 0

a < c なので、c – a > 0 であり、正の実数どおしで掛け算を計算した値は正となります。

そのため、
f(c) – f(a) = f'(d)(c – a) > 0

つまり、f(a) < f(c)

任意に取った開区間 (a, b) 内の c に対して、
c < e < b である任意の実数 e を取ります。
　
そして、先ほどと同様の議論を繰り返すと、
f(c) < f(e) です。

これは、(a, b) 内から c < e となっている実数 c と e を任意にとると、f(c) の値よりも f(e) の値の方が大きな値となっていることを示しています。

ゆえに、関数 f(x) は (a, b) において増加関数となっていることが示せました。【証明完了】

この手の不等式を絡めた証明ですが、< を > と逆にして同様の議論を繰り返すことができるときがあります。

この不等式の双対性から、減少区間についての命題も証明できます。

減少区間となる理由

【命題2】

a と b を実数とし、開区間 (a, b) 内の任意の実数を c とする。
また、関数 f(x) は (a, b) において微分可能であるとする。

このとき、f'(c) < 0 が常に成り立つならば、
関数 f(x) は開区間 (a, b) において減少関数である。

この【命題2】は、【命題1】と導関数の符号が逆になっています。

不等号の向きを逆にして、同様の考察をすると、減少区間となっていることが証明できます。
　
f'(d)(c – a) が先ほど正の実数どおしの積だから、値が正となっていたところが、負の数と正の数の積だから値が負となります。
　
この双対的な証明は、同じ要領のものを書くだけなので省略します。
　
それでは、具体例を通して【命題1】と【命題2】の内容を説明します。抽象的な理論ですが、具体的な例を用いて考えてみると、より理解しやすいかと思います。

数学2の内容で三次関数について増減表を作成します。

増減表 – 3次関数 – 作成

f(x) = x³ – 9x² + 24x という三次関数についての増減表を作成します。
結果の表を先に述べておきます。

f'(x) = 3×2－18x+24
= 3(x－2)(x－4) より、
f'(x) = 0 は、「x = 2 または x = 4」と同値です。

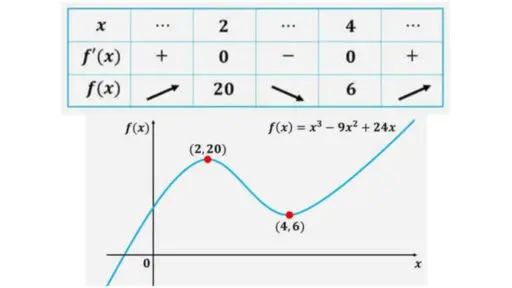
[1] x < 2 のときは、関数 f(x) は増加関数。
[2] 2 < x < 4 のとき、f(x) は減少関数。
[3] 4 < x のとき、f(x) は増加関数。

この増減表の内容に基づいて、三次関数のグラフを描くと次のようになっています。

x < 2 の範囲では、単調に増加し、
2 < x < 4 の範囲では、単調減少です。

そして、4 < x の範囲では、再び単調増加です。

グラフから x = 2 で極大値 20 をとり、x = 4 で極小値をとるということが分かります。

ただし、定義域を実数全体で考えていると、最大値と最小値は存在していません。グラフから、＋∞ と－∞ に発散しています。
※ max-min というブログ記事で、最大値と最小値について解説をしています。

最後に、平均値の定理から、この内容を不等式で確認しておきます。

b－a = f'(c)(b－a) を満たす
実数 c が、
a < c < b となる範囲に存在するという定理を基礎として議論を進めます。

三次関数 – 例

f(x) = x³ – 9x² + 24x について、不等式を平均値の定理から考察してみます。

開区間 (p, 2) において、単調に増加していることを確認します。

f'(x) = 3x² -18x + 24
= 3(x -2)(x – 4)

f'(x) は二次関数になっていて、x < 2 の範囲では、f'(x) の値は正となっています。

p < t < 2 である任意の実数 p と t について、
開区間 (p, t) において【命題1】より、
p < d < t である実数 t が存在して、
f(t) – f(p) = f'(d)(t – p)
※ 平均値の定理に関連する内容です。

f'(d) > 0, t – p > 0 より、
f(p) < f(t) です。

開区間 (t, 2) においても同様にして、
f(t) < f(2) となります。

よって、f(p) < f(t) < f(2)

x < 2 の範囲では、関数 f(x) は単調増加関数となっています。
このため、先ほどの三次関数のグラフの x < 2 の部分が描けました。

今度は 2 < r < s < 4 の範囲で平均値の定理を考えます。

開区間 (2, s) において、f(x) は微分可能で、
f'(x) = 3(x – 2)(x – 4) であり、
2 < x < 4 について、f'(x) < 0

開区間 (2, r) で【命題2】を適用すると、
2 < d < r である実数 d が存在して、
f(r) – f(2) = f'(d)(r – 2) < 0

※ f'(d) < 0, s – 2 > 0 より不等号ができました。

よって、f(2) > f(r)

開区間 (r, s) において【命題2】を適用すると、
r < e < s である実数 e が存在して、
f(s) – f(r) = f'(e)(r – s) > 0

つまり、f(r) > f(s)

ゆえに、2 < r < s について、
f(2) > f(r) > f(s) となっています。

開区間 (s, 4) についても、
同じ要領で考えると、
f(s) > f(4) となります。

これで、区間 2 < x < 4 において、関数 f(x) が単調減少関数だということが分かりました。

4 < x の範囲については、
f'(x) > 0 となることから、【命題1】から、再び増加関数になっていることが示せます。

自分で文字を設定

理系の方だと、大学受験などで、平均値の定理を使って、不等式を証明することも必要になります。

そのときに、自分で文字を設定するとうまく説明ができるときがあります。

4 < x において f'(x) > 0 ということを利用して、単調増加であることを示すときには、
4 < a < b である任意の実数 a と b を考えます。

開区間 (a, b) において、
f'(x) > 0 なので、【命題1】が適用できるようになります。

a < k < b である実数 k が存在して、
f(b) – f(a) = f'(k)(b – a) > 0

よって、f(a) < f(b)

開区間 (4, a) についても同様にして、
f(4) < f(a) です。

したがって、
4 < a < b について、
f(4) < f(a) < f(b) となっているので、
4 < x の範囲で f(x) は単調増加関数となっています。

ここからは、極大値と極小値の和に関連する三次関数の問題を解説します。

極大値と極小値の和 :準備の内容

y = f(x) を三次関数とするとき、この関数が極値をもつことの必要十分条件が分かっています。

f'(x) は二次関数なので、
f'(x) = 0 という x についての二次方程式が異なる二つの実数解をもつときに、もとの三次関数が極大値と極小値をもちます。

必要十分条件なので、f'(x) = 0 が異なる二つの実数解をもつことと、三次関数が極値をもつということを適宜、書き換えて使うことができます。

そこで、三次関数が極値をもつとき、
f'(x) = 0 の二つの解を x = a, b としたときに解と係数の関係が使えます。

a+b, ab の値を、この関係で押さえておき、基本対称式についての式の変形を行って計算を進める流れとなります。

そこで、高一の頃から計算の単元で出てきた式の書き換えを復習しておきます。

今回は、数２の微分の単元についての記事ですが、基本対称式を使った式の書き換えを利用します。

計算単元の復習

a+b = s, ab = t とします。

このとき、
a²+b² という式を次のように書き換えることができます。

a²+b² = (a+b)²－2ab
= s²－t となります。

二乗の差については、
a²－b² = (a+b)(a－b) なので、
a－b の値が決定できれば、この式から書き換えることができます。

(a－b)² = (a+b)²－4ab
= s²－4t ということから、
a－b をプラス・マイナスとルートを使った形で強引に計算するときもあります。

ただ、この方法をする前に、a－b の値が、問題文からの条件を考えるとスムーズに決定できることがあるので、二乗の差については注意をしておくと良いかと思います。

※ こちらの記事で三乗和の公式について解説をしています。

この記事では、その結果を使うことにします。

a³+b³ = (a+b)³－3ab(a+b)
= s³－3ts
= s³－3st となります。

これで三乗和の公式と結びつけて考えます。

なお、b に －b を代入すると、
a³－b³ = (a－b)³+3ab(a－b) となります。

やはり、a－b の値が決定できていれば、三乗の差についての値も決定できるということになります。

それでは、これらの高一の計算の復習内容を使って、極大値と極小値の和を求める問題を扱います。

極大値と極小値の和 :実践練習

【練習問題１】

実数 p を定数とし、
f(x) = x³+px²+px+3 という三次関数が与えられたとします。

そして、この三次関数が x = a, b (a, b は実数で a < b) において、極値をもつとします。

さらに、f(a)+f(b) = 6 とします。

このとき、定数 p の値を求めてください。

必要条件・十分条件を考慮した論理が効果を発揮します。

三次関数が極値をもつため、
f'(x) = 0 という x についての二次方程式が異なる二つの実数解をもちます。

f'(x) = 3x²+2px+p なので、
3x²+2px+p = 0 が異なる二つの実数解 a, b をもつことになります。

解と係数の関係から、
a+b = －2p/3, ab = p/3 です。

今度は、二次方程式についての書き換えを行います。

p についての範囲も押さえておきます。

最後に値を決定するときに、この範囲が決め手になるので、忘れないように注意です。

この判別式を D とすると、異なる二つの解をもつことから、D の値は 0 より大きくなっています。

2p が一次の項の係数より、
D/4 = p²－3p > 0 です。

すなわち、
p(p－3) > 0 です。

そのため、
p < 0 または p > 3 …★

この p についての範囲は最後に使います。

仮定された等式を利用

f(a)+f(b) = 6 と問題文に書かれていました。

この極大値と極小値の和について、解と係数の関係で得られた等式を利用することを考えます。

x = a, x = b を与えられた三次関数の式に代入します。

f(a) = a³+pa²+pa+3,
f(b) = b³+pb²+pb+3 です。

これらを辺々足すと、
f(a)+f(b) =
(a³+b³)+p(a²+b²)+p(a+b)+6 となります。

仮定より、f(a)+f(b) = 6 より、
(a³+b³)+p(a²+b²)+p(a+b)+6
= 6 です。

つまり、
(a³+b³)+p(a²+b²)+p(a+b) = 0 です。

これは、解と係数の関係を使うしかないじゃないかというくらい基本対称式を使った書き換えのチャンスです。

三乗和から順に書き換えます。

a+b = －2p/3, ab = p/3 という先ほど導いた等式を使います。

a³+b³ = (a+b)³－3ab(a+b)
= (－2p/3)³－3・p/3・(－2p/3),
p(a²+b²) = p{(a+b)²－2ab}
= p{(－2p/3)²－2p/3},
p(a+b) = －2p²/3 です。

ちょっと計算が大変ですが、大学受験では、これくらいの量だと計算を進めることが多いです。

三つの等式を辺々足すと、左辺の値は 0 でした。

右辺の値を p を用いて計算し、0 とイコールで結びます。

よって、
p²(2p－9) = 0 です。

p についての三次方程式ができました。

ここで、上で導いた不等式★を使います。

p < 0 または 3 < p という範囲に実数 p が含まれていました。

そのため、p ≠ 0 です。

これより、
p²(2p－9) = 0 の両辺を p² で割ることができます。

つまり、
2p－9 = 0 です。

これで、p = 9/2 と求まりました。

数２になると、この問題のように論理を使った議論の進め方が多くなります。

普段から必要条件や十分条件を意識してトレーニングをしておくと良いかと思います。

最後に極大値と極小値の差に関連した問題を述べておきます。

この問題は、【練習問題１】を解いたときのように、基本対称式を使った計算で答えを求めることができます。

ただ、同じ様な解き方になるので、違ったアプローチをしてみます。

f(x) の導関数 f'(x) について、
∫ f'(x) dx = f(x)+C （C は積分定数）となることを使います。

定積分だと、積分定数が打ち消されて消滅します。

∫_st f'(x) dx = [f(x)+C]_st
= {f(t)+C}－{f(s)+C}
= f(t)－f(s) となります。

極大値と極小値の差

【練習問題２】

実数 s, t を定数とし、
f(x) = 2x³+sx²+tx という三次関数が与えられたとします。

また、実数 a, b は a < b で、
x = a, x = b において、この三次関数がそれぞれ極大値と極小値をとるとします。

さらに、b－a = 1 となっていたとします。

このとき、f(a)－f(b) の値を求めてください。

f'(x) = 6x²+2sx+t です。

f'(x) = 0 は、三次関数 f(x) が極値をもつことから、異なる二つの実数解をもちます。

ここで、x = a, b が解なので、因数定理を使います。

6x²+2sx+t = 0 の解が、
x = a, b より、
f'(x) = 6(x－a)(x－b) です。

よって、
f(a)－f(b) = [f(x)]_ba
= ∫_ba f'(x) dx
= ∫_ba 6(x－a)(x－b) dx
= －6∫_ab (x－a)(x－b) dx

上端と下端を入れ替えて、－1 倍にしたのは、1/6公式を使うためです。

二つの実数解と二次関数とくれば、この公式を使うチャンスです。

下端の値 a と左側の (x－a) の a を、上端の値 b と右側の (x－b) の b を揃えておくと、機械的に定積分の計算規則から値が従うという公式になります。

したがって、
f(a)－f(b) =
－6∫_ab (x－a)(x－b) dx
= －6×(－1/6)×(b－a)³ となります。

仮定より、b－a = 1 だから、
f(a)－f(b) = －6×(－1/6)×1³
= 1 です。

これで極大値と極小値の差が 1 と分かりました。

マーク式の問題などで短時間で問題を解くときに、1/6公式を使った素早い計算が役立つこともあるかと思います。

【他の数２の記事】

・1の3乗根オメガ
・3変数の対称式

それでは、これで今回のブログ記事を終了します。

読んで頂き、ありがとうございました。