等速円運動 | 角速度を微分の数学で理解する【高校数学III】
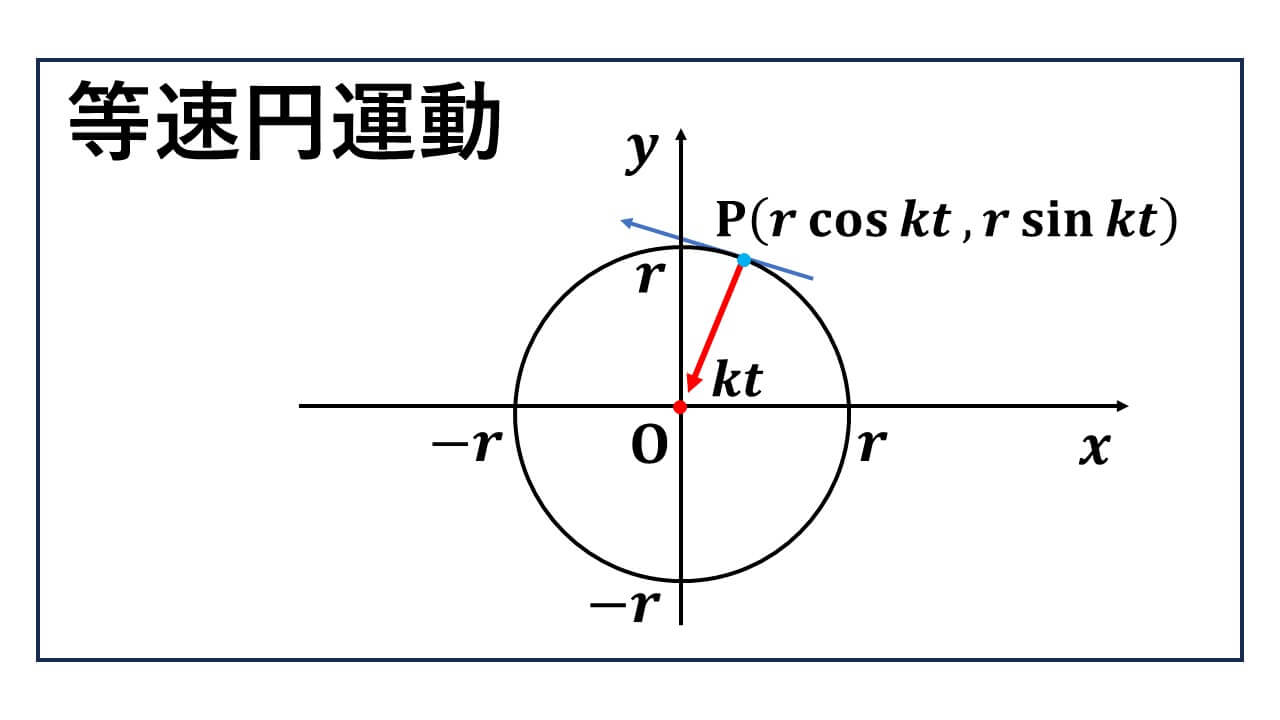
" 等速円運動 “は、数3の微分の単元で扱われます。
数学の用語を使って述べると、ベクトル値関数についての速度ベクトルの議論となります。
しかし、時間経過にともなって、角の大きさが変化するということは、理科などで既に知っている身近な内容です。
この記事では、その身近な現象を数学の関数や微分を通じて表現するということについて、基礎的な内容を解説しています。
t 時間が経過したときに、t に対して座標平面上を動く点 P の座標を対応させるという関数についての微分の内容となります。
等速円運動 :土台となる関数の内容
ベクトル値関数という聞き慣れない関数を使っているので、学習をし始めるときにハードルが高く感じるかもしれません。
しかし、用語の内容に慣れてしまえば、いたって自然な内容になっています。
xy-座標平面において、(0, 0) という原点 O を位置ベクトルの基準(始点)として、その平面上の点の位置を示す座標を考えます。
例えば、点 P が (3, 2) という位置にあるとき、原点を始点としてベクトルで表すことにします。
すると、(3. 2) はベクトルOP の成分表示となります。
座標平面のどの点も、この位置ベクトルで表すことにしておきます。
そうすると、t 時間経過したときに、実数 t に対して、点 P がいる位置を表す位置ベクトルを対応させることで、ベクトルを値として取る関数が得られます。
これがベクトル値関数です。
より正確に、t 時間が経過したときの点 P の x 座標を f(t), y 座標を g(t) と置きます。
そして、
v(t) = (f(t), g(t)) と置きます。
これが、t の定義域を 0 以上の実数全体とし、値域が平面ベクトルであるベクトル値関数です。
t = 2 のときに、
点 P が (5, 3) の位置だと、
f(2) = 5, g(2) = 3 より、
v(2) = (5, 3) ということです。
v(2) = (5, 3) は、
t = 2 のときに、
点 P の位置が (5, 3) ということを示しています。
等速円運動では、時間経過にともなって、角の大きさが規則的に変化します。
この角速度という内容に関連させ、点 P が動く速さを微分で求めます。
等速円運動というくらいで、速さは一定となります。
使う数III の理論から述べ、点 P の速度ベクトルへと議論を進めます。
微分単元の内容
【速度の理論】
v(t) = (f(t), g(t)) について、
v'(t) = (f'(t), g'(t)) が速度ベクトル。v"(t) = (f"(t), g"(t)) が加速度ベクトル。
ブログ加速度ベクトルより
時間 t が経過したときに、点 P の位置を表すベクトル値関数 v(t) を 1 回 t で微分すると加速度ベクトルです。
さらに、もう一度 t で微分をすると加速度ベクトルです。
それぞれ、速度ベクトルに絶対値をつけると、正負の向きを考慮から外した大きさだけの速さとなります。
これで、速度と加速度を表現するので、物理の内容が扱えるようになります。
等速円運動というくらいなので、点 P は一定の半径の円周上を移動します。
そのときに、円の中心と点 P を結んだ線が、横軸との間で、なす角を考えます。
そうすると、円周上の点なので、f(t) や g(t) として、三角関数を利用して内容を表現することができます。
等速円運動 :角速度を押さえる
r と k を正の実数とし、定数とします。
点 P は、原点中心、半径 r の円の周上を動くこととします。
点 (r, 0) から、線分 OP と x 軸のなす角が単位時間 1 あたり k だけ正の向きに(左回り)に動くとします。
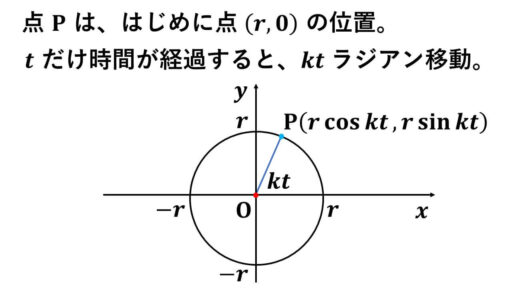
この設定から、時間が t 経過すると、OP と x 軸のなす角を計算することができます。
1 : k = t : □ という比の関係から計算できます。
□ = kt ということになります。
つまり、時間が t 経過すると、なす角は kt ラジアンということです。
角度を表す単位はラジアンにしていますが、この内容は算数や理科で学習済みの内容になります。
この時間経過にともなって、なす角が変化することと関連させつつ、ベクトル値関数の微分を用いて表すということを考えます。
経過時間が t のとき、なす角が kt であることから、点 P の位置を三角関数を使って表すことができます。
(rcos kt, rsin kt) が経過時間 t のときの点 P の位置です。
そのため、
f(t) = rcos kt,
g(t) = rsin kt とし、
v(t) = (f(t), g(t)) と定めます。
これで、時間が t 経過したときの点 P の位置を表すベクトル値関数が設定できました。
このベクトル値関数を t で微分をすると速度ベクトルとなります。
速度ベクトルに絶対値をつけると速さです。
※ 角速度 kt とは異なる値になります。
この速さが t に依存しない定数になります。
これが位置の微分
v(t) = (f(t), g(t)) で、
f(t) = rcos kt, g(t) = rsin kt となっています。
t で微分をした値を求めます。
f'(t) = -rksin kt,
g'(t) = rkcos kt です。
※ 合成関数の微分の公式を使いました。
よって、
v'(t) = (-rksin kt, rkcos kt) が速度ベクトルです。
速度ベクトルも、x 成分と y 成分を実数とする平面ベクトルとなっています。
そのため、絶対値は、x 成分の二乗と y 成分の二乗の和にルートをつけます。
そうすると速さが求まります。
ルートをつけるということは、
1/2 乗するということです。
指数計算も含めて正確に計算を進めることが大切になります。
あくまでベクトルの絶対値
|v'(t)| の値を計算します。
{(-rksin kt)2+(rkcos kt)2}1/2
= {r2k2(sin2kt+cos2kt)}1/2
= (r2k2)1/2 = rk
※ r と k は正の実数という設定なので、そのままルートを外すことができます。
すなわち、
|v'(t)| = rk です。
r, k は定数なので、rk も定数です。
速さが定数なので、点 P が左回りに円周上を動く速さが一定ということになります。
このあたりが、等速円運動という名が表す内容です。
今度は、加速度ベクトルについても考察します。
ベクトルなので、向きにも注目です。
等速円運動 :向きについても
v'(t) = (-rksin kt, rkcos kt) が速度ベクトルでした。
もう一度 t で微分をすると、加速度ベクトルになります。
v"(t) = (-rk2cos kt, -rk2sin kt) となります。
t における円上の点 P の位置の微分なので、円の接線の方向が向きとなっています。
物理でいうところの遠心力の向きです。
そのまま円の外に飛んでいきません。
その理由が加速度ベクトルの向きにあります。
計算からベクトルのスカラー倍を見てみます。
v"(t) = (-rk2cos kt, -rk2sin kt)
= -rk2(cos kt, sin kt)
= -rk2v(t) です。
v(t) は、点 O を始点とし、点 P を終点とするベクトルでした。
-rk2 は負の実数なので、
-rk2v(t) はベクトル OP と逆の向きです。
つまり、点 P から点 O の方向へ加速度の大きさの分だけ力がかかっているというわけです。
これが、遠心力で点 P が円の外に飛び出さない理由です。
点 P から円の中心 O の向きに力が加わっていて外に飛び出していくのを止めているという状況となっています。
実際、v'(t) と v"(t) で内積を計算すると、値が 0 になっています。
つまり、速度ベクトルと加速度ベクトルが垂直になっていて、加速度ベクトルの向きは円の中心に向かっているということです。
※ 内積の定義という記事で、平面ベクトルの内積について解説をしています。
今回の記事では、円周を動く点について、その速度ベクトルと加速度ベクトルを計算しました。
関連する記事について
数学3の内容を使いましたが、時間経過にともなって角の大きさが変化するということを算数や理科で学習していました。
算数や中学の数学でイメージをトレーニングしておき、数3の微分の内容を使いました。
積分については、置換積分という記事を投稿しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。