チェバの定理の逆 | 三角形の内部で交わる1点をベクトルで表す
" チェバの定理の逆 “は高校数学の平面図形の単元で学習する内容になります。
図形についての基本なだけに、ベクトルと合わせて議論を進めるということも考えられます。
この記事では、三角形の内部のただ 1 点で交わった交点を位置ベクトルを用いて表すことを解説しています。
そうすると、内分比とベクトルについてのつながりが、明確になります。
この記事では、三角形ABC の外部に点 O をとり、O を位置ベクトルの基準として、それぞれの点を位置ベクトルで表しています。
A(a) だと、点 A の位置ベクトル表示が a ということを表しています。
チェバの定理の逆 :ベクトルと図形の融合へ
【チェバの定理の逆】
三角形ABC の辺 BC, C, AB もしくはその延長上に、それぞれ点 D, E, F をとする。
そして、これら 3 点のうち、辺の延長上にある点の個数が 0 個か 2 個だとする。
このとき、
BD/DC×CE/EA×AF/FB = 1 であるならば、3 本の直線 AD, BE, CF は 1 点で交わる。
これが高校一年の平面図形の単元で学習するチェバの定理の逆という真である命題です。
真なので、結論以外のすべての内容を満たす図形の状況が出てくると、結論へとジャンプすることができます。
この記事で扱う内容としては、三角形の 3 本の辺の上に点をそれぞれ 3 個とり、チェバの定理の逆の仮定の内容を満足している状況で、さらに細かく議論を詰めます。
位置ベクトルを用いることで、ベクトルの分点公式が使えるので、内分比を正確に議論することができます。
平面図形の内容の定理とベクトルの公式を合わせることで、状況を説明する良い表現力が養われるかと思います。
仮定を満たす状況
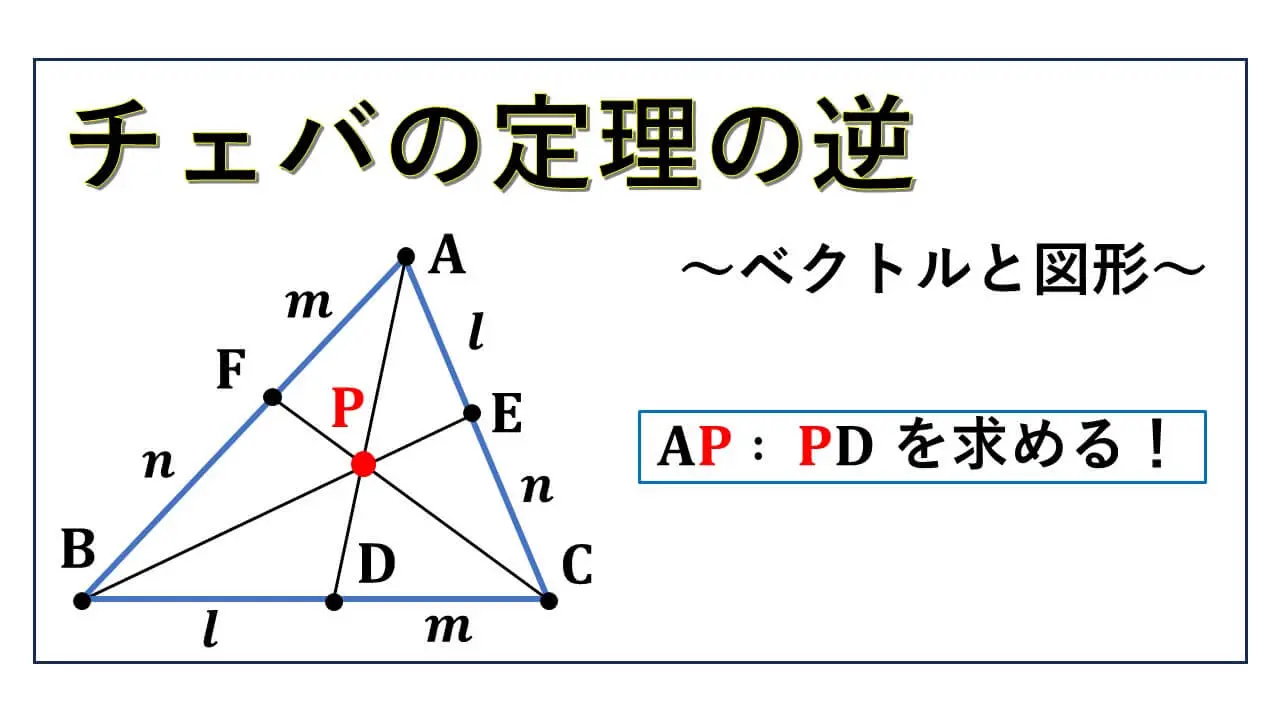
三角形ABC について、辺 BC, CA, AB の上に、それぞれ点 D, E, F をとる。
そして、
BD : DC = l : m,
CE : EA = n : l,
AF : FB = m : n とする。
この状況だと、チェバの定理の逆についての結論以外のすべての状況を満たしています。
命題・仮定・結論についての内容を押さえると、論理を使って、議論を進めることができます。
実際、比率の積が 1 になって仮定を満たしていることを確かめます。
今、BD/DC = l/m,
CE/EA = n/l, AF/FB = m/n となっています。
三つの等式を辺々掛け合わせると、
BD/DC×CE/EA×AF/FB =
l/m × n/l × m/n = 1 です。
これで、チェバの定理の逆の仮定を満たすことが確認できました。
式の計算分野で学習する輪環の順の要領で、三角形を左回りに見ると、うまく比の値の分子と分母が約分されて 1 になるというわけです。
よって、3 本の直線 AD, BE, CF は 1 点で交わるという結論に辿り着きます。
この 1 点を P と置くことにします。
ここからは、メネラウスの定理とベクトルの分点についての公式を使って、さらに細かく詰めます。
チェバの定理の逆 :さらに定理を
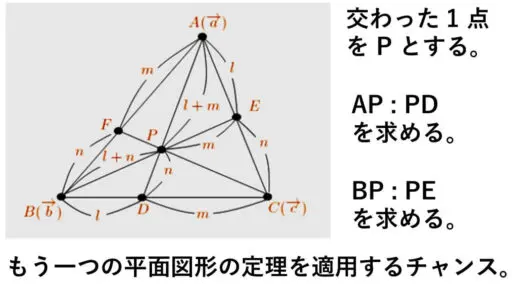
三角形の内部に点 P があります。
さらに、AP : PD という内分比を求めます。
ここで、三角形ADC と直線 BE に対して、メネラウスの定理を適用します。
※ 平行線と線分の比という記事で、この定理の証明を解説しています。
すると、
AP/PD×DB/BC×CE/EA = 1 となります。
BD : DC = l : m,
CE : EA = n : l という状況で議論をしているので、次のようになります。
すなわち、
AP/PD × l/(l+m) × n/l = 1 です。
両辺に逆数を掛け約分をします。
AP/PD = (l+m)/n と、比の値が分かりました。
よって、
AP : PD = (l+m) : n
今度は、BP : PE も求めます。
同様にして比を求める
三角形ABE と直線 FC に対してメネラウスの定理を適用します。
BP/PE×n/(l+n)×m/n = 1 となります。
つまり、
BP/PE = (l+n)/m より、
BP : PE = (l+n) : m となります。
ちなみに、FP : PC も得られます。
三角形AFC と直線 BE に対してメネラウスの定理を適用します。
FP/PC × n/l × (m+n)/n = 1 より、
FP/PC = l/(m+n) となり、
FP : PC = l : (m+n) です。
内分比を求めることができたので、ここからはベクトルの分点公式を使って、位置ベクトル表示を求めます。
チェバの定理の逆 :点Pを位置ベクトルで表示
点 O を三角形ABC の外部にとり、点 A, B, C をそれぞれ位置ベクトルで a, b, c と表します。
これら三つのベクトルを使って、先ほど述べた 1 点で交わった点 P を位置ベクトルで表すことを考えます。
AP : PD = (l+m) : n ということを足掛かりにします。
点 D が関連しているので、先に点 D を位置ベクトルを使って表示しておきます。
BD : DC = l : m だったので、内分点の公式が使えます。
点 D の位置ベクトルを d と置くと、
d = (mb+lc)/(m+l) です。
AP : PD = (l+m) : n なので、
a と d を用いて p を表してから、d を b と c で表します。
点Dをクッションにして計算
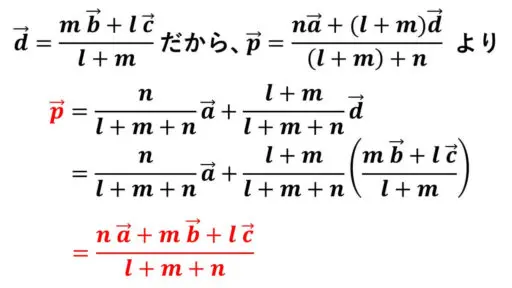
これで、点 P を位置ベクトルで表示することができました。
分母と分子が同じ文字なので、文字の値自体は分かりませんが、約分をすることができるところを約分すると、すっきりとした形になりました。
三角形の三つの頂点の位置ベクトルを用いて、点 P の位置ベクトルを表すことは、重心を位置ベクトルで表示することの一般化にあたります。
l = m = n = 1 のときは、点 D, E, F が三辺の中点になっているときです。
このときは、点 P が三角形の重心になっています。
重心のときは特殊なので、一般の l, m, n についてはチェバの定理の逆を土台にして、点 P の位置ベクトルを導いたというわけです。
チェバの定理の逆から、さらにメネラウスの定理を使うことで、より細かいところまで押さえることができました。
チェバの定理の逆についての証明は、三角形の面積比という記事で解説をしています。
平面図形の内容の復習になり、ベクトルの分点の公式を使う練習にもなるので、今回の内容は高校の数学で広い範囲をカバーします。
関連する記事について
三角形の五心といって、重心の他に、垂心、外心、内心、傍心というものがあります。
傍心は傍接円の中心のことです。
この傍接円という記事でも、図形とベクトルの内容を絡めて、傍心の位置ベクトル表示について解説をしています。
また、三角形は、やはり三角比と関連します。
外心については、外接円という記事で、外接円についての図形内容について解説をしています。
外接円についての図形的な基本は正弦定理に関わるので、しっかりと理解をしておくと良いかと思います。
さらに、直線の傾きに注目をすると、方向ベクトルが重要になります。
図形的な内容とベクトルを関連させて学習をしておくと、様々な場面で役に立ち、高校の数学や物理の学習の支えになってくれます。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。