二直線が垂直 | 傾きの積が-1となる証明【相似で】
二直線が垂直 、このときに、傾きの積がー1となります。
三角形の相似から、図形と方程式の単元で扱われる「垂直に交わる二直線の傾きどうしの積が-1」となることを証明します。
さらに、既に成立している正しい事柄を利用するということについて、ベクトルについても述べています。
それでは、数学IIの内容を相似を使って証明します。
二直線が垂直 :使う相似条件
【三角形の相似条件】
2組の角の大きさがそれぞれ等しい。
他にも三角形の相似条件がありますが、今回のブログ記事の内容では、「二組の角の大きさがそれぞれ等しい」ということを主に使います。
二つの三角形について、頂点どおしの対応、角どおしの対応、辺どおしの対応を正確に押さえることから議論のスタートになります。
ここの対応をまちがうと、議論が曲がってしまうので、この初動は大切になるかと思います。
今回は、高校数学IIで出てくる、垂直に交わる二直線の傾きの積が、-1 となることを証明します。
まずは、たくさんある点の中から、二つの三角形を見つけるところから始めます。
着目する二つの三角形
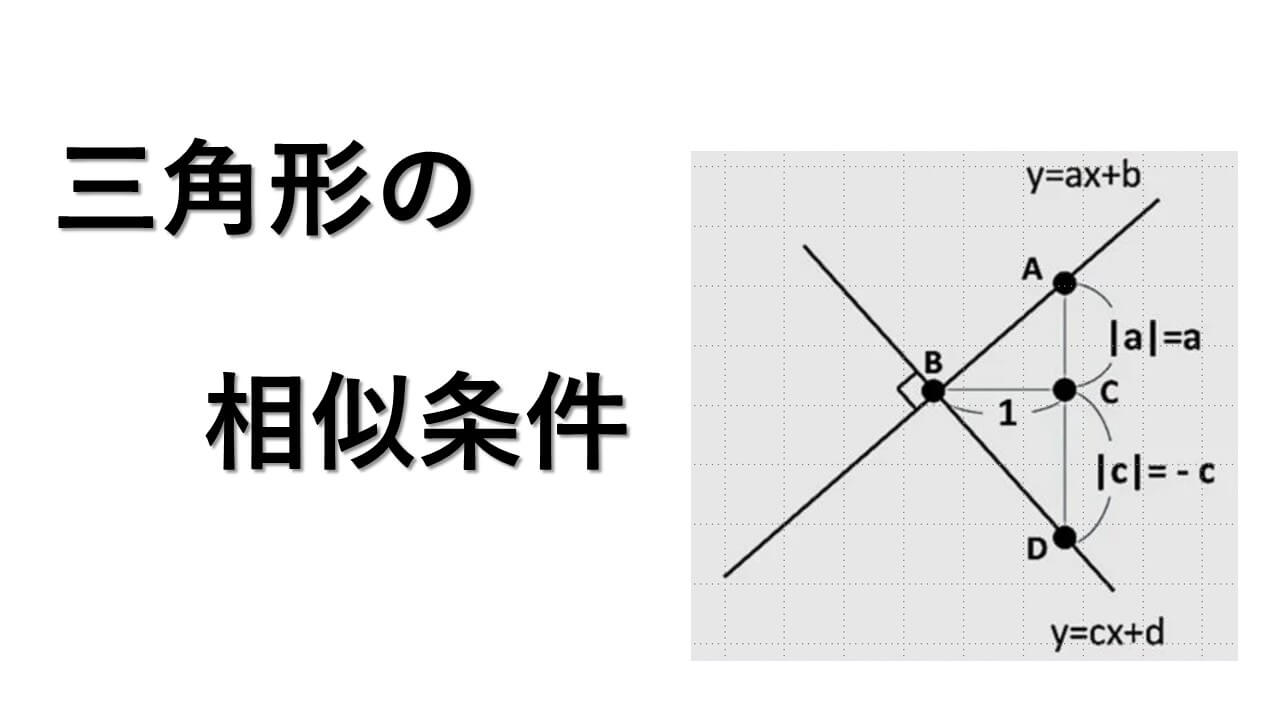
設定とする状況です。
y = ax + b と y = cx + d という二直線が点 B において垂直に交わっていたとします。
このときに、点 B を通り、横軸である x 軸に平行に長さ 1 の線分 BC を補助線として引きます。
そして、点 C を通り BC に垂直な直線を引き、y = ax + b との交点を A とし、y = cx + d との交点を D とします。すると、∠ACB = 90° となっています。
ここで、△ABC と △BDC に着目します。結論から先に述べると、この二つの三角形が相似となります。
理由は、二組の角がそれぞれ等しくなるからです。
二直線が垂直 :傾きの積ー1
<証明>
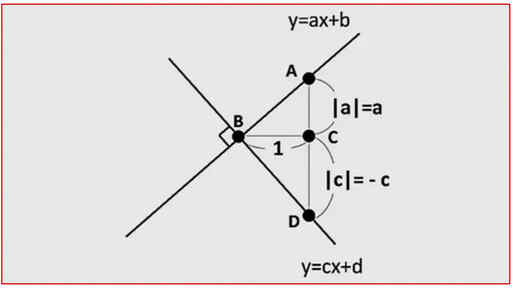
△ABC と △BDC について
∠ACB = ∠BCD = 90° … ①
∠ABC = 90° なので
∠BAC = 90°- ∠ABC … ②
∠DBC = 90°- ∠ABC … ③
②と③について、どちらも同じ大きさに右辺がなっているので
∠BAC = ∠DBC … ④
よって、①と④から二組の角がそれぞれ等しいので、△ABC∽△BDC【証明完了】
ここからは、傾きの積が -1 となることを証明します。
対応する辺の比
相似な三角形について、対応する辺の比が等しいということから、
AC:BC = BC:DC という等式が得られます。
内項の積と外項の積が等しいので、
AC × DC = BC × BC となっています。
ここで、一次関数の変化の割合が傾きである x の係数と同じであるということを利用します。
議論のはじめに引いた補助線 BC の長さを 1 にしておいたので、計算が簡単に運びます。
BC = 1 なので、AC × DC = 1 … ☆
y = ax + b について、x の増加量 BC = 1 に対して、y の増加量を表すのが AC です。
直線の傾き a が変化の割合と等しいので、a と AC ÷ BC が同じ値になり、
a = AC … ⑤ となります。
BC = 1 なので、変化の割合を計算したときに、右辺が AC とシンプルに表せました。
今度はもう一方の直線について、x の増加量を BC = 1 に対する同様の議論を行います。
ただし、図より、DC = |c| = -c となるので注意です。右下がりの直線なので、傾きが負の実数となっているので、絶対値を外したときにマイナスの符号がつきます。
傾き cについて、|c| = DC ÷ BC = DC となり、|c| = -c なので、
-c = DC … ⑥
☆に⑤と⑥を代入すると、a × (-c) = 1
すなわち、ac = -1
これは、二直線 y = ax + b と y = cx + d の傾きの積が -1 ということを示しています。
ベクトルの言葉で表現すると、ベクトル BA とベクトル BD の内積の値が 0 ということになります。
数学IIの図形と方程式の単元ですが、平面ベクトルの内積の定義を使って表現すると議論が進めやすいときもあるので、ベクトルについて言及しました。
平面ベクトルの内積については、リンク先で詳しく解説をしています。
※ 座標を使っての内積の定義もありますが、絶対値と cos を使った内積の定義と値が一致します。状況に応じて、使いやすい方の定義を使えます。
線分比への異なるアプローチ
今、証明した直交する二直線の傾きの積が -1 ということを導くのに、相似比を利用しました。
ただ、高校の数学になると、線分比を求めるときに、三角形の相似とは異なる求め方をするときがあるので注意です。
その代表的な求め方が、メネラウスの定理であったり、チェバの定理です。
これらは、中学受験の算数の問題では、難しい内容として位置づけられていますが、高校の平面図形の単元で学習をして、定期考査には出題頻度が高いものになります。
そのため、大学受験で使えるときには、メネラウス(チェバ)の定理を使って、効率よく線分比を求めることが大切になってきます。
さらに、ベクトルも合わせて使えると、図形問題を解くための大きなノウハウとなります。
平面図形の性質と図形と方程式、そしてベクトルの理解がつながると、解法のバリエーションが充実するかと思います。
二直線が垂直 【関連】中点連結定理
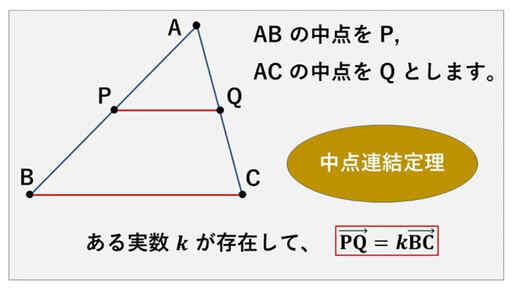
三角形の相似条件に、「1 組の角とその間の比がそれぞれ等しい」というものがあります。この相似条件を利用するのが、中点連結定理です。
図で、点 P と点 Q がどちらも辺 AB と辺 AC の中点なので、
AP : AB = 1 : 2,
AQ : AC = 1 : 2
∠ A は共通の角より △APQ ∽ △ABC となります。
そのため、対応する角の大きさが等しいので、
∠APQ = ∠ABC です。
これは、同位角が等しいということなので、直線 PQ と直線 BC が平行ということになります。
ここまでが、中学の数学で学習する中点連結定理です。
この定理は、高校の平面図形でも出てきます。注意点として、ベクトルを使って内容を表現するときです。
高校の数学では
中学の数学では、中点連結定理より、「PQ と AB が平行」という言い方をします。
この内容をベクトルを使って表すと、中点連結定理より、「ベクトル PQ とベクトル BC が平行」ということになります。
さらに、二つのベクトルが平行ということは、片方を適切に実数倍すると、もう片方に一致することです。
そのため、ある実数 k が存在して、ベクトル BC の k 倍がベクトル PC に等しいということになります。
これが、先ほどの図の右下に書いている式です。中点連結定理から、すぐにベクトルを実数倍した等式が書かれることもあるので注意です。
ちなみに、ある実数 k と書きましたが、相似比が 1 : 2 になっていたので、k の値は 1/2 ということです。
図形的に、線分 BC を半分の長さに縮小すると線分 PC の長さに等しいということも表します。
ここまで、三角形の相似を中心に述べてきました。以下で、三角形の合同に注目した内容を述べています。
二直線が垂直【関連2】ベクトルも考察
垂直に交わる二直線の傾きの積が -1 となるということを、ベクトルを使って考えてみます。
y = (-3/5)x+2,
y = (5/3)x+4
この二つの関数の式で表される二直線は、垂直に交わっています。
-3/5 × 5/3 = -1 というように、傾きの積で垂直に交わっているのかどうかを判断することができます。
ここで、直線の傾きを変化の割合で考えてみます。すると、方向ベクトルが分かります。
y = -3/5x + 2 だと、
x 軸方向に(右方向に)5 進むと、y 軸方向に(縦軸方向に)-3 進むということです。
この変化の割合をベクトルで表すと、x 成分が 5 で y 成分が -3 ということです。
つまり、ベクトル (5, -3)
y = 5/3x + 4 についても、同様にして、ベクトル (3, 5) が方向ベクトルだと分かります。
これら二つの直線の傾きに相当する方向ベクトルについて、内積を計算してみます。
(5, -3)・(3, 5)
= 5 × 3 + (-3) × 5 = 15 - 15 = 0
方向ベクトルどおしも内積を計算すると値が 0 になっているので、垂直に交わっていることが分かりました。
このように、直線の傾きを方向ベクトルで考えるときもあります。
【関連する記事】
平面図形については、
方べきの定理を相似を用いて証明をしています。
また、垂直二等分線について、三角比と関連する内容として外接円があります。三角比(三角関数)との関連ということで、中学の数学の内容と合わせて基礎を論理的に把握しておくと良いかと思います。
さらに、今回の内容を直線のベクトル方程式の議論へと広げた記事も投稿しています。
方向ベクトル-法線ベクトルという記事で、平行条件や垂直条件を満たす直線の方程式を求める理論を解説しています。
ちなみに、中学の数学の内容について、
比の相等という記事でも、三角形の相似を利用した内容を解説しています。
それでは、今回のブログ記事をこれで終了します。
読んで頂き、ありがとうございました。