内積の定義 | 二つの定義は同じ値になる【高校で学習する平面ベクトル】
高校数学で学習する平面ベクトル (plane vector) の「 内積の定義 」について解説をしています。
ベクトルの長さ（大きさ）や成分表示と関わってくる基本ベクトルをしっかりと認識することが大切になるかと思います。
高校数学の平面ベクトルの理解をしつつ、大学数学のベクトル空間論の基底の具体例を知ることにもなります。xy 座標平面からスタートできるので、勉強しやすいかと思います。
ただ、ベクトルを学習し始めたときに、内積の定義が二つあり、どちらも使われます。
この疑問を早い段階で解消できると、気分よくベクトルの学習ができた経験から、私と同じ様に困惑される方の疑問の解消になれば幸いです。
このブログでは、高校数学で学習する平面ベクトルを具体例を通じて解説していきます。
大学や専門学校で学習する線形代数学のベクトル空間論へつながる内容にも触れています。
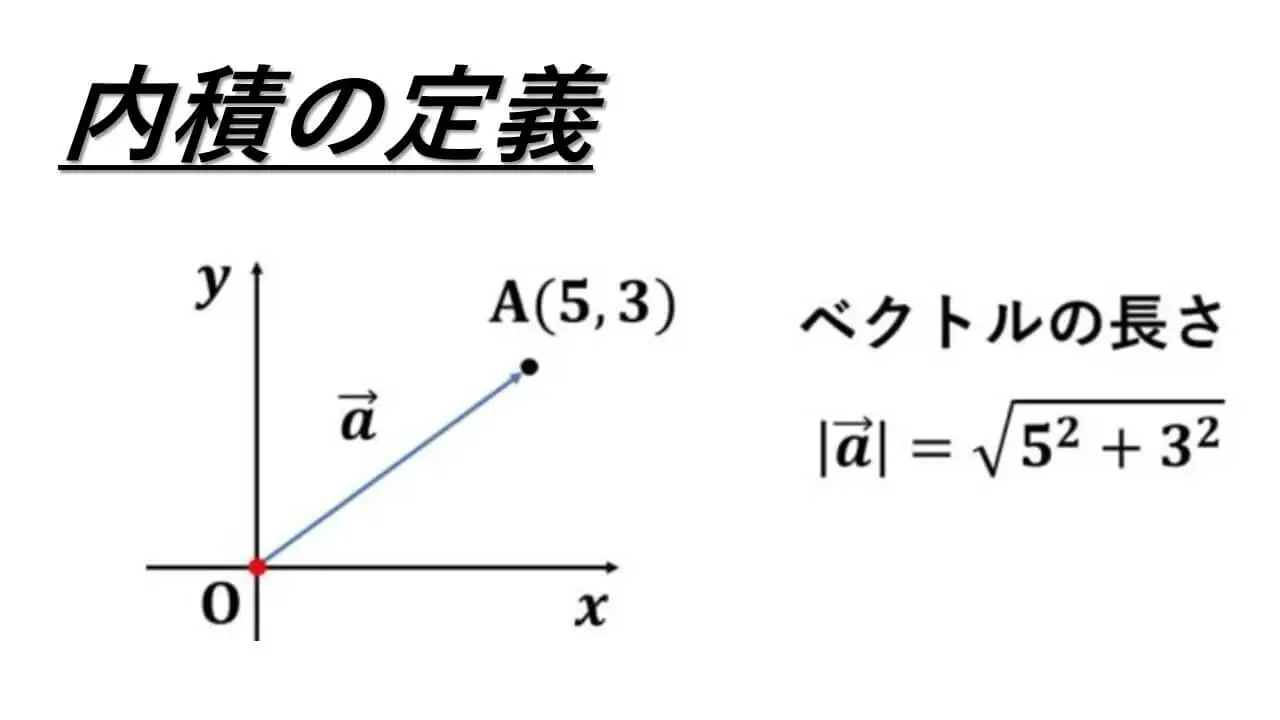
内積の定義 :長さと成分
xy-座標平面上の原点 O(0, 0) と、
点 A(5, 3) について、原点を始点とするベクトルOAを考えます。
このベクトルOAの終点は、点 A(5, 3) です。
このときに、位置ベクトルとして小文字でベクトル a と表記されることもあります。
位置ベクトルというと、高校数学の用語で難しく感じるかもしれませんが、原点 (0, 0) を始点とするベクトルです。
終点が点 A のときに、小文字で a と表すということです。
OA = a = (5, 3) を成分表示といい、5 を x 成分、3 を y 成分といいます。
ここで大切なことは、x 軸と y 軸という直交座標で平面ベクトルを(5, 3) のように表すときに、原点 (0, 0) を始点として考えているということになります。
このことを押さえておくと、ベクトルOAにせよ、位置ベクトル a にせよ、座標平面において平面ベクトルを使えます。
平面ベクトルの長さ
平面ベクトルには、向きと長さがあります。向きは始点から終点へ向けての矢印です。
ここで、ベクトルの長さ（大きさ）のことを計算するときに、ピタゴラスの三平方の定理を使います。
記号 | □ | を使って、ベクトルOA もしくは、位置ベクトル a の長さを表します。
終点である点 A の座標が (5, 3) のときは、中学数学で学習した三平方の定理を使って、5 の 2 乗と 3 の 2 乗の和にルートをつけると長さが求まります。
※ 答案の答えを書くときには、ルートを簡単な形に直して提出します。
平面ベクトルの成分
xy 座標平面上の点 A の座標 (5, 3) について、5 を x 座標の値、3 を y 座標の値といいます。
数学2 を学習しているときには、x 座標や y 座標というのですが、ベクトルOA（位置ベクトル a）の議論をしているときには、x 成分が 5 で、y 成分が 3 のベクトルといいます。
成分は、英語で書くと component です。まさに、構成している「成分」というわけです。
では、二つの内積の定義について解説します。
内積の定義 :二つの定義で同じ値
内積には、図に書いた「定義 1」と「定義 2」があります。
実は、xy 座標軸が導入されているときに、どちらも同じ値になるということが証明できます。
この二つは、余弦定理の等式を同値変形で書き換えることで結びつきます。
先ほどの図について、
余弦定理より、
AB2 = OA2+OB2－2OA・OB・cos θ です。
OA = |OA| = |a|,
OB = |OB| = |b|,
AB = |AB| = |b－a| なので、
|b－a|2 = |a|2+|b|2－2|a||b|cos θ を得ます。
xy 座標平面において、原点 O(0, 0) を位置ベクトルの基準（始点）として、図のように位置ベクトル表示をします。
線分の長さをベクトルの大きさ（長さ）を使って表すと、太字をつけた等式に書き換えられます。
この等式で、絶対値の二乗の部分を、成分を使って表すようにします。
この成分は、はじめの図の点 A と点 B の座標として使われていた値です。
余弦定理から同値変形
|b－a|2 = |a|2+|b|2－2|a||b|cos θ,
b－a = (x2－x1, y2－y1) より、
(x2－x1)2+(y2－y1)2 =
x12+y12+x22+y22－2|a||b|cos θ
左辺を展開し、右辺の二乗の項を左辺へ移項します。
すると、
－2x1x2－2y1y2 = －2|a||b|cos θ
つまり、
|a||b|cos θ = x1x2+y1y2 を得ます。
この等式は、「定義 1」と「定義 2」が同じ値ということを表しています。
この考察から、空間座標で内積を考えるときも、余弦定理から同様にして、二つの内積の定義が同じ値になっていることが導かれます。
空間ベクトルのときは、z 成分があるので、その分だけ項が増えるだけで、同様の証明になります。
a = (x1, y1, z1),
b = (x2, y2, z2) とし、なす角を θ とします。
|b－a|2 = |a|2+|b|2－2|a||b|cos θ,
b－a = (x2－x1, y2－y1, z2－z1) より、
(x2－x1)2+(y2－y1)2+(z2－z1)2 =
x12+y12+z12+x22+y22+z22－2|a||b|cos θ
左辺を展開し、右辺の二乗の項を左辺へ移項します。
すると、
－2x1x2－2y1y2－2z1z2 = －2|a||b|cos θ となります。
つまり、
|a||b|cos θ = x1x2+y1y2+z1z2 を得ます。
これで、平面ベクトルと空間ベクトルの内積が定義できたので、これを使って、さらに解説を進めます。
「定義 1」 と「定義 2」が、どちらも同じ値になるということは、状況に応じて、適した方に書き換えができるので便利です。
座標から内積がとる実数値を「定義 2」で計算して、値が 0 になっていたとします。
二つのベクトルが 零ベクトルでないときには、cosθ = 0 ということになり、なす角の定義 0 度から 180 度ということから、θ が 90 度ということになります。
これは、「二つの零ベクトルではないベクトルどおしの内積値が 0 と」と、「二つの零ベクトルではないベクトルが垂直であるということ」が同値（必要十分条件）であるということです。
空間ベクトルの成分表示について、次の基本ベクトルは大切になります。
空間ベクトルより
xy 座標平面は、二つの垂直に交わる軸で構成されています。
平面ベクトルの成分を考えるときにも、大切な基本ベクトルという長さが 1 の単位ベクトルがあります。
単位ベクトルとは、長さが 1 のベクトルということです。
特徴的な単位ベクトルとして、
e1 = (1, 0), e2 = (0, 1) があります。
これら二つのベクトルを実数倍したベクトルを足し合わせることで、平面ベクトルたちを表すことができます。
ベクトルの実数倍
p と q を実数として、基本ベクトルを実数倍してみます。
pe1 = (p, 0), qe2 = (0, q) となります。
ベクトルの実数倍とは、x 成分と y 成分のどちらにも、その実数を掛けます。
基本ベクトルについては、もう片方の成分が 0 となっているので、1 という値が拡大縮小することになります。
そのため、方向がプラスとマイナスで反転することはあっても、同じ軸上のベクトルということになります。
ベクトルの加法
pe1 + qe2 = (p, q) となります。この実数倍したベクトルたちで加法をとることを一次結合といいます。
先ほどの点 A(5, 3) について、ベクトル a を基本ベクトルを使って表すときには、p = 5, q = 3 とします。
5e1 + 3e2
= (5, 0) + (0, 3)
= (5, 3)
それぞれの基本ベクトルを実数倍をしたベクトルはどうなるのかをまず押さえます。
そして、実数倍された ベクトルたちで加法を計算します。
その結果、先ほどのベクトル a が、基本ベクトルの一次結合で表されたということになります。
内積の定義 :集合も考える
{(p, q) | p, q は実数} は平面ベクトル全体となります。原点を始点とする平面ベクトルをすべて集めた集合です。
※ 要素（元）というブログで集合の表し方を説明しています。
この集合は、大学や専門学校で学習する線形代数学では、2 次元ベクトル空間といわれます。
※ 先ほどの実数倍を実数体からのスカラー倍、そして平面ベクトルの加法について、ベクトル空間の公理に当てはまります。
{(p, q) | p, q は実数} に含まれている平面ベクトルは、先ほどの基本ベクトルの一次結合で表されます。
そのため、{pe1 + qe2 | p, q は実数} が平面ベクトル全体となります。
線形代数学の言い方をすると、2 次元ベクトル空間は、基本ベクトルの一次結合で表されるベクトル全体と一致するということです。
しかも、基本ベクトルは、次の一次独立の定義も満たします。
一次独立性について
「pe1 + qe2 = (0, 0) ただし、p, q は実数 」とすると、p = 0 , q = 0 となります。
零ベクトルを一次結合で表す表し方が、実数倍の部分がすべて 0 になっている一次結合しかあり得ないということです。これが、一次独立の定義です。
一次独立であって、しかも、それらの一次結合で表されるベクトルの集合が、全体集合であるベクトル空間と一致するときに、基底といいます。
{e1, e2} が 2 次元ベクトル空間である平面ベクトル全体の基底となります。基底という集合に含まれているベクトルの個数が 2 個なので、2 次元といいます。
ちなみに、空間ベクトルだと、(p, q, r) という形になります。平面ベクトルよりも成分が 1 つ増えています。そのため、基本ベクトルがもう一つ増えます。
(0, 0, 1), (0, 1, 0), (0, 0, 1) が空間ベクトルについての基本ベクトルとなります。空間ベクトルは、3 次元ベクトル空間となっています。
そして、これら三つの基本ベクトルから成る集合が、基底となります。
平面ベクトルについて、基底を構成するベクトルの個数が 2 個なので、2 次元と述べました。
空間ベクトルについても、基底を構成するベクトルの個数が 3 個なので、3 次元です。
内積の定義 :基本ベクトルは直交
高校数学を学習するときに、二つのベクトルが直交する（垂直に交わる）ということを調べるのに、内積をよく使います。
内積を計算して、値が 0 になっているときに、二つのベクトルが直交していると判断をするわけです。
※ ただし、どちらも零ベクトルではないときの話です。
e1 = (1, 0) と e2 = (0, 1) は直交しています。実際に内積を計算してみます。
e1・e2 = 1 × 0 + 0 × 1 = 0
x 軸上に乗っている e1 と y 軸上に乗っている e2 ですから、なす角が 0°になっているということが視覚的にも分かりますが、内積も計算してみました。
垂直ではないベクトル
高校数学で学習する平面ベクトルでは、どちらも零ベクトルではないベクトルで、平行になっていないときに、それら二つのベクトルが一次独立ではないということを学習します。
先ほど、少し触れたのですが、2 次元ベクトル空間である平面ベクトル全体は、2 個の一次独立なベクトルで基底が構成されていました。
抽象論はさておき、結果だけを述べることにします。
有限次元ベクトル空間の基底を構成するベクトルの個数は一定です。
そして、実際に基本ベクトル 2 個が基底になっていることから、平面ベクトル全体は 2 次元です。
2 個の一次独立なベクトルの一次結合で表されない平面ベクトルが存在したとすると、3 個の一次独立な平面ベクトルができてしまいます。
これは、上で紹介した一次独立なベクトルの最大個数が、そのベクトル空間の次元以下であることに矛盾してしまいます。
それゆえに、直交していなくても、零ベクトルでなく互いに平行ではない平面ベクトル 2 個で、基底を作れるということになります。
今回のブログ記事では、内積の定義と垂直という内容を中心に説明をしました。
斜めに交わるベクトルについての内容と合わせることで、ベクトルについての基本がしっかりと確立するかと思います。
最後に、参考として大学の線形代数学で扱われる内積に関わる内容を述べておきます。
グラム・シュミットの直交化法
【定義】
V を内積が定義されている複素数体 C 上のベクトル空間とします。
また、{x1, … , xn} を V の基底とします。
この基底が次を満たすときに、V の直交基底といいます。
＜xi, xj＞ = δij（ただし i, j = 1, … , n）
この δij はクロネッカーのデルタといって、i と j が等しいときは値が 1 で、i と j が異なるときは値が 0 となっています。
グラム-シュミットの直交化法を使うことで、与えられた基底から、互いに異なる基底どおしの内積が 0 となっている基底を作り出すことができます。
このブログ記事で用いる記号ですが、
v ∈ V に対して、||v|| でそのノルムを表しています。
ここからは、二つのベクトル u, v について、
<u, v> で内積を表すことにします。
(<v, v>)1/2 が ||v|| というノルムの値です。
つまり、自身との内積値にルートをつけたものがノルムです。
大学の数学科の一年の内容なので難しいですが、理論の理解が必要な方に向けて、ここからは述べる内容となります。
直交化の操作について
{v1, … , vn} を内積＜・, ・＞が定義されているベクトル空間 V の基底とします。
基底を構成する各ベクトルはベクトル空間の加法についての零ベクトル o ではないので、各 vk は零ベクトル o とは異なっています。
この与えられた基底について、まず v1 から大きさ 1 のベクトル e1 を作ります。
それから、 ＜a2, e1＞= 0 を満たすベクトル a2 を作ります。内積を取ると値が 0 ということで、e1 と a2 が直交しているということです。
e1 と a2 の作り方は次の通りです。
e1 := v1/||v1|| と置きます。
また、
a2 := v2－<v2, e1>e1 と置きます。
この a2 は、
<a2, e1> = 0 を満たします。
さらに、e2 := a2/||a2|| と置きます。
v1 ≠ o なので、内積の定義からノルム ||v1|| は 0 ではありません。
※ この 0 は複素数の 0 です。
※ e1 の作り方は、高校のベクトルで学習した大きさ 1 のベクトルにする方法です。
上のように a2 を定めると、e1 との内積の値が 0 となることが分かります。
実際に＜a2, e1＞ = 0 となることを確かめてみます。
実際に＜a2, e1＞ = 0 となることを確かめてみます。
＜v2 － ＜v2, e1＞e1, e1＞
= ＜v2, e1＞ － ＜v2, e1＞＜e1, e1＞
= ＜v2, e1＞ － ＜v2, e1＞ = 0
＜e1, e1＞ = 1 となるように e1 を定めておいたことが効いています。
さらに、上のように a2 の大きさを 1 にするように e2 を定めると、
1 / ||a2|| がスカラー倍として内積の外に出せるので、
＜e1, e2＞ = ＜e2, e1＞ = 0
これで、e1, e2 という大きさ 1 のベクトルで、互いに内積が 0、つまり直交しているベクトルを作ることができました。
さらに順番に大きさが 1 で、互いに直交するベクトルたちを定義していきます。
三つ目のベクトル e3 を定義するために、まず a3 を
v3 －＜v3, e1＞e1－＜v3, e2＞e2 と定めます。
ちょっと長いですが、これがベクトル a3 です。
先ほどと同様に、a3 を単位化して大きさを 1 としたベクトルを e3 とします。
a4 も同様に定義して、それを単位化することで e4 とします。
この繰り返しで、最終の an は
vn-＜vn, e1＞e1-＜vn, e2＞e2
– … -＜vn, en-1＞en-1 となります。
この an を単位化して、en とします。
すなわち、
en := an/ ||an|| です。
{e1, e2, … , en} が V の正規直交基底となっています。
つまり、それぞれが大きさ 1 のベクトルで、添え字が異なるベクトルどおしの内積値が 0 となっています。
{v1, … , vn} という与えられた基底から、新しく正規直交基底を作る一連の上で述べた手順がグラム-シュミットの直交化法です。
後、内積が定義されているベクトル空間において、役に立つ命題を一つ紹介します。
大学での命題の証明
【命題】
V を内積が定義されている複素数体上のベクトル空間とします。
v1, … , vn を零ベクトル o ではない V の元たちとします。
そして、dim V = n、つまり V の次元を n とします。
このとき、もし ＜vi, vj＞ = δij (i, j = 1, … , n) とするならば、
{v1, … , vn} は V の基底です。
＜証明＞
内積の値がクロネッカーのデルタとなっていることから、v1, … , vn が線形独立だということを示せます。
c1v1 + … + cnvn = o (各 ck ∈ C) とします。
このとき、 vi との内積を考えます。
【左辺について】
＜c1v1, vi＞ + … +＜civi, vi＞+…
…+ ＜cnvn, vi＞
= c1δ1j + … + ciδii + … + cnδni
= 0 + … + ci × 1 + … + 0
= ci
【右辺について】＜o, vi＞ = 0
よって、ci = 0 ( i = 1, 2, … , n) となります。
これは、v1, … , vn が線形独立ということを示しています。
dim V = n なので、{v1, … , vn} は V を生成しなければなりません。
ゆえに、基底となっています。【証明完了】
大学の線形代数学については、
無限次元ベクトル空間-例-実数列という記事などを投稿しています。
ちなみに、１つ前の記事は高校数学の内容となっています。
それでは、これで、今回のブログを終了します。
読んで頂き、ありがとうございました。