三平方の定理 | 証明を中学で習った内容で理解し、余弦定理への拡張という広がりを知る
「 三平方の定理 」の証明を中学の数学で学習します。
その証明を通じて、既に成立している定理を拡張させるという数学においての発想を垣間見ることができるピタゴラスの定理です。
三平方の定理(ピタゴラスの定理)は、直角三角形のとき限定で使える定理です。
高校の数学では、直角三角形以外の一般の三角形について、適用できる三平方の定理の拡張となる余弦定理を学習します。
そうした数学のつながりを意識するのに、良い内容かと思います。
さらに、三平方の定理の証明で使う発想から、大学の数学の代数分野の内容をピックアップしています。
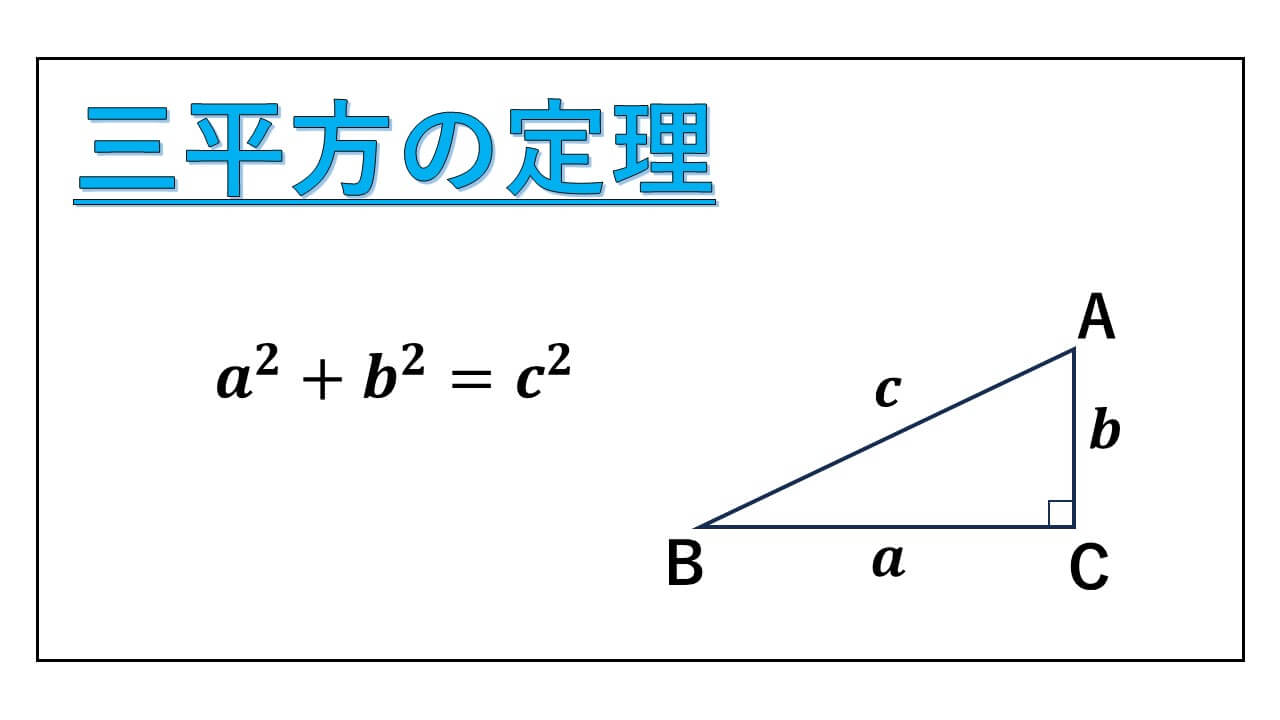
サムネイルの図に描いている直角三角形は、三角定規でお馴染みの形です。
これと合同なぴったり重なる三角定規を 4 個使って、大きな正方形を作ります。
三平方の定理 – 証明 :図形的に
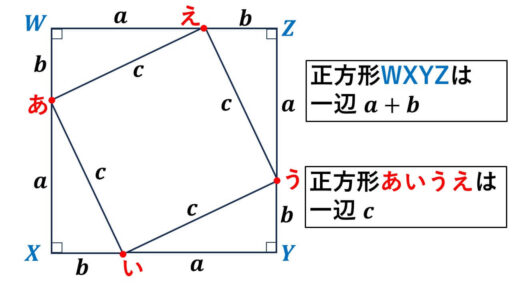
∠BCA が 90° で斜辺の長さが c となっている直角三角形を 4 個を貼り合わせました。
すると、「正方形WXYZ」となります。
その中に、「正方形あいうえ」ができています。
面積のことを考えると、
「正方形WXYZ」の面積から、4 つの合同な直角三角形の面積を引くと、「正方形あいうえ」の面積となります。
なぜ正方形と断定できるかというと、4 つの辺の長さがすべて等しい四角形だからです。
公立の中学だと、中学2年の数学で学習する内容で、「四角形の 4 つの辺の長さが全て等しいとき、その四角形は正方形である」という命題があります。
この正しい(真である)命題を適用しました。
※ 命題-仮定-結論という記事で、高校数学や大学の数学で基本となる命題と論理について解説をしています。
「四角形WXYZ」だと、4 つの辺の長さが、どれも a+b となっています。また、「四角形あいうえ」については、どの辺も長さが c となっています。
そのため、どちらの四角形も、正方形だと決定できます。
三平方の定理は、a2+b2 = c2 という三角形の三辺の長さについての等式です。これを証明するために、正方形の面積を考えます。
図形の面積と展開公式
「正方形WXYZ」の面積は、一辺の長さが a+b ということから、縦と横の長さを掛け算することで求まります。
(a+b)×(a+b) = (a+b)2
= a2+2ab+b2 が、「正方形WXYZ」の面積です。
二乗の展開公式を使いました。このように、数学では証明しようとしている命題の真偽に関わりなく既に成立している命題を適用することができます。
※ ちなみに、三乗和の公式という記事で、高一で学習する三乗の展開公式や、因数分解公式を解説しています。
また、直角三角形の面積は、底辺が b で、高さが a なので、
b × a × 1/2 となります。
そのため、合同な 4 個の直角三角形の面積の和は、1 つの直角三角形の面積の 4 倍となります。
すなわち、
b × a × 1/2 × 4 = 2ab が、4 個の合同な直角三角形の面積の和です。
「正方形WXYZ」の面積から、4 個の合同な直角三角形の面積の和を引いた残りが、「正方形あいうえ」の面積である c2 なので、次の等式が得られます。
c2 = (a+b)2-2ab
= a2+2ab+b2-2ab
= a2+b2
これで、三平方の定理が証明できました。
まとめ
【三平方の定理】
三角形ABCを∠BCA = 90° の直角三角形とし、
BC = a, CA = b, AB = c とする。
このとき、a2+b2 = c2 である。
図形の面積と、計算の公式を関連させて証明をすることができました。
ここで、三角形の頂点と辺の長さについて、次の表し方を覚えておくと、高校数学の三角比の学習で役に立ちます。
頂点 A と向かい合う辺 BC の長さを A の小文字で a と表します。
視点を変えて、頂点 B に向かい合う辺は、CA で、その長さを b と表します。
頂点 C と向かい合う辺は、AB で、AB の長さが c です。
直角三角形については、直角と向かい合う斜辺の長さが、三辺の中で一番長くなっています。
今、証明した三平方の定理は、直角三角形のとき限定で使える定理です。
そこで、∠BCA が直角でない三角形についても使える定理がないかと考えます。
∠BCA が 90° のときには、三平方の定理と同じ等式になり、90° でないときにも成立する等式が得られると、定理の適用範囲が広がります。
この意味で三平方の定理の拡張となる定理を紹介します。高校数学の三角比の内容となります。
三平方の定理 :定理の拡張
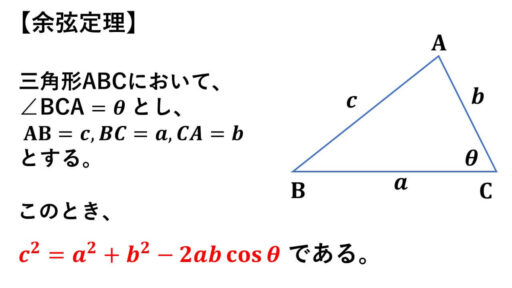
これが、高校一年の三角比の単元で学習する余弦定理です。
θ = 90° のとき、
cos 90° = 0 なので、
c2 = a2+b2 となり、三平方の定理の通りです。
三角形の一つの内角の大きさは、
0° よりも大きくて、180° より小さいので、
0° < θ < 180° となっています。
90° のときは、三平方の定理と一致していて、内角の大きさが、それ以外のときでも成立することから、三平方の定理の拡張となっています。
このように、数学では、一つの命題が成立したときに、命題を改造して、より広い範囲に適用できる命題を更に導けないかと考えるときもあります。
直角三角形について適用できる三平方の定理を、直角が無い三角形にも適用できるように拡張した定理が、余弦定理です。
余弦定理の証明
θ = 90° のときは、先ほど述べたように三平方の定理より成立しています。そのため、θ が鋭角のときと、鈍角のときに場合分けをして証明します。
sin2θ+cos2θ = 1 という三角比で学習する基本的な公式を使います。
【θ が鋭角のとき】
点 A から辺BC に垂線を引き、その交点を H とします。
すると、三角形AHC において、AC が直角と向かい合う斜辺となります。
三角形AHC について、三角比の定義から、
AH = AC × sin θ
= bsin θ … (1)
CH = AC × cos θ = b × cos θ
よって、
BH = BC-CH
= a-bcos θ … (2)
三角形ABH は、AB が直角と向かい合う斜辺となっています。
三角形ABH に三平方の定理を適用すると、
AB2 = BH2+AH2 … (3)
(1) と (2) を (3) に代入すると、
c2 = (a-bcos θ)2+(bsin θ)2
= a2-2abcos θ+b2(sin2θ+cos2θ)
ここで、sin2θ+cos2θ = 1 なので、
c2 = a2-2abcos θ+b2 となります。
すなわち、
c2 = a2+b2-2ab×cos θ となります。
これで、θ が鋭角のときに、余弦定理が成立することが証明できました。
【鈍角のとき】
θ が鈍角のときは、点 A から半直線BC の延長へ垂線を引き、その交点を H とします。
三角形ACH が、∠CHA = 90° の直角三角形です。そのため、この三角形においては、AC が斜辺となっています。
∠ACH = 180°-θ です。
三角比の定義から、
AH = AC × sin(180°-θ)
= bsin θ … (4)
三角比の相互関係から、
sin(180°-θ) = cos θ となることを使いました。
また、三角比の定義から、
CH = AC × cos(180°-θ)
= -bcos θ です。
そのため、
BH = BC+CH
= a-bcos θ …(5)
三角形ABH は、AB を斜辺とする直角三角形です。
三角形ABH に三平方の定理を適用すると、
AB2 = AH2+CH2 … (6)
(6) に (4) と (5) を代入すると、
c2 = b2sin2θ+(a-bcos θ)2
= a2-2abcos θ+b2(sin2θ+cos2θ)
= a2+b2-2abcos θ
これで、鈍角のときにも余弦定理が成立することを示せました。
鈍角のときは、180°-θ についての三角比の相互関係を利用することと、サインの二乗とコサインの二乗の和が 1 となるということを利用する証明でした。
※ 正弦定理の証明はリンク先の記事で述べています。
三平方の定理の拡張が余弦定理ということで、鋭角のときにも鈍角のときにも、既に証明していた三平方の定理を使いました。
三平方の定理の逆
三角形ABC について、
a2+b2 = c2 ならば、∠BCA = 90° になっています。
着目している角の大きさが 90° かどうかということを三辺の長さから計算で判断することができるというのが、三平方の定理の逆です。
余弦定理を使って、三平方の定理の逆を証明します。
∠BCA = θ とします。
三角形の一つの内角の大きさなので、
0° < θ < 180° です。
仮定より、c2 = a2+b2 です。
一方、余弦定理より、
c2 = a2+b2-2ab×cos θ です。
c2 = a2+b2 を左辺に代入すると、
a2+b2 = a2+b2-2ab×cos θ です。
移項すると、
2ab×cos θ = 0 です。
辺の長さは 0 より大きいため、
a ≠ 0, b ≠ 0 です。
よって、cos θ = 0
0° < θ < 180° の範囲で考えているので、
cos θ = 0 となるのは、
θ = 90° のときのみです。
よって、90° = θ = ∠BCA が示せました。
三平方の定理の逆を証明したときの計算で、コサインの値が有名角のときの値になっているときは、三角比の表なしで、角の大きさを余弦定理から計算できます。
これは、高校の数学の三角比の単元で、よく使う内容になります。
ここからは、余弦定理を使う練習問題です。
三平方の定理から余弦定理へ
【問題1】
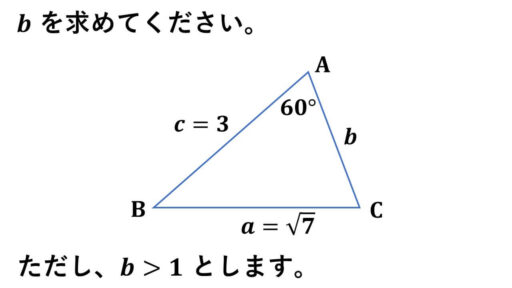
CA = b の値を求める問題です。
b > 1 という内容も使うことになるときもあるかもしれないという内容になっています。
角 A の大きさが 60°と分かっているので、角 A に着目した余弦定理の式を使います。
a2 = b2+c2-2bc・cos A に分かっている値を代入します。
ルートは二乗すると外れるので、左辺は 7 となります。
7 = b2+32-2b・3・cos 60° となります。
さらに、cos 60° = 1/2 なので、計算を進めることができます。
7 = b2+9-3b となるので、移項して整理し、b についての二次方程式を降べきの順に左辺に記します。
b2-3b+2 = 0 となります。
この左辺ですが、因数分解ができます。
(b-1)(b-2) = 0 となります。
よって、b = 1, 2 となります。
ここで、b > 1 という条件を使います。
b = 1 は、この条件に合わないので不適とします。
ゆえに、b = 2 となります。
これで、求めたかった CA の長さが 2 と分かりました。
この【問題1】のように、高一の一学期に学習した計算が必要になります。
普段から計算規則に基づいて、三角比を学習しつつ、計算の力を鍛えておくと良いかと思います。
今の問題は、図がありましたが、高校の数学では、図が与えられていない問題も出題されることが多いです。
図が無いときこそ、三つの頂点を左まわりに考えて、頂点の位置にある角と、角に向かい合う小文字で記す辺の長さを正確に設定することが大切になります。
どの辺の文字かを把握
【問題2】
三角形 ABC に関して、
AB = 3, CA = 4,
A = 60° とします。
このとき、BC の長さを求めてください。
頂点 A から左まわりに、頂点 B と頂点 C が配置されていると考えます。
そうすると、頂点 A に向かいあう辺は BC となります。
また、頂点 B に向かいあうのが CA で、頂点 C に向かいあうのが AB です。
そのため、a = BC,
b = CA = 4, c = AB = 3 と小文字で辺の長さを表します。
頂点 A の大きさが分かっているので、A に向かいあう辺の長さ a が左辺に現れる余弦定理の式を使います。
a2 = b2+c2-2bc・cos A に分かっている値を代入します。
cos 60° = 1/2 なので、
a2 = 52+42-2・5・4×(1/2) となります。
つまり、
a2 = 25+16-20
= 21 です。
よって、a = (21)1/2 となります。
辺の長さは正の実数となるので、21 の正の平方根なので、ルート 21 が答えとなります。
余弦定理に慣れるためには、どの辺の長さをどの小文字で表しているのかを正確に把握することが大切になります。
三角比の単元は、中学の数学で学習した図形の内容や比の内容が関わってきます。
余弦定理の式の書き換え
a2 = b2+c2-2bc・cos A という頂点 A の部分の角に着目した等式について、式を変形した公式を導きます。
2bc・cos A は、少し長いですが掛け算だけの式なので、単項式となっています。
この固まりを左辺に移項します。
そして、a2 を右辺へ移項します。
すると、
2bc・cos A = b2+c2-a2 となります。
さらに、2bc で両辺を割ると、
cos A = (b2+c2-a2)÷(2bc) です。
この式だと、cos A の値が右辺の値という意味になります。
そのため、A という角の大きさが三角比の表から分かるという式になっています。
A に着目した式ですが、B や C に着目して、同様の式の書き換えをすることもできます。
cos B = (c2+a2-b2)÷(2ca),
cos C = (a2+b2-c2)÷(2ab) となります。
三角形が出てきたときに、このように順に文字を入れ替えた式が同様に導けるときが多いです。
※ 三角比の発展内容として、ヘロンの公式という記事を投稿しています。
最後に、今回の記事と関連しそうな大学の数学の内容を述べておきます。
三平方の定理 :大学の数学への広がり
三平方の定理(ピタゴラスの定理)を用いて、座標平面や空間座標について、二点間距離が定義されます。
例えば、点 A(2, 3), B(5, 7) という座標平面上の二点について、線分 AB の長さを定義することができます。
(5, 3) という点を C とすると、座標平面上に三角形ABC があることになります。そこで、線分 AB の長さを点 A と点 B の距離とします。
三平方の定理より、
AB2 = AC2+CB2 です。
AC の長さは、5-2 より、3 です。
CB の長さは、7-3 より、4 です。
よって、
AB2 = 32+42 = 25 となります。
AB > 0 なので、AB は 25 の正の平方根となります。
(線分の長さなので、正の値となります。)
AB は、25 のルートなので、
AB = 5 です。
この二点間距離の定義は、座標空間についても、z 座標を加えて考えることで、同じように定義されます。
より一般的に、大学の数学では、n 次元ユークリッド空間について、二点間距離を定義します。n 個の成分について、距離を表す定義があります。
微分積分学など、大学で使う数学の基礎となる内容なので、距離関数という記事で、二点間距離について解説をしています。
また、代数学の基礎的な分野について、大学の数学で関連しそうな内容を述べておきます。
三平方の定理をはじめに証明するときに、直角三角形 4 個を貼り合わせて正方形を作りました。
そのときの 4 個の直角三角形の置き方ですが、回転移動という平面から平面への線形変換で回転させました。
一つの直角三角形ABC を中心角 90° で回転させます。さらに、90° 回転させて 3 個目の直角三角形の頂点の位置を作りました。
それから、もう一度 90° 回転させると、4 個目の直角三角形です。
さらに、もう一度回転をさせると、元の状態に戻ります。群論の内容で、位数 4 の元ということになります。
どれも合同な直角三角形なので、平行移動をさせて、「正方形WXYZ」を作りました。
この線形変換は、大学の数学で、線形代数学を学習するときに出てきます。
表現行列というブログ記事を以前に投稿し、そこで線形変換を行列で表すことを解説しています。
また、正方形に関連した線形代数学と群論の入門的な内容として、二面体群というブログ記事も投稿しています。
回転移動と鏡映変換という二つの線形変換によって生成される群の内容になっています。
※ reflectionという記事で、鏡映変換を行列で表し、sin、cos、tan、を使った数学2の内容と関連させて、具体的な状況を扱っています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。