球の表面積 | 積分を使って曲面の面積をどう定義するのか
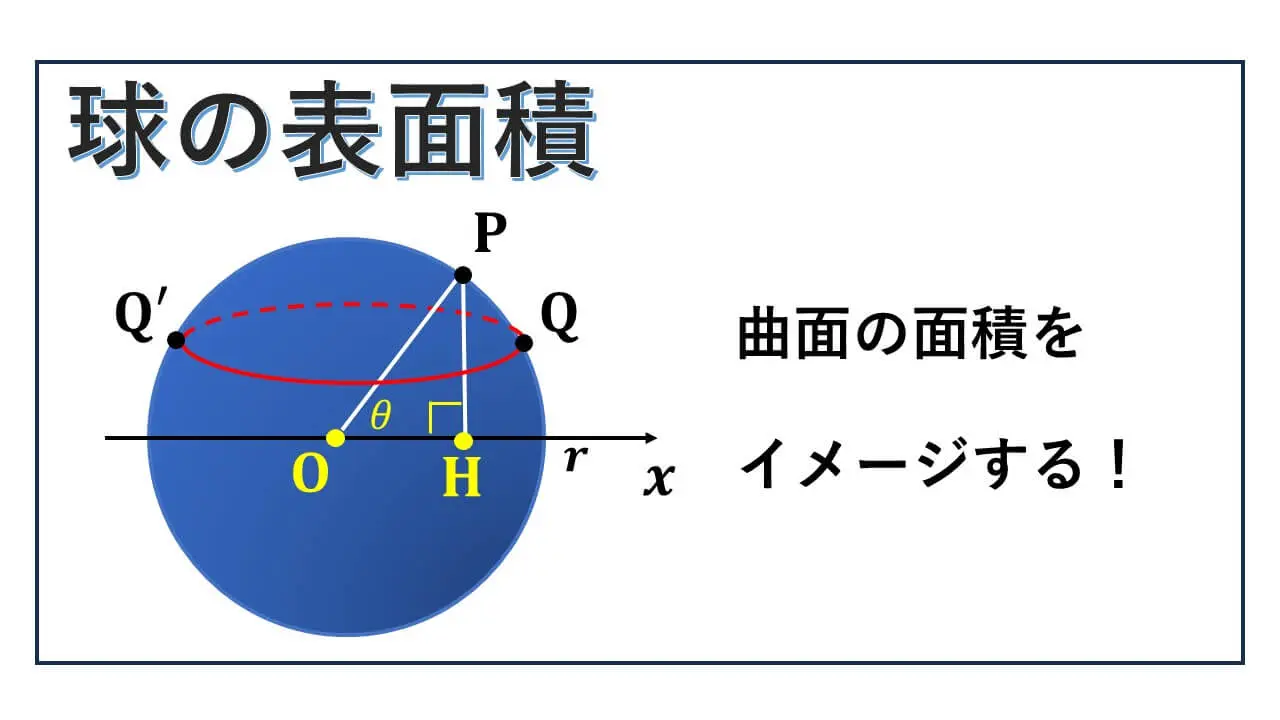
半径 r の " 球の表面積 “は、中学の数学で、その値が半径 r の円の面積の 4 倍となっているという事実として学習します。
その値にどうしてなるのかということは、大学数学の積分理論による必然的な帰結になります。
ただ、曲面の面積の定義までの厳密な一連の理論の証明は大変で長い道のりになります。
そこで、曲面の面積について、比較的に親しみやすい球の表面積で、抽象的な理論のソフトなイメージを持っておくために今回の記事を投稿しました。
「弧長という曲線の長さが絡む曲面の面積を、どうやって積分で定義するのか」ということに切り込むには、まずは親しみやすそうなイメージから。
それでは、高校の数学IIIから大学の積分理論へのつなぎ目になる部分について解説をします。
次の図では、空間座標の奥行きを表す軸は、計算で使わないので省略しています。
球の表面積 :弧に注目して曲面をつなぐ
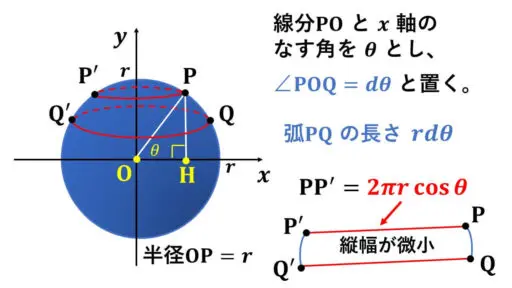
半径 r の球の表面上に点 P を取り、球の中心 O と結んだ線分(半径)と x 軸のなす角を θ ラジアンとします。
そして、点 P と x 軸との距離が PH の長さです。
この点 P と y 軸について対称な位置に点 P’ を取っておきます。
二点 P, P’ を通る平面で切ったときの断面積は、半径 が OH と同じ長さの円となっています。
この設定のもとで、なす角 θ のときに、点 P を xy-平面で切断した円の周上を微小に dθ ラジアンだけ動かして点 Q を考えます。
点 Q と y 軸について対称な点が Q’ です。
このように考えると、球に横線を赤色で描いたテープが巻き付いている状態になります。
図では見やすいように大き目に描いていますが、dθ が微小なので、弧PQ の長さは微小です。
厳密には、このテープの上の横線 PP’ の長さと下の横線 QQ’ は異なる長さですが、その差は微小なものになっています。
この θ を -π/2 から π/2 まで動かして、無数のテープを考え、無数のテープの面積の総和を球の表面積と思いたいわけです。
扇形POQ は、∠POQ = dθ を中心角で、半径が r です。
そのため、弧PQ の長さは、数学IIで学習した公式から、
rdθ となっています。
※ 弧度法という記事で、中心角 θ ラジアン、半径 r の扇形の弧の長さについて解説をしています。
また、三角比の定義から、
OH = 2πr・cos θ となっています。
大昔の近似の発想では、PP’Q’Q というテープの面積を、微小な長さなので弧がストレートだと思って、長方形として、面積を縦と横の長さの積と考えました。
厳密な理論を整備して、PP’Q’Q というテープのような曲面についての面積を定義しているのが大学の数学です。
ただ、理論の厳密な証明は、難しく長い道のりになるので、昔ながらのイメージが見える球の表面積を例として、曲面の面積について説明をします。
弧の長さと等しい線分へ跳躍する極限
弧PQ が rdθ で、PP’ = 2πr・cosθ という曲面の面積をどう定義するのかということが重要になります。
PP’ と QQ’ の長さも、微妙に異なるという状況です。
曲面の面積を定義するといっても、あまりに非現実的なものを定義してしまっては、実用的な応用を考えても使われるニーズがありません。
そこで、状況をよく整理してみます。
無数のテープを貼り合わせて球の表面積(側面積)と思いたいわけです。
これは、極限操作の出番です。
そこで、どうせ極限操作だったら、弧の長さ PP’ の線分を考えようというわけです。
縦 rdθ、横 2πr・cos θ の長方形を無数につなぎ合わせたものの面積も、限りなく近い面積。
それなら、微小な長方形を無数につなぎ合わせて、面積の総和とする積分を利用しようと思うわけです。
数学IIIの区分求積法で使ったような無数に小さい長方形の総和が積分の値で、その積分の値を面積とするというような発想です。
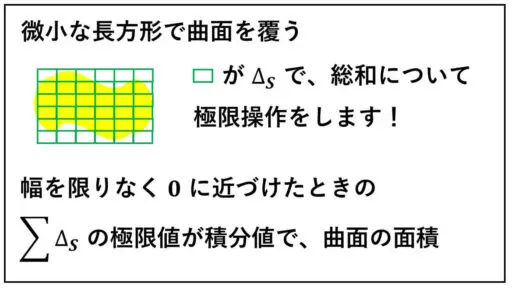
球の表面積の公式を中学の数学で学習しますが、厳密な証明は大学の数学になっています。
微小な長方形の面積の総和という極限操作による跳躍があるわけです。
曲面の面積を、微小な長方形をつなぎ合わせたものとして、積分を計算して、積分値を曲面の面積とするという発想を利用したのが、円の表面積です。
このような論理的な跳躍を支えるための厳密な理論が数学科の内容ということになります。
大学の数学科の2年生くらいになると、微分積分学が広がって、解析学になり、ベクトル関数を積分するということのレポート課題などで、球の表面積を計算するということも考えられます。
ただ、いきなり空間ベクトルを定義域とする関数を積分といったことを考えると、理論をしっかりと整備しておかなければなりません。
そこで、今回は、高校の数学III で学習をした積分の公式を使う計算で、球の表面積を求めます。
球の表面積 :数IIIの積分で計算
半径 r の表面積を S とします。
OP と x 軸のなす角が θ ラジアンのときに、微小な角度 dθ を使って考えたテープの曲面について微小な面積 ΔS の長方形を考えます。
縦 r・dθ、横 2πr・cos θ の長方形の面積が ΔS です。
ΔS = r・dθ・2πr・cos θ
= (2πr2cos θ)dθ です。
θ を -π/2 から π/2 まで動かして積分を計算します。
cos θ の定積分で、偶関数だから 0 から π/2 の積分の値の 2 倍となるという定積分で、よく使う計算をします。
球の表面積 S は次のようになります。
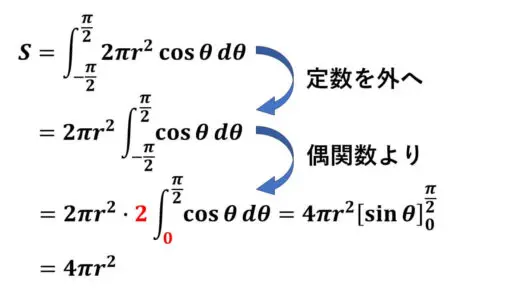
これで、4πr2 という見慣れた表面積の値となりました。
直径は半径の 2 倍で、偶関数の定積分を計算したときにも 2 倍となり、結果として 4 倍が出てきます。
コサインの定積分の値が 1 で、円の面積 πr2 は外に出ていたので、整理すると、円の面積を 4 倍した値になっています。
曲面の面積を定義するということを厳密に述べると、大学の解析学の内容になりますが、昔ながらの発想に触れつつ微小な長方形のイメージに触れられるので、球の表面積は良い経験になるかと思います。
より一般的に、a ≦ x ≦ b の範囲で曲線を回転させた回転体の表面積(側面積)についての式もありますが、球の表面積のときと同じ発想になります。
2π∫a y(1+(dy/dx)2)1/2 dx という回転体の表面積についての式は、扇形の弧の長さを縦の長さとした微小な長方形の総和の考え方です。
微小な弧の長さを縦の長さにして、微小な長方形を作って積分で曲面の面積を定義するという内容は、物理などの内容などで利用されたりします。
そんな内容の厳密な理論の下支えとして解析学の理論が使われています。
具体的な数字で表面積の計算
【例】
半径 5 の球の表面積
中学の数学で学習するときに出てきそうな内容です。
半径 r の球の表面積 4πr2 について、半径 r が 5 のときです。
そのため、
4π × 52 = 100π が、半径 5 の球の表面積となります。
この球の表面積を支えているのが、曲面の面積です。
数学科の解析学で、ベクトルの外積などを絡めて理論を学習したりします。
理論と理論を使う実践ということで、今回の記事では高校の数学IIIとのつなぎになるような部分のイメージについて述べました。
ちなみに、cos の定積分を計算しましたが、
三角関数の微分を学習してから、微分積分学の基本定理で三角関数の不定積分を数学IIIで学習します。
リンク先の記事で、微分の定義から三角関数の導関数についての公式を解説しています。
また、部分積分といった積分の内容も投稿しています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。