円の接線の方程式 | 中心(a,b)の円の接線をベクトルを使って求めます【数Cと数２の内容】

2023年7月22日

" 円の接線の方程式 “を求めるときに、円の中心が原点ではないときに、少し工夫が必要になります。

数学２の内容だと、点と直線の距離を考えるという求め方がありますが、計算が大変なときが多い気がします。数Cのベクトルを使うと、スムーズに公式が導けます。

一つの点を基準とした位置ベクトル表示と、座標を用いた成分表示で、内積を使って円の接線の方程式を求めます。

二つのベクトルが垂直に交わっているときに、内積の値が 0 になっていることを利用して、円の接線の方程式を求めます。

数Cの平面ベクトルの基礎的な内容を着実に使いこなすことが大切になります。

※ 後半では、数IIIの微分を使って接線の方程式を求めることについて解説をしています。

円の中心が、図のように原点とは限らないときでも、平行移動を使わずに接線の方程式をベクトルを用いて求めることを目指します。

円の接線の方程式 :位置ベクトルの基準

xy-座標平面上の点 A(a, b) は、原点 O(0, 0) を基準とすると、
ベクトル OA は、(a, b) です。

位置ベクトルの基準が原点 O のときは、点 A を表す位置ベクトルの成分表示は、座標そのものなので、楽です。

しかし、S(s, t), T(u, v) という異なる２点について、点 S を位置ベクトルの基準としたときに、点 T の位置ベクトルを成分表示させるときには、注意が必要です。

t→ と位置ベクトルを小文字の上に矢印をつけて表しますが、
t→ = (u－s, v－t) となります。

ST→ = OT→－OS→ が t→ のことなので、
OS→ = (s, t), OT→ = (u, v) について、
OT→－OS→ を計算したものが、位置ベクトル t→ についての成分表示となります。

位置ベクトルを考えるときは、どの点を基準に位置ベクトルを考えているのかということを意識することが大切になります。

今回の記事では、位置ベクトルの基準は、原点 O(0, 0) として、
s→ = (s, t), t→ = (u, v) と楽に表して計算を進めます。

このことに注意をして、点 (a, b) を中心とする円の接線の方程式を表す公式を求めます。

垂直に交わると内積の値が0

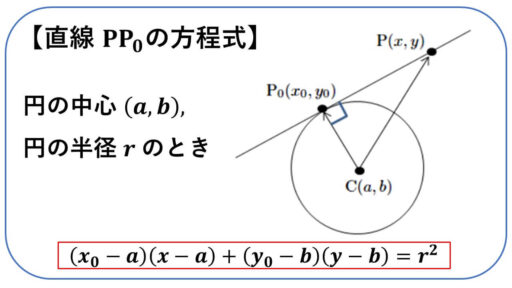
点 C(a, b) を中心とする半径 r の円について、円周上の点 P₀(x₀, y₀) における接線の方程式の公式です。

線分 CP₀ の長さが半径 r となっています。

このことをベクトルを使って表すと、ベクトルの大きさを表す絶対値の記号を使います。

|CP→₀| = r ということです。

直線 PP₀ が接線なので、
PP→₀ と CP→₀ が垂直に交わっています。

垂直に交わっているということは、平面ベクトルの内積の値が 0 となります。

ベクトルを使って内積を表すと、
PP→₀・CP→₀ = 0 となります。

ここで、原点 O を基準とする位置ベクトル表示を考えます。

点 P(x, y) は、求める接線の上にある任意の点です。

点 P の位置ベクトルは、
p→ = (x, y) です。

点 P₀ (x₀, y₀) の位置ベクトルは、
p→₀ = (x₀, y₀),
点 C(a, b) の位置ベクトルは、
c→₀ = (a, b) です。

位置ベクトルの基準を原点 O(0, 0) に設定したので、点の記号を小文字にし、そのまま座標が位置ベクトルの成分表示になってくれました。

円の接線の方程式 :位置ベクトルで成分表示

PP→₀ と CP→₀ が垂直に交わっていたので、
PP→₀・CP→₀ = 0 です。

ここで、点 C を始点にすると、
P₀P→ = CP→－CP→₀ です。

大文字のベクトルを考えているときに、始点をそろえるということも一つの手です。

そのため、
0 = CP→₀・P₀P→
= CP→₀・(CP→－CP→₀) となります。

同じベクトルで内積を計算すると、その値は絶対値の二乗です。

そのため、
0 = CP→₀・CP→－CP→₀・CP→₀
= CP→₀・CP→－|CP→₀|

|CP→₀| = r が円の半径だったので、
0 = CP→₀・CP→－r²

移項すると、
r² = CP→₀・CP→ となります。

ここで、CP→₀と CP→ を原点 O を中心とする位置ベクトルで表示します。

r² = (p→₀－c→)・(p→－c→) …(1)

(x₀, y₀) = OP→₀ = p→₀,
(x, y) = OP→ = p→,
(a, b) = OC→ = c→ でした。

そのため、
p→₀－c→ = (x₀－a, y₀－b) … (2)
p→－c→ = (x－a, y－b) … (3)

(2), (3) を (1) に代入し、
成分表示された内積の計算をすると、
r² = (x₀－a)(x－a)+(y₀－b)(y－b)

すなわち、
(x₀－a)(x－a)+(y₀－b)(y－b) = r² となります。

まとめ

中心 C(a, b), 半径 r の円周上の点についての接線の方程式

定点 P₀(x₀, y₀) における接線の方程式は、
(x₀－a)(x－a)+(y₀－b)(y－b) = r² と定数 a, b, r を用いて表される。

接線上の点 P(x, y) は、接線の上を自由に動くので、x と y は変数です。

変数と定数を区別して押さえておくことも大切になります。

それでは、この円の接線の方程式の公式を、具体的な例で使ってみます。

円の接線の方程式 :具体例で実践

中心 C(2, 3), 半径 5 の円が与えられたとします。

点 (5, 7) における接線の方程式を求めます。

(x－2)²+(y－3)² = 25 が、与えられた円を表す方程式です。

(5－2)²+(7－3)² = 9+16 = 25 なので、
点 (5, 7) は円周上の点です。

点 (2, 3), (5, 7) と半径である実数 5 は、与えられて定数です。

求める接線の上にある自由に動く点を (s, t) とします。

このとき、先ほどの接線の方程式の公式から、
(5－2)(s－2)+(7－3)(t－3) = 5² となります。

これを整理すると、変数 s と変数 t を使った一次の等式となります。

ちなみに、点 (s, t) が接点 (5, 7) に来たときのことを考えてみます。

s = 5, t = 7 なので、
(5－2)(5－2)+(7－3)(7－3) = 5² です。

これは、
(5－2)²+(7－3)² = 25 なので、
円の方程式に x = 5, y = 7 を代入した式と同じです。

少し話がそれましたが、s, t を用いた接線の方程式を整理しておきます。

5² = (5－2)(s－2)+(7－3)(t－3)
= 3(s－2)+4(t－3)
= 3s+4t－18 です。

移項して整理すると、
3s+4t = 43 となっています。

動き回る点を表す文字を,
s = x, t = y に置き替えると、
3x+4y = 43 という見慣れた直線を表す方程式になります。

直線上の点

接線の方程式を求めたときに、接点の x 座標と y 座標を代入して、左辺と右辺が一致しているのかを確かめておくと、計算ミスをしていたときに気がつくかもしれません。

3x+4y = 43 が接線の方程式で、
点 (5, 7) が接点の座標でした。

接点は、接線の上にある点で、円との唯一の共有点です。

x = 5, y = 7 を左辺に代入してみます。

3×5+4×7 = 15+28 = 43 です。

確かに右辺の 43 と一致しています。

図形を表す方程式は、いろいろですが、具体的な点の座標を代入したときに、両辺の値が一致していると、その点は図形上の点ということになります。

数Cで二次曲線を表す方程式が出てきたときも、その点が楕円などの上の点かどうかを確認するときに基本となる考え方です。

もう一つ具体的な内容で練習をします。

円の接線の方程式 :外部の点から引いた接線

【練習問題】

(x－5)²+(y－3)² = 4 は中心 (5, 3), 半径 2 の円の方程式です。

点 (3, 1) を通り、この円に接する接線の方程式を求めてください。

(3－5)²+(1－3)² = 8 ≠ 4 であり、
点 (3, 1) は、円の周上の点でないことが分かります。

点 (3, 1) と円の中心 (5, 3) との距離は、
{(5－3)²+(3－1)²}^1/2
= 8^1/2 > 4^1/2 = 2 です。

つまり、二点間の距離が、半径よりも大きいので、点 (3, 1) は円の外部の点だと分かります。

中学の数学で直角三角形の合同の内容で、二本の接線が引けるということを押さえた上で、論理的にミスなく日本の接線の方程式を求めることが大切になります。

点 (3, 1) を通り、この円に接する接線の接点を、点 (a, b) とします。

(a, b) が接点の座標なので、接線の公式から、
(a－5)(x－5)+(b－3)(y－3) = 4 … ■

これが、求める円の接線の方程式です。

y を x の式で表したいところですが、計算が大変です。合成関数の微分の公式を使って、両辺を x で微分すると、接線の傾きが得られます。

直線について、平均変化率（変化の割合）は常に一定で、直線の傾きと一致します。

そのため、dy/dx が定数で、接線の傾きと一致します。

直線の傾きを求めるためには、y を x の一次式の形で表す必要があるので、その計算を微分を使って計算します。

(a－5)×d/dx(x－5)+(b－3)d/dx(y－3) = 0 です。

合成関数の微分の公式より、
d/dx(y－3) = (y)’×dy/dx + d/dx(－3)
= dy/dx です。

よって、
(a－5)+(b－3)dy/dx = 0 となります。

ここで、b = 3 の場合と、b ≠ 3 の場合が考えられます。

b = 3 とすると、
(b－3)dy/dx = 0 となるので、
a = 5 となります。

これは、点 (5, 3) と接点 (a, b) が一致することになります。

点 (5, 3) は円の中心だったので、矛盾が生じました。

そのため、背理法から、
b ≠ 3 でなければなりません。

そのため、b－3 ≠ 0 です。

0 でない実数で割ることができるので、
dy/dx = －(a－5)÷(b－3) … ★

定数 a と b を使って、円の接線の傾きを表すことができました。

場合分けをして求める

円の外部から円へ接線が二本引けることは、中学の数学から知っている知識です。場合分けを考えると、二本の接線の方程式が得られます。

接点 (a, b) は円周上の点なので、
(a－5)²+(b－3)² = 4

ここで、a－5 = 0 の場合と a－5 ≠ 0 の場合が考えられます。

【a－5 = 0 の場合】

a = 5 のとき、接点 (5, b) は円周上の点だから、
(5－5)²+(b－3)² = 4 です。

よって、b－3 = 2 または b－3 = －2 となります。

つまり、b = 5 または b = 1 です。

b = 5 と仮定すると、
(5, 5) が円の接点となります。

★より、
dy/dx = －(5－5)÷(5－3) = 0

接線の傾きが 0 で、接線が点 (3, 1) を通るので、
y = 1 が接線の方程式となります。

しかし、y = 1 は接点のはずの (5, 5) を通らないため矛盾です。

よって、背理法から、b ≠ 5 でなければなりません。

そのため、b = 1 の方のみを考えることになります。

今、(5, 1) が接点の座標です。

★より、
dy/dx = －(5－5)÷(1－3) = 0 が接線の傾きです。

直線の傾きである変化の割合が 0 なので、接線は横軸である x 軸に平行となっています。

点 (3, 1) を通る接線なので、
y = 1 が求める接線の方程式となります。

【a－5 ≠ 0 の場合】

今、接点は円周上の点だから、
(a－5)²+(b－3)² = 4 です。

ここで、c = a－5 ≠ 0 と置くと、
c²+(b－3)² = 4 … (1)

接線は (3, 1) を通るので、★より、
(a－5)(3－5)+(b－3)(1－3) = 4

つまり、－2a+10－2b+6 = 4 となり、
b = －a+6 … (2)

c = a－5 より、a = c+5 だから、
b = －(c+5)+6 となります。

すなわち、b = －c+1 … (3)

(3) を (1) に代入すると、
c²+(－c+1－3)² = 4 となります。

(－c+1－3)² = {(－1)(c+2)}²
= (－1)²(c+2)² = (c+2)² と変形します。

すると、
c²+(c+2)² = 4 と c についての二次方程式が得られました。

よって、2c²+4c+4 = 4 なので、
2c(c+2) = 0 です。

c ≠ 0 だったので、c+2 = 0 となり、
c = －2 です。

これを (3) に代入すると、
b = －(－2)+1 = 3

b = 3 を (2) に代入すると、
3 = －a+6 となります。

これで、a = 3 です。

以上から、接点 (a, b) = (3, 3) です。

■より、接線の方程式は、
(3－5)(x－5)+(3－3)(y－3) = 4 です。

つまり、－2(x－5) = 4 となり、
x = 3 が求める接線の方程式となります。

これで、接線の方程式が全て求まりました。

a = 5 の場合は、接点が (5, 1) で、
y = 1 が接線の方程式です。

a ≠ 5 の場合は、接点が (3, 3) で、
x = 3 が接線の方程式です。

どちらも確かに点 (3, 1) を通っています。

実は、円外の点 (3, 1) を原点 (0, 0) に来るように x 軸方向へ －3, y 軸方向へ －1 だけ平行移動をして図を描くと、すぐに接線の方程式が分かります。

しかし、敢えて図を描かずに、論理だけで考察を進めてみると、上で述べたように図形と方程式や二次曲線と数３を融合させた内容の良い練習となります。

ここからは、数IIの接線の内容を復習しつつ、e を底とする指数関数の接線について解説をします。

接線の傾き :微分の利用

【数２の公式】

傾き m で、点 (a, b) を通る直線の方程式は、
y － b = m(x － a) である。

接線も直線なので、この公式を使うことが多いです。

ただ、この公式ですが、符号がマイナスになっていたり、切片を求めるときに移項をしたりするため、覚えにくい形です。

そこで、忘れたときのために、自分で導けるように理解をしておくと良いかと思います。

まず、この直線の方程式についての公式を導きます。

傾きが m で、点 (a, b) を通る直線の方程式を、
y = mx + d … (1) と置きます。

d が直線の切片の値です。

この直線 (1) の上に、点 (a, b) があるので、
x = a, y = b を代入します。

すると、b = ma + d … (2) となります。

(1) － (2) より、
y － b = m(x － a) となります。

これで、直線の方程式が導けました。

ちなみに、分配法則で括弧を外し、b を右辺へ移項すると、切片の値が分かります。

y = mx －am + b なので、
d = －am + b が切片の値です。

まず、y － b = m(x － a) という形を導き、切片の値を知りたいときには、計算して整理をします。

では、この公式を使いつつ、接線の方程式を具体例を用いて求める練習をします。

数IIIの典型例

e をネイピア数とし、e を底とする指数関数のグラフについて、接線の方程式を考えます。

※ ネイピア数という記事で e の定義について解説しています。

y = f(x) = e^x の点 (0, 1) における接線の方程式を求めます。

e⁰ = 1 なので、f(0) = 1 です。

つまり、点 (0, f(0) = (0, 1) は、
y = f(x) = e^x 上の点です。

数３の微分ですが、e^x を x で微分しても e^x のままです。

そのため、f'(x) = e^x なので、
f'(0) = e⁰ = 1 です。

これで、接線の傾きが 1 と分かりました。

点 (0, 1) を通る直線なので、数２の公式を使うと、接線の方程式が得られます。

つまり、y － 1 = 1 × (x － 0) が求める接線の方程式です。

整理すると、y = x + 1 となります。

ゆえに、y = x + 1 が、
点 (0, 1) における y = e^x の接線の方程式です。

単元を学習し始めるときに、グラフを用いた図は理解の助けになります。しかし、難しい問題だと、グラフの概形をはっきりと認識できない状態で推論を進めるときもあります。

この記事では、敢えてグラフを描かずに、論理的な推論を進めます。

今、y = x + 1 が点 (0, 1) における接線の方程式と述べましたが、本当に 1 点のみを共有しているのかを確かめてみます。

微分法の応用

★ f'(x) < 0 となっている区間において、y = f(x) は単調減少関数です。

★ f'(x) > 0 となっている区間において、y = f(x) は単調増加関数です。

この増減表に関わる内容を使って、
y = x + 1 と y = f(x) = e^x が点 (0, 1) の 1 点のみでしか交わっていないことを確かめます。

g(x) = e^x － (x + 1) と置きます。

g'(x) = e^x － 1 です。

x < 0 のとき、e^x < 1 で、
x = 0 のとき、e⁰ = 1 で、
x > 0 のとき、e^x > 1 です。

そのため、x < 0 の範囲で、y = g(x) のグラフは単調減少で、x = 0 で最小値（極小値）を取っていると分かります。
（x > 0 の範囲で、y = g(x) は単調増加しています。）

よって、どんな実数 x に対しても、
g(x) = e^x － (x + 1) ≧ 0 となっていることが分かりました。

x を左から 0 に近づけていくと、段々と g(x) の値が減少していき、x が 0 となったとき、g(0) の値が 0 です。

そして、x を 0 から右へと遠ざけていくと、g(x) の値は増加していきます。

このため、g(0) = 0 が y = g(x) の最小値（極小値）です。

すなわち、g(x) = 0 となるのは、x = 0 のときに限ります。

得られた内容を不等式と方程式を使ってまとめます。

重要なまとめ

どの実数 x に対しても、g(x) ≧ 0 ということを不等式の形で述べると、
e^x － (x + 1) ≧ 0 です。

不等式の同値変形より、
e^x ≧ x + 1 と同値です。

e^x － (x + 1) = 0 は、
e^x = x + 1 と同値です。

曲線のグラフと微分を用いた増減表の考え方は、不等式や方程式を用いて表されるときもあります。

内容をまとめます。

【まとめ】

実数 x に対して、e^x ≧ x + 1 が成立する。

等号成立は、x = 0 のときに限る。

微分と単調性についての増減表の考え方は、不等式への応用としても出題されるときがあります。論理を用いての同値変形が重要になります。

中には、逆が成立しないというようなときもあるので、正確な論理の運用が大切になる内容になります。

今回は、y = e^x について、x = 0 における接線が、
y = x + 1 ということを導きました。

この内容は、微積の分野で使われることがあるので、事実として押さえておくと良いかと思います。

今回、導いた不等式を利用することで、
相加相乗平均についての定理を証明することができます。

この記事では、数Cのベクトルを用いた円の接線の方程式の求め方でしたが、数３の合成関数の考え方で接線の方程式を求めることもできます。

二次曲線という記事で、微分を用いた接線の求め方について解説をしています。

また、直線のベクトル方程式について、平行や垂直についての理論があります。

方向ベクトル-法線ベクトルという記事で、今回の記事で扱った内容に関連する内容として平行や垂直についての条件を満たす直線の方程式の求め方について解説をしています。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。