累乗根 | 正数aに対してn乗してaになる正の実数は、ただ1つのみ

" 累乗根 “について、複素数平面における図をイメージしながら解説をしています。
正の実数 a が与えられたとき、n 乗すると a となる複素数は n 個存在します。
このことを一般の自然数 n に対して証明します。
式だけ見ていると難しそうですが、図形的なイメージをすると、スムーズに理解ができるかと思います。
zn = a という z についての方程式に関する累乗根の内容を解説します。
arg z を、複素数平面において、複素数 z に対して z と横軸とのなす角である偏角とします。
時折、この記号を使っています。
図形的なイメージでアプローチしやすいように、具体例から説明します。
a = 1, n = 3 という設定で、
z3 = 1 を満たす複素数 z をすべて求めます。
累乗根 :具体例で様子を見る
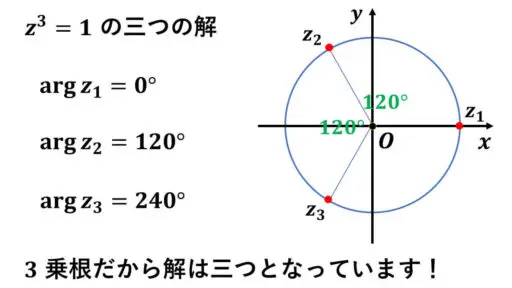
横軸が実軸、縦軸が虚軸という複素数平面において、イメージをもつと、一般の累乗根について理解しやすくなります。
z3 = 1 を満たす複素数 z の値ですが、1 つはすぐに見つかります。
1 は 3 乗しても、その値は 1 のままなので、1 という実数が解(根)となっています。
cos 0°+ i sin 0° = 1 なので、
z1 = 1 の偏角は 0° です。
次に、ド・モアブルの定理を使うと、残りの二つの解も得られます。
cos 120°+ i sin 120° を z2 と置きます。
プログラミング風に述べると、
z2 := cos 120°+ i sin 120° です。
英語で述べると、
We put z2 cos 120°+ i sin 120° という第4文型の形です。
この z2 の 3 乗を、ド・モアブルの定理を用いて計算してみます。
(cos 120°+ i sin 120°)3
= cos 360°+ i sin 360°
= 1 + i × 0 = 1 です。
確かに z2 を 3 乗すると、1 になっています。
角度が3倍されて 360°という特徴的な角の大きさとなることから、明確に計算ができました。
上の図を見ると、z1 を原点 O を中心として左回りに 120°だけ回転させた位置にあるのが z2 です。
なんで 120°かというと、3乗根なので、360°を3等分したからです。
z2 から、さらに 120°左回りに回転させた位置にある点に対応する複素数を z3 と置きます。
つまり、cos 240°+ i sin 240°を z3 と置きました。
3 乗を計算してみます。
(cos 240°+ i sin 240°)3
= cos 720°+ i sin 720°
= 1 + i × 0 = 1 となります。
z3 も 3 乗すると 1 となることを確認できました。
一般に n 次の複素係数の方程式は、重解を含めて n 個の解をもつというのが代数学の基本定理です。
この厳密証明は大学の数学の内容となります。
この記事では、n 乗根をこの基本定理を意識することなく複素数平面のイメージから n 個の累乗根の存在を確かめるように議論を進めています。
角の等分を明確に
cos θ + i sin θ の値は、θ が 360°の整数倍となっているときに、1 となります。
360°をラジアン単位で表し、文字式で角の大きさについて見てみます。
弧度法については、リンク先の記事で数IIの範囲で解説をしています。
360° は 2π ラジアンです。
z1 = cos 0+ i sin 0 から始めて、左回りに複素数平面において解となる複素数を順に考えました。
2π を n 等分した角の大きさを 1 つずつ考えます。
arg z2 = 2π × 1/3,
arg z3 = 2π × 2/3 で、残りの2個の解が得られました。
z2 や z3 は、3 乗すると、ド・モアブルの定理から、角の大きさが 2π の整数倍となることが分かります。
そのため、z3 = 1 に代入すると、左辺と右辺の値が一致して解となるわけです。
この内容を、一般の n へと拡張することができます。
しかも、正の実数 a に対して、
zn = a の解である a の n 乗根の内容へと結びつけます。
角の大きさについては、文字式の計算で 2π の整数倍となることが分かるのですが、1 を a にしたときに、始めの一歩に議論のギャップが生じています。
その溝を埋めるのが、実数の範囲での連続関数の連続性です。
累乗根 :正の実数根の存在
正の実数 a と、2 以上の自然数 n が与えられたとします。
このとき、
zn = a を満たす複素数 z の存在を示すところから議論をスタートします。
n = 1 のときは、実数 a 自身が唯一の解という自明な状況なので、n を 2 以上としています。
まずは、実数解が、必ず存在するということを示します。
そこで、f(x) = xn とし、
y = f(x) という n 次の多項式関数のグラフの概形を考えます。
この x の定義域は実数全体とします。
ここで、増減表の発想が大切になります。
f'(x) = nxn-1 です。
そのため、x > 0 の範囲では、
f'(x) > 0 となっています。
これは、y = f(x) のグラフが、x > 0 の範囲で、単調増加していることを示しています。
ここで、y = f(x) の定義域を x > 0 の範囲に制限して正確に考察を進めます。
x > 0 の範囲において、単調に +∞(無限) へと向かって上昇し続ける 1 本の曲線です。
一方、正の実数 a について、
y = a のグラフは、横軸に平行な直線となっています。(a は定数という扱いです。)
よって、x > 0 の範囲において、
y = f(x) という右上がりの 1 本の曲線と y = x のグラフが、ただ 1 つの点で交わることになります。
この唯一の交点の x 座標の値を a1/n と表すことにします。
数学IIで学習する a の n 乗根です。
f(a1/n) = (a1/n)n = a となっていることが、グラフの情報から分かりました。
そのため、zn = a を満たす複素数 z として、実数解が一つ見つかりました。
さらに、数学Cの複素数平面における考察を加え、残りの解を導きます。
z1 = a1/n と置き、残りの (n-1) 個の複素数解を求めます。
n = 2 のときは、中学の数学から、よく知っている内容となります。
z2 = a を満たす正の実数解は、
z1 = a1/2 です。
分数の指数を使っていますが、ルート a ということです。
この符号をマイナスにしたものも解となります。
(-a1/2)2 = (-1)2(a1/2)2
= a です。
a が正の実数なので、二乗をすると、そのままルートが外れて a となるということに注意すると、絶対値の記号が出てこないことが分かります。
このため、z2 = -a1/2 も、
z2 = a の解です。
これで、n = 2 のときの解を全て求めました。
n = 2 のとき、正の実数解は、ただ1つとなっています。
n個の複素数解
ここからは、n ≧ 3 として、n 乗根を全て求めます。
z1 = a1/n という正の実数解が一つ見つかっているという状況でした。
残りの (n-1) 個の解を求めます。
z2 の偏角は、
2π ÷ n = 2π/n とします。
z2 から 2π/n ずつ偏角の大きさを大きくします。
z2 = cos 2π/n + i sin 2π/n,
z3 = cos 2π・2/n + i sin 2π・2/n,
・・・
zk の偏角を k を用いて表します。
cos 2π(k-1)/n + i sin 2π(k-1)/n とします。
zk の k より一つ小さい (k-1) を偏角に掛けるという規則です。
k を 2 から n まで走らせます。
z1, z2, z3, … , zn-1, zn という n 個が、解となります。
cos 2π(n-1)/n + i sin 2π(n-1)/n という zn が左回りに見たときの最後の解となっています。
もう一度 2π/n だけ移動させると、2π となり、円周上を一周して z1 の位置に戻るというわけです。
zk を n 乗は、ド・モアブルの定理で計算できます。
arg zk は、2π(k-1)/n の n 倍となります。
つまり、
arg zk = 2π(k-1) です。
これは 2π の整数倍なので、
cos 2π(k-1) = 1,
sin 2π(k-1) = 0 となっています。
そのため、
2 ≦ k ≦ n について、
(zk)n = 1 + i × 0 = 1 です。
これで、zn = a の n 個の解が全て得られました。
z1, z2, z3, … , zn-1, zn は、偏角が、どの二つも異なっているので、円周上の異なる点に対応する複素数となっています。
では、zn = a の n 個の解が得られましたが、正の実数となっているものが何個あるのかを観察してみます。
累乗根 :正の実数解はただ一つ
今、n ≧ 3 の場合について議論をしていました。
半径 a の円周上の点で、横軸である実軸との交点は、二つだけです。
そのときの偏角は、0 と π の二つだけです。
z1 の偏角が 0 となっていて、これが1つの実数解となっています。
z2, z3, … , zn-1, zn の中に、正の実数解が存在しないことを確認します。
k を 2 以上 n 以下の自然数とし、zk が正の実数だと仮定し、矛盾を導きます。
まず、2π(k-1)/n = 0 の場合を考えます。
2π(k-1) = 0 となり、
k = 1 となってしまいます。
これは、k ≧ 2 であることに反します。
そこで、偏角について、もう一つの可能性を考えます。
つまり、
2π(k-1)/n = π となっている場合を考えます。
すると、この k について、偏角が π ラジアン(180°) です。
これは、zk の位置は、z1 と縦軸について対称な位置となっています。
そのため、
zk = -z1 = -a1/n です。
a1/n は正の実数なので、-a1/n は負の実数となっています。
そのため、zk は負の実数解ということになります。
これは、zk が正の実数解であったことに矛盾しています。
以上より、背理法から、
z2, z3, … , zn-1, zn の中に、正の実数解が存在しないことを示せました。
n が偶数のときに、負の実数が入り込むこともありますが、正の実数根は z1 のみです。
関連する記事について
この記事では、実数と複素数という数学の用語を使いました。
虚数と複素数の違いという記事で、実数・虚数・複素数の定義を正確に説明しています。
正の実数 a が与えられたとき、
zn = a の解となる n 乗根ですが、大学の数学科の数学にもつながります。
累乗根の内容を初等整数論もしくは環論で利用する内容として、オイラーのファイ関数の理論があります。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。