ド・モアブルの定理 | マイナス乗のときにも落ち着いて証明【回転角と大きさを意識】

2023年3月21日

" ド・モアブルの定理 " を証明するときに、回転角と大きさを意識することで、極形式の計算に慣れることができます。

複素数の乗法と回転運動を結びつけながら計算をすると、見通しも立てやすいかと思います。

この記事の証明では、帰納法を使うことなく、図形的なイメージから必然的に結果を導きます。

サムネイルの図の内容が、ド・モアブルの定理を証明するときの本質部分になります。

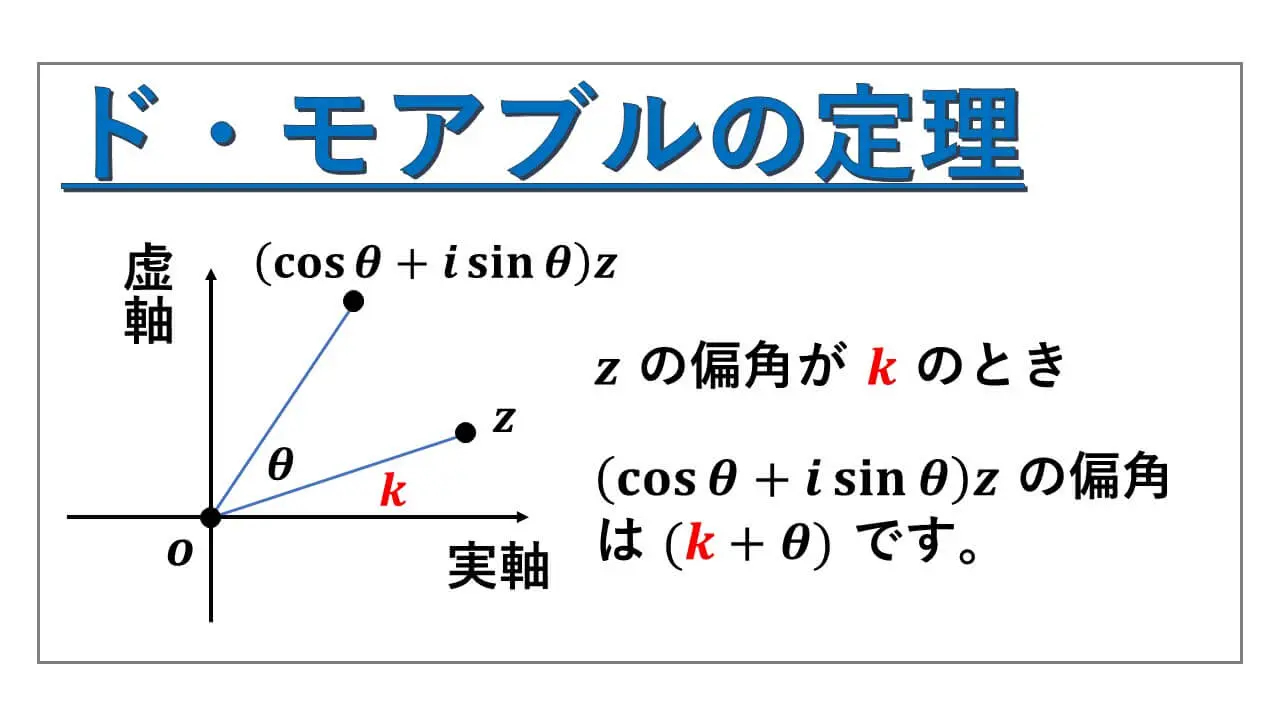
cos θ + i sin θ を複素数 z に掛けると、z の大きさである絶対値はそのままで、偏角だけが変化します。図形的には、原点を中心に、左回りに θ だけ角度が動くことになります。

ド・モアブルの定理の証明では、マイナスの指数のときを場合分けで処理して、自然数のときの議論を利用します。

複素数の乗法と回転について説明をしてから、定理の証明へと向かいます。

ド・モアブルの定理 :証明のための準備

【命題】
複素数 z の偏角が k で大きさを r とする。
つまり、z = r(cos k + i sin k) とする。

このとき、実数 θ について、
(cos θ + i sin θ)z =
r{cos (θ+k) + i sin(θ+k)}

(cos θ + i sin θ) を z に掛けると、大きさの r はそのままで、偏角が θ だけ動きます。

複素数平面において、原点を中心とする左回りの θ 回転をイメージすることで、計算を行いやすくなります。

この命題を証明するにあたって、次の定理を使います。

【加法定理】

sin(x+y) = sin x cos x+cos x sin y
cos(x+y) = cos x cos y－sin x sin y

加法定理より

※ リンク先の記事では、大学の複素三角関数の加法定理として解説をしています。

角の範囲を実数に限定して使用すれば、数学２の加法定理の通りです。

では、命題を証明します。

回転運動の命題の証明

(cos θ + i sin θ)z は、
r(cos θ + i sin θ)(cos k + i sin k) です。

そのため、|z| = r は放っておいて、三角関数の部分の乗法を計算します。

(cos θ + i sin θ)(cos k + i sin k) を展開をして、実部と虚部に分けます。

実部「cos θ cos k – sin θ sin k」、
虚部「 i(sin θ cos k + cos θ sin k」となっています。

ここで、実部と虚部のどちらにも加法定理を使います。

実部「cos (θ + k)」、
虚部「sin (θ + k)」となります。

よって、
(cos θ + i sin θ)(cos k + i sin k)
= cos (θ + k) + sin (θ + k)

両辺に r を掛ければ、
r(cos θ + i sin θ)z =
r(cos (θ + k) + sin (θ + k))【証明完了】

この命題が、ド・モアブルの定理を導きます。その前に、逆数について述べておきます。

cosθ+isinθの逆数

θを実数とすると、
cos θ + i sin θ ≠ 0 です。

理由は、原点を中心とする単位円周上の点に対応する複素数だからです。

ゼロでない複素数には、逆数が存在します。

逆数とは、その数と積をとると 1 になる数のことです。

(cos θ + i sin θ)(cos (－θ) + i sin (－θ)) は、θ から －θ だけ回転するので、大きさは 1 のままで、偏角が 0 となっています。

そのため、cos 0 + i sin 0 = 1 が、
(cos θ + i sin θ)(cos (－θ) + i sin (－θ)) の値です。

(cos (－θ) + i sin (－θ)) と積をとると、1 のなったので、逆数の定義から、
(cos θ + i sin θ)^-1
= cos (－θ) + i sin (－θ)

この －1 乗というのは、その複素数の逆数という意味です。

ここまでの内容を使って、ド・モアブルの定理を証明します。

ド・モアブルの定理 :定理の証明

【定理】
r と θ を実数とし、n を整数とする。

z = r(cos θ + i sin θ) という複素数に対して、
zⁿ = rⁿ(cos nθ + i sin nθ)

ただし、n が負の整数の場合を考えるときは、z ≠ 0 のときとする。

＜証明＞

(cos θ + i sin θ)(cos θ + i sin θ) に、先ほど示した【命題】を使います。

(cos θ + i sin θ)² =
(cos θ + i sin θ)(cos θ + i sin θ) です。

絶対値が 1 で、θ から θ 回転するので、偏角は 2θ です。

そのため、
(cos θ + i sin θ)² = cos 2θ + i sin 2θ

　
この指数乗を繰り返すと、2 以上の自然数 n に対して、
(cos θ + i sin θ)ⁿ は絶対値が 1 のままで、
θ から (n – 1)θ だけ偏角が動くので、
(cos θ + i sin θ)ⁿ =
cos nθ + i sin nθ … (★)

以上より、自然数 n に対して、指数法則より、
zⁿ = rⁿ(cos θ + i sin θ)ⁿ

さらに、★ より
zⁿ = rⁿ(cos nθ + i sin nθ)

これで、n が自然数のときに定理が成立していることを示せました。

n = 0 のときは、z⁰ = 1 です。

つまり、
cos (0×θ) + i sin (0×θ)
= cos 0 + i sin 0 = 1

よって、n = 0 のときにも成立しています。

残りは、n が負の整数のときです。

つまり、マイナス乗のときにも定理が成立していることを示します。

マイナス乗の場合

複素数の指数がマイナスのときは、その複素数を分母に置きます。ただし、複素数の負の整数乗はゼロでない複素数についての定義です。

そのため、定理のただし書きで、「負の整数乗を考えるときは、z が 0 でないとき」としています。

よって、ここからは、z が 0 でない場合について議論をします。証明は、次のようになります。

n を自然数とすると、

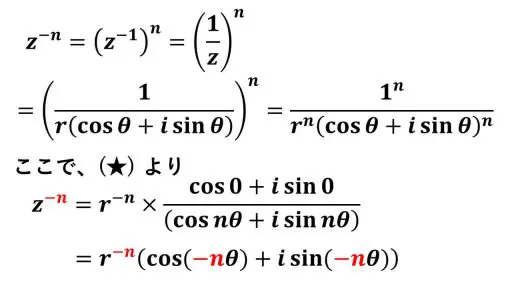
これで、定理の結論の n を －n にしたものになっているので、マイナス乗のときにも定理が成立しています。【証明完了】

ここで、補足です。

ゼロでない複素数 z と自然数 n について、
z^-n とは、z の逆数 z^-1 を n 個で積をとった値のことです。

例えば、n = 3 のときだと、z^-3 は、z^-1 を 3 個掛け合わせたものです。

そのため、
(z^-1)×(z^-1)×(z^-1)
= (z^-1)³ = z^-3

負の整数乗の計算は、定義に基づいて理解をしておくと良いかと思います。

ちなみに、先ほどの証明で、z ≠ 0 としたので、大きさ r は 0 ではありません。

大きさの r は実数なので、ゼロでない実数の逆数は、分母と分子を逆にした数です。

実数の指数法則は、
r^-n=(r^-1)ⁿ=(1/r)ⁿ でした。

先ほど述べた複素数の逆数については、複素数の除法という記事で詳しく解説をしています。

それでは、証明したド・モアブルの定理を使って、三倍角の公式を示します。

ド・モアブルの定理 :実際に使用

cos 3x = 4cos³x － 3cos x
sin 3x = －4sin³x + 3sin x

これらは、(cos x + i sin x)³ から得られます。

ド・モアブルの定理から、
(cos x + i sin x)³ =
cos 3x + i sin 3x … (1)

次に 3 乗を展開します。

(cos x + i sin x)³ =
cos³x + 3cos²x(i sin x) + 3cos x(i sin x)²
+ (i sin x)³
= cos³x + i(3cos²x sin x)
– 3cos x sin²x – i sin³x

よって、(cos x + i sin x)³ を実部と虚部に分けて整理します。

実部「cos³x – 3cos x sin²x」,
虚部「3cos²x sin x – sin³x」

(1) の実部、虚部とそれぞれ比較すると、
cos³x – 3cos x sin²x = cos 3x,
3cos²x sin x – sin³x = sin 3x

後は、sin²x + cos²x = 1 の関係を利用して変形をすると、三倍角の公式となります。

cos 3x と等しい式から変形します。

cos³x – 3cos x sin²x =
cos³x – 3cos x(1 – cos²x)
= 4cos³x－3cos x となります。

まず、cos 3x について示せました。

sin 3x と等しい式も、同じ要領で変形します。

3cos²x sin x – sin³x =
3(1 – sin²x)sin x – sin³x
= 3sin x－4sin³x です。

加法定理だけで三倍角の公式を示せるのですが、昔からド・モアブルの定理の練習問題などで出てくるので、示しておきました。

大学の内容について

自然数 n について、zⁿ = 1 を満たす複素数 z を 1 の n 乗根といいます。

そして、その数自身は 1 ではないのだけれども、n 乗したときに、はじめて 1 となる複素数のことを 1 の原始 n 乗根といいます。

複素数の n 乗ということで、z を極形式の形にして、ド・モアブルの定理を使うことを考えます。

大学の数学では、群や環という代数構造が扱われます。

複素数に関連した乗法群の内容として、トーラス（円環）という記事を投稿しています。

数学Cで、具体的な練習問題が出てくるかと思いますが、
円分多項式という大学の数学の内容にもつながります。

以前に投稿をしたリンク先のブログ記事では、大学の数学として、「円分多項式が必ず整数係数となっている」ことの証明を述べています。

この内容は、大学の代数学の分野の内容となります。

高校の数学に話を戻すと、数学Cや数学３で、三角関数の式の書き換えが大切になります。

今回の内容でも、加法定理が効いていました。

和積変換公式（積和変換も）という記事で、三角関数の変形を解説しています。
宜しければ、ご覧ください。

数学３Cの学習は、数学２Bなどの他の単元との融合もあるので、大変かと思いますが、できそうなところから基礎を押さえることが大切かと思います。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。