命題 – 仮定 – 結論 | 否定や逆に対偶を使いこなせるようになるために!

高校数学を学習するときに、「 命題 – 仮定 – 結論 」 に使われている変数(文字)の範囲となる集合を認識することが必要になります。
命題の構成を正しく認識できると、背理法や対偶といった間接証明を正しく実行できるようになります。
そのため、命題 (proposition) の構成を押さえておくと、問題を解くための解決策が増加します。
すなわち、背理法や対偶を正しく使えるようになると、その分だけ問題を解くためのアプローチが増えます。
数学の論理を押さえ、様々な論法を使いこなすことで、問題を楽に解けるアプローチを見つけられるときもあります。
命題 – 仮定 – 結論 :命題の構成を把握
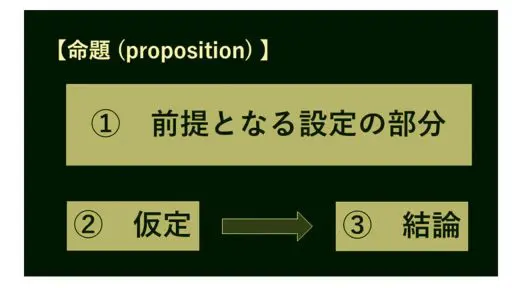
命題は、①前提となる設定、②仮定、そして③結論という3つの部分からできています。
背理法や対偶命題を考えるときに、①の扱いをどうするのかということを認識しておかないと、有効な間接証明が、肝心のときに使えないということになってしまいます。
簡単な説明ですぐに認識できるので、数学の学習をするときには、早い段階から押さえておくと、良い基礎となります。
高校数学を学習するときに、盲点となりやすいのが、「②仮定」の前に「①前提となる設定」があるということです。
命題は、「正しいか、正しくないか」のどちらか一方のみで、数学のルールに基づいて真偽が確定できるものですが、命題が上に書いている 3 部構成になっていることを知っておく必要があります。
命題を見たときに、①と②と③の部分を正しく認識できないと、背理法や対偶を考えることができなくなってしまいます。
前提と仮定の区別
特に注意点は、「①前提となる設定」と「②仮定」の区別が正しくできるかどうかです。
この区別をするために、次のことを知っておくと、①と②の区別がつきやすくなります。
数学では、文字を書いたときに、必ずその文字に代入できる値の範囲を表す集合を意識しなければならない。
この内容を押さえておくと、「①前提となる設定」と「②仮定」の部分を正しく区別しやすくなります。
では、次は、対偶命題の構成についてです。
命題 – 仮定 – 結論 :命題の対偶
高校数学を学習し始めたときに、対偶を考えるときに、「仮定と結論を逆にして、それぞれを否定する」というように学習します。
この内容自体は正しい内容になり、命題の対偶を考えるときに、実行する過程です。
ただし、これだけでは、「①前提となる設定」の部分をどうするのかということについて述べられていません。
このブログのメインの部分を先に書きますと、対偶を考えたり、背理法で証明をするときに、「①前提となる設定」は、はじめにある命題のままにしておき、一切の変更をしません。
この数学のルールを知らないと、背理法や対偶が正しく使えないということになってしまいます。
ただ、はじめの設定のまま変更しないという単純なことを知っておくだけで、命題の対偶を証明するというようなときに、命題をどのように変更すれば良いかということが分かります。
では、具体的な問題で、「対偶をとる」ということを実践してみます。
命題の対偶をとる詳細
x を整数とする。(① 前提となる設定)
このとき、x が 3 の倍数 ならば、
2x は 6 の倍数となる。
この命題の①前提となる設定部分は、x を整数とするという部分です。
この部分は、命題の対偶をとるときに、一切の変更をせずに、そのまま、使います。
あと、 「①前提となる設定部分」 と「②仮定」の部分を区別する目印として、「このとき」という言葉が使われることが多いです。
そして、「ならば」の前が「②仮定」という中学数学で学習する内容を合わせると、仮定の部分が、「x が 3 の倍数である」ということが分かります。
あとは、「ならば」より後ろの部分が「③結論」ということになります。結論は、最後に残った部分なので、①と②の部分を見つけられると、自動的に決定されます。
では、ここまで命題を細かく構成パーツを捉えることができると、対偶をとったあとの、いはゆる対偶命題がどうなるのかが、はっきりと分かります。
この「仮定と結論を逆にして、それぞれを否定する」ということと、「前提となる設定の部分はそのままにしておく」ということを実行します。
【対偶命題】
x を整数とする。
このとき、
2x が 6 の倍数でないならば、x は 3 の倍数ではない。
これで、はじめの命題の対偶となる命題が完成しました。
実は、はじめにあった命題と、その対偶命題は、真偽が一致します。
したがって、命題を証明するときには、はじめにあった命題か、その対偶命題かのうち、証明しやすい方を証明すれば良いということになります。
「①前提となる設定部分」と「②仮定」の部分が分かれば、このブログの冒頭に書いたように、命題を証明するための解決策が増えます。
そのため、証明しやすい方を自分で選択できるわけです。
次に、背理法でアプローチするときに必要となる、はじめにあった命題の否定の作り方を説明します。
命題 – 仮定 – 結論 :命題の否定
【命題】
x を整数とする。
このとき、x が 3 の倍数 ならば、2x は 6 の倍数となる。
背理法で証明をするときに、はじめにあった命題の結論部分だけを否定した、いはゆる否定命題を考えます。
数学の命題は、「はじめにあった命題」と「その否定命題」のどちらか一方のみが正しいということになります。
そのため、否定命題が正しいとすると、矛盾が出てしまうので、直接的に証明していないけれども、はじめにあった命題が成立しているというのが、背理法の論法です。
結論部分さえ分かれば、それを否定すれば否定命題なので、背理法の方が、否定命題を作りやすいです。では、否定命題です。
【否定命題】
x を整数とする。
このとき、x が 3 の倍数ならば、2x は 6 の倍数ではない。
では、せっかくなので、この否定命題を利用して、背理法ではじめにあった命題を証明してみます。
否定命題の証明
もし、2x が 6 の倍数でないと仮定します。
(つまり、否定命題の方が成立しているとするということです。)
仮定より、
x は 3 の倍数なので、x = 3k (k は整数) という形で表すことができます。
よって、2x = 2 × (3k ) = 6k です。
k は整数なので、2x = 6k は 6 の倍数である。しかし、これは、2x が 6 の倍数ではないということに矛盾します。
ゆえに、背理法より、はじめにあった命題が成立する。 【証明終了】
命題 – 仮定 – 結論 :条件を満たす要素から成る集合
これで、証明が完了しました。
否定命題の方が成立するとすると、矛盾が出てしまうため、はじめにあった命題が成立するというのが、背理法の論法です。
ここからさらに、命題を構成する部分である条件について説明をしていきます。
高校数学を学習するときに、条件を満たす枠組みとなる集合を意識することが大切になります。
確率や整数の分野で、条件を満たす集合 (set) を考え、共通部分や和集合の発想で議論を進めることをよくします。
「整数であり、かつ 3 の倍数である」という条件を満たすものをすべて集めてできた集合が S です。「 | 」よりも右側に条件を書きます。
※ 要素(元)というブログ記事のはじめの方で内包的表記の説明をしています。
ただし、整数全体から成る集合を Z とするというように、あらかじめ集合が指定されているときに、次のような書き方をすることもあります。
S = { x∈Z | x は 3 の倍数 }
この 2 つの表し方は、どちらも同じなので、使っているテキストや授業で使われている表し方で、議論を進めていけば大丈夫です。
条件を満たす集合の練習
x2 = 4 を満たす実数をすべて集めてできる集合を考えてみます。
これは、公立の中学 3 年のときに学習する二次方程式の解をすべて集めた集合を求めるという問題です。
すなわち、4 の平方根をすべて集めてできる集合ということになります。
では、集合を使って表してみます。
{x∈R | x2 = 4} = { -2, 2 }
{ x∈R | x2 = 4} と書くと、少し複雑ですので、答えとしては、
シンプルに具体的に明記した { -2, 2 } の方を書くことにします。
正の平方根が 2 で、負の平方根が -2 ということなので、これら 2 つを集めてできる集合が答えとなります。
ここで、集合について、等しい集合を分かりやすい形に言い換えることができる場合があるということを認識しておいて頂くと良いかと思います。
数学のテキストが分からなく原因として、本の作者が書いた表現と、読者が第一印象で思った集合の表し方が異なるということが挙げられます。
意外と、このことで、数学の本の内容が分からなくなってしまうこともあります。
そんなときには、落ち着いて、集合を言い換えることができないかと考えてみると、解決するときがあります。
▼ 1 点集合で細分化
ここで、さらに与えられた集合を細かく細分化するということをしてみます。
{ -2 } 、{2} という 1 点集合をそれぞれ考えます。
先ほどの { -2, 2 } という集合は、これら 2 つの 1 点集合の和集合として表すことができます。
{-2, 2} = {-2} ∪ {2}
和集合を表す記号「∪」の読み方は「または」です。
二次方程式 x2 = 4 の解を、
x = -2 または x = 2 と言うのは、このように和集合を使って表せるからです。
このように、条件 (condition) を満たすものをすべて集めた集合を考え、共通部分や和集合と論理 (logic) とを関連させる問題は、最近の傾向として増えてきたように思います。
かつ (and) 、または (or) は、エクセルなどやプログラミング言語で使われるので、数学の学習を通じて親しんでおくと、さらに数学以外の範囲へと広げられるので良いかと思います。
整数の条件についての問題練習
5 の倍数全体から成る集合を A 、7 の倍数全体から成る集合を B とするとき、A ∩ B に含まれる要素は、どんな整数かを考えてみます。
A ∩ B の要素ですから、集合 A の要素であり、集合 B の要素でもあるわけです。
a∈A ∩ B とすると、
a∈A なので、a は 5 の倍数です。
※ 集合 A に含まれる条件が 5 の倍数でした。
よって、 a = 5k (k は整数) と表すことができます。
さらに、a∈B でもあるので、5k∈B でもあります。
一方、5k は7の倍数なので、7 で割ると割り切れます。
※ 7の倍数判定法については、リンク先のブログ記事で解説をしています。
ここで、5 は 7 で割り切れないため、k が 7 で割り切れないといけません。
よって、k が 7 の倍数なので、k = 7t (t は整数) と表すことができます。
以上より、a = 5k = 5 × (7t) = 35t となります。
ゆえに、t は整数なので、35t は、35 の倍数です。
したがって、A ∩ B に含まれている要素 a は、35 の倍数ということが分かりました。
ここから、さらに深い命題についての考察は、他の記事で述べることにします。
※ 大学の数学についての記事は、論理と集合を実践的に使い続けています。
高校数学について、不等式の証明に関連して、既に成立している命題を適用するという内容を述べています。
また、高校数学の論理と集合の実践練習として、長方形-定義という記事で、中学2年で学習する図形を使って論理と集合について解説をしています。
これで、今回のブログ記事を終了します。
読んで頂きありがとうございました。