Hom(V,K) – 双対空間 | n次元の線形代数の双対もまたn次元

2023年7月10日

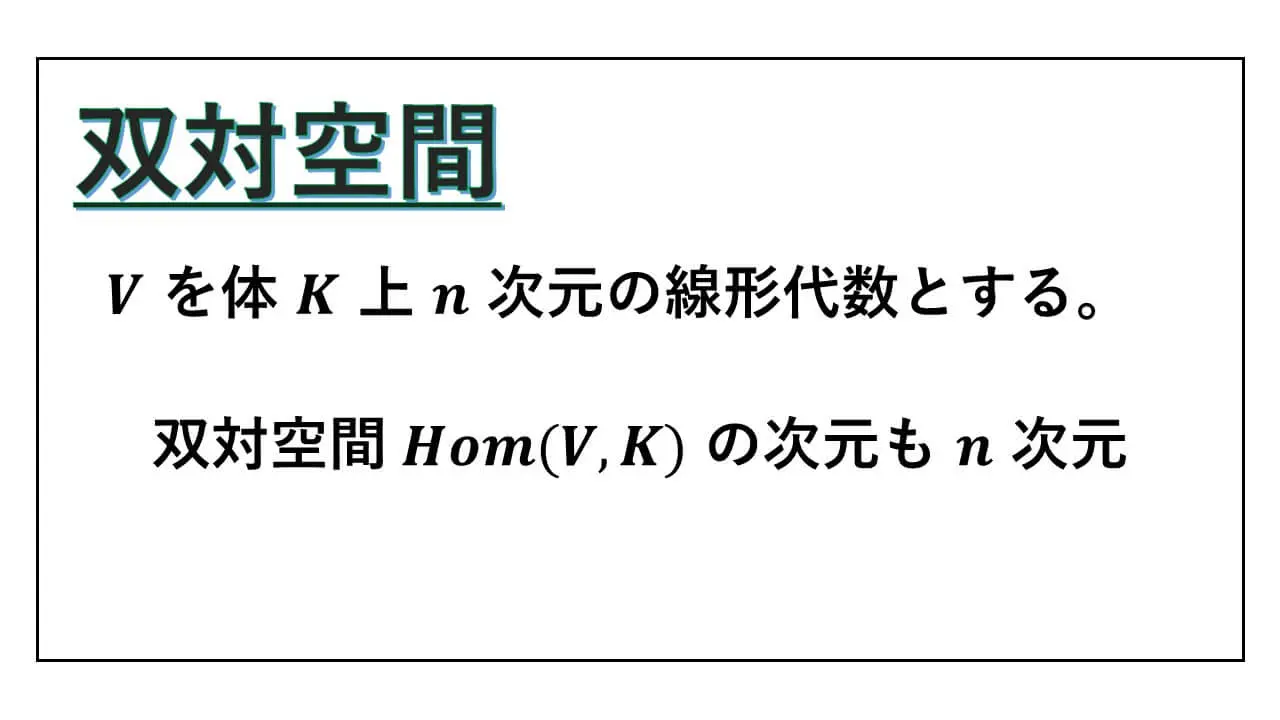
" 双対空間 – Hom(V, K) “もまた線形代数で、有限次元の線形代数の双対空間の次元は、もとの次元と同じです。

双対空間の定義から始めて、この内容を示します。

双対空間は線形代数の公理を満たすということは、定義から導かけます。

双対空間 :定義に基づいて

V ≠ {0_V} を体 K 上の n 次元の線形代数（ベクトル空間）とします。

体 K 自身、体 K 上の 1 次元の線形代数と考えることができます。

K×K → K という体 K から K へのスカラー倍を、
(k, x)∈K×K に対して、
kx を体 K において既に定義されている乗法の値と定義します。

これで、K から K へのスカラー倍が定義され、K において既に定義されている加法を、線形代数としての加法と考えます。

すると、加法とスカラー倍について、K は K 上の線形代数となります。

1∈K を K における乗法単位元とすると、
{1} が 線形代数としての基底となります。

よって、dimK = 1 です。

ここで、Hom(V, K) を V から K への線形写像全体とします。

この Hom(V, K) が、V の双対空間で、K 上の線形代数となっています。

Hom(V,K)の加法とスカラー倍

f, g∈Hom(V, K) に対して、加法とスカラー倍を次のように定義します。

任意の x∈V に対して、
(f+g)(x) = f(x)+g(x),
任意の x∈V, k∈K に対して、
(kf)(x) = kf(x) と定義します。

f+g, kf が、どちらも V から K への線形写像となっています。

この加法とスカラー倍について、線型空間の公理を満たします。

零写像が、加法単位元です。

この Hom(V, K) というベクトル空間のことを、体 K 上のベクトル空間 V の双対空間といいます。

ここからは、双対空間の次元について解説をします。

双対空間 :Hom(V,K)の次元

抽象的な線形代数の一般論を学習した方にとっては、次元は見えたかと思います。

V ≠ {0_V} を体 K 上の n 次元の線形代数とします。

そして、Hom(V, K) は、V から体 K 上の 1 次元のベクトル空間である K への線形写像全体でした。

f∈Hom(V, K) は、行列表示をすると、
K の元を成分とする 1 行 n 列の行列です。

K の元を成分とする 1 行 n 列の行列全体は、行列の加法と、体 K から行列へのスカラー倍について、ベクトル空間となっています。

その次元は、1 × n = n 次元です。

そのため、線形同型である Hom(V, K) の次元も n 次元です。

これで、双対空間の次元が分かったのですが、双対底のことを考え、より詳しく解説を進めます。

1行n列の行列

体 K を n 個で直積集合をつくると、体 K 上の n 次元の線形代数となります。

これを Kⁿ と表すことにします。

k₁, … , k_n∈K について、
(k₁, … , k_n) という 1 行 n 列の K の元を成分とする行ベクトルが Kⁿ です。

実は、Hom(V, K) は、Kⁿ と体 K 上の線形代数として同型になっています。

{v₁, … , v_n} を V の基底とします。

任意の (k₁, … , k_n)∈Kⁿ に対して、
f(v_i) = k_i となる f∈Hom(V, K) が存在することを確かめます。

任意の x∈V は、
x = s₁v₁+…+s_nv_n（ただし、各 s_i∈K）と一意的に表されます。

そこで、
f(x) = k₁s₁+…+k_ns_n と定義します。

この f が、V から K への線形写像となっていることを確かめます。

y∈V も任意に取ると、
y = t₁v₁+…+t_nv_n と一意的に表されます。

f の定義から、
f(y) = k₁t₁+…+k_nt_n

そのため、
f(x)+f(y)
= k₁(s₁+t₁)+…+k_n(s_n+t_n)

一方、x+y∈V について、
x+y
= (s₁+t₁)v₁+…+(s_n+t_n)v_n

基底の一次結合による表し方は一意的なので、f の定義から、f(x+y) は次のようになります。

f(x+y)
= k₁(s₁+t₁)+…+k_n(s_n+t_n)

よって、f(x)+f(y) = f(x+y)

また、u∈K とすると、
ux = (us₁)v₁+…+(us_n)v_n

そのため、
f(ux) = k₁(us₁)+…+k_n(us_n)
= u(k₁s₁+…+k_ns_n) = uf(x)

よって、f(ux) = uf(x) も示せたので、f は線形写像です。

したがって、f∈Hom(V, K)

以上から、
任意の (k₁, … , k_n)∈Kⁿ に対して、f という双対空間の元を対応させることができることが分かりました。

この対応を φ:Kⁿ → Hom(V, K) とします。

φ が単射であることを確かめます。

(k₁, … , k_n), (h₁, … , h_n)∈Kⁿ について、
φ(k₁, … , k_n) = φ(h₁, … , h_n) だったとします。

φ(k₁, … , k_n) を f, φ(h₁, … , h_n) = g と置きます。

x∈V について、
x = s₁v₁+…+s_nv_n（ただし、各 s_i∈K）とすると、
f = g なので、f(x) = g(x) となります。

特に、各 v_i∈V について、
f(v_i) = g(v_i)

v_i = 0v₁+…+1v_i+…+0v_n なので、
k_i = k_i1 = f(v_i)
= g(v_i) = h_i1 = h_i

この i として、1 から n まで同じ議論を繰り返すと、
k₁ = h₁, … , k_n = h_n

よって、
(k₁, … , k_n) = (h₁, … , h_n)

これは、φ が単射であることを示しています。

※ 単射や全射については、全単射という記事で解説をしています。

次に φ が全射であることを示します。

σ∈Hom(V, K) を任意に取ります。

このとき、V の各基底について、
σ(v_i)∈K

そのため、
(σ(v₁),…,σ(v_n))∈Kⁿ

φ((σ(v₁),…,σ(v_n))) = f と置きます。

φ の定義から、
x = s₁v₁+…+s_nv_n（ただし、各 s_i∈K）に対して、
f(x) = σ(v₁)s₁+…+σ(v_n)s_n

各 v_i について、
v_i を {v₁, … , v_n} の一次結合で表すと、
s_i = 1, 他の s_j = 0 となっているので、
f(v_i) = σ(v_i)1 = σ(v_i)

f と σ は、ともに V から K への線形写像であり、基底を構成する各元について、その対応する像が一致しています。

よって、f = σ

つまり、
φ((σ(v₁),…,σ(v_n))) = σ となり、φ が全射であることが示せました。

さらに、この φ が線形写像であることを示します。

そうすると、Hom(V, K) と Kⁿ が線形同型となり、Kⁿ の次元が n なので、双対空間の次元も n ということが分かります。

線形同型写像である確認

(k₁, … , k_n)∈Kⁿ, c∈K とします。

このとき、
φ(c(k₁, … , k_n)) = cφ((k₁, … , k_n)) となることを示します。

V の基底を構成する各 v_i について、その像が一致していることを示せば、二つの線形写像が等しいということになります。

φ((k₁, … , k_n)(v_i)
= k_i1 = k_i です。

そのため、
cφ((k₁, … , k_n)(v_i) = ck_i

c(k₁, … , k_n) = (ck₁, … , ck_n) より、
φ(c(k₁, … , k_n))(v_i)
= (ck_i)1 = ck_i
= cφ((k₁, … , k_n)(v_i)

基底を構成する各元について、対応させている像が一致しています。

よって、
φ(c(k₁, … , k_n)) = cφ((k₁, … , k_n))

次に φ が和を保存することを確認します。

(k₁, … , k_n), (h₁, … , h_n)∈Kⁿ について、
(k₁, … , k_n)+(h₁, … , h_n)
= (k₁+h₁, … , k_n+h_n)

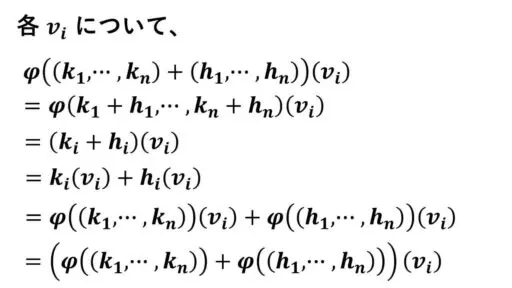
よって、
φ((k₁, … , k_n)+(h₁, … , h_n))
= φ((k₁, … , k_n))+φ((h₁, … , h_n)) が示せました。

これで、φ は線形写像であり、全単射であるということです。

そのため、Hom(V, K) は Kⁿ と線形同型です。

ここまで、ベクトル空間 V の双対空間 hom(V, K) もベクトル空間ということを述べてきました。

hom(V, K) の基底については、双対基底という記事で説明をしています。

これで、今回の記事を終了します。

読んで頂き、ありがとうございました。