ノルム (norm) は計量線形空間の学習の基本に

2022年1月15日

ノルム (norm) は自分自身との内積値です。線形空間において内積が定義されているときに、その線形空間を計量線形空間といいます。

この内積についての特徴的なことを考えるために、ノルムを考えます。

三角不等式を通じて、内積の理解度を向上させつつ基本的な理論も理解できオススメです。

この記事では、内積を高校数学のときに扱ったものよりも、一般的な形で定義を書いています。

線形空間は複素数体上のものを考えます。

この記事では、実数全体から成る集合を R と表し、複素数全体から成る集合を C と表すことにします。

ノルム :まずは大学の内積から

C 上の線形空間 V 上の内積の定義を述べます。

f : V × V → C という写像（関数）が、以下の [1] から [4] を満たすときに、f を V についての内積といいます。

以下、a, b ∈ V について、
複素数 f(a, b) を ＜a, b＞ と表すようにします。
※ ＜a, b＞は複素数なので、その共役複素数は右上に^* をつけて表すことにします。

【内積とは】

[1] 任意の a, b ∈ V に対して、
＜a, b＞= ＜b, a＞^*

[2] 任意の a, b ∈ V と
　任意の α ∈ C に対して、
＜αa, b＞= α＜a, b＞,
＜a, αb＞= α^*＜a, b＞

[3] 任意の a, b, c ∈ V に対して、
＜a, b + c＞= ＜a, b＞+＜a, c＞,
＜a + b, c＞=＜a, c＞+＜b, c＞

[4] 任意の x ∈ V に対して、
＜x, x＞ は 0 以上の実数値であり、
　＜x, x＞= 0 となるのは、x = o のときに限る。
　※ ただし、o は V の加法についての零元。

※ [4] の o ∈ V はベクトル空間 V の零元です。＜x, x＞ = 0 の 0 は実数の 0 です。実数の 0 は複素数の 0 ですが、ベクトル空間の零元は必ずしも数とは限らないので注意です。

これらを満たす内積ですが、実ベクトルについて、高校数学で学習した平面ベクトルや空間ベクトルの内積は、これらの条件にすべて当てはまります。

この内積が定義されている線形空間のことを計量線形空間といいます。

複素数体上の線形空間のときは複素計量線形空間、実数体上の線形空間のときは、実計量線形空間といいます。

具体例

複素数を成分とする行ベクトルである
(a₁, a₂, … , a_n) と
(b₁, b₂, … , b_n) に対して、
a₁b₁^*+a₂b₂^*+ … +a_nb_n^* と定義すると、内積になります。
　
n 次の複素数を成分とする行ベクトル全体は複素数体上の線形空間で、二つの行ベクトルの組に対して、内積を定義しました。
　
この内積の値は、複素数になっています。それぞれの項ですが、右の行ベクトルの成分の共役複素数が掛けられています。
　
高校数学で学習した基本的な複素数の計算から、[1] と [2] と [3] が成立することが確認できます。
　
また、自分自身と内積をとったときには、自分との共役複素数の積が複素数の絶対値の二乗になります。そのため、実数の二乗たちの和ということになります。
　
ゆえに、
a₁a₁^*+a₂a₂^*+ … +a_na_n^*= 0

とすると、
つまり、Σa_ka_k^* = 0 だとすると、
Σ |a_k|² = 0 です。

なので、
a₁ = … = a_n = 0 となります。

このようにして、[4] も成立していることが確認できます。

ノルム :定義

　
計量線形空間 V において定義されている内積を使って、このようにノルムを定義します。内積の定義 [4] から、自分自身との内積は 0 以上の実数値でした。そのため、ルートをつけることができます。

そして、||x|| =1 となっているときに、x ∈ V を単位ベクトルといいます。

随伴について

計量ベクトル空間の議論をするときに、複素数の共役と転置をとるということが絡んでくることが多いです。

記号がややこしいですが、共役複素数を高校の数学で学習したように上にバーをつけて表すことにします。

複素数を成分とする行列 A について、すべての成分の複素共役をとってから、全体を転置した行列を定めることができます。これを A = (a_ij) の随伴行列といい、A* と表します。記号で表すと次のようになります。

　
この n 行 1 列の列ベクトルについての随伴について考えます。

次の内容は、よく混乱されることが多いので、学習し始めたときに注意です。

x*x = ||x||² … ？

ここを詳しく説明します。

x* は転置して 1 行 n 列で、x は n 行 1 列なので、行列の乗法x*xを計算することができます。
x*x は 1 行 1 列の行列です。

x*x = ||x||² の表し方には、1 行 1 列の行列を数とみなすかどうかということが残ります。この同一視をして議論を進めると、書き手と読み手にとっては記述の把握が楽になります。

そういった意味で、
x*x = ||x||² という表し方がされることが多いです。

正当化するには、複素数 α について、(α) という 1 行 1 列からなる行列全体を複素数体上の 1 次元の可換結合代数と考えます。可換体になっています。

「(α) → α」という対応によって、1 行 1 列からなる行列全体は複素数体と同型となります。
※ inclusion （埋め込み） というブログで、同型対応については解説をしています。

このブログ記事では、記述が簡易になるので、
x*x = ||x||² として議論をするようにしています。

これは代数学にある程度の慣れがないと、学習をし始めたときに混乱するので注意です。

ここから、コーシー・シュワルツの不等式を証明します。

コーシー・シュワルツの不等式

複素計量線形空間 V ∋ x, y に対して、次のコーシー・シュワルツの不等式が成立します。

|＜ x, y ＞| ≦ ||x|| ||y||

内積は複素数を値としてとるので、左辺は複素数の絶対値ということになります。

x = o または、y = o とすると、定義から、すぐに成立することが分かります。両辺とも値が 0 となり、等号が成立します。

そのため、以下では、
x ≠ o, y ≠ o として、証明をします。

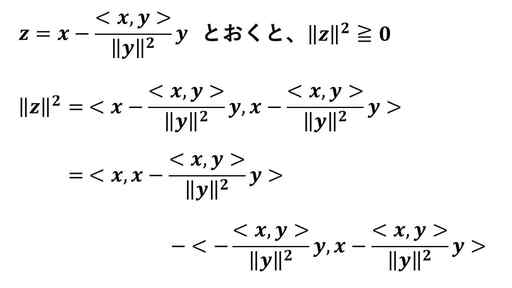
内積の定義を用いて、二つの項に分配をしました。この二つの項をさらに分配をするのですが、複素数値の内積なので、スカラー倍の部分に共役複素数が出てきます。

ただし、分母の ||y||² は 0 以上の実数なので、複素共役をとっても値が変わりません。また、＜x, y＞ は複素数なので、その共役複素数と積をとると |＜x, y＞|² となります。

では、続きの計算です。

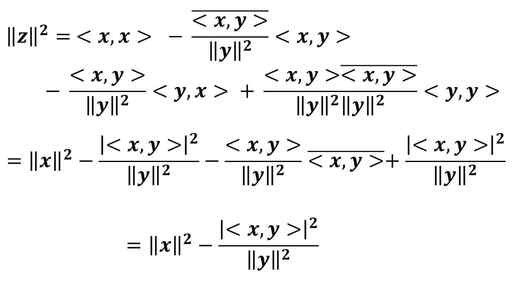
これで、ノルムの二乗の値が非負であるということから、左辺は 0 ≦ ||z||² なので、辿り着いた最後の式の値が非負の実数ということが分かりました。

移項をすると、
|| x ||² ≧ |＜x, y＞|²/ || y ||²
|| x || ≧ |＜x, y＞|/ || y ||
|| x || || y || ≧ |＜x, y＞|

つまり、
|＜x, y＞| ≦ || x || || y || です。

これで、証明が完成しました。

内積は、複素数を値としてとっているので注意です。

また、左右のベクトルを逆にすると、内積の値が共役複素数になることも利用しています。複素数は、その共役複素数と積をとると、絶対値の二乗になるということも使いました。

この有名不等式を利用して、ノルムについての三角不等式を証明します。

そのために、記号を新しく導入します。

複素数 z の実部のことを、Re z と表すことにします。

次の事実を補題の証明で使います。

複素数と、その共役複素数で和を計算すると、その値は実部の二倍となります。

この複素数として、内積 ＜ x, y ＞ を考えます。

また、任意の複素数 z に対して、
Re z ≦ |z| が成立します。

【補題】

＜x, y＞+＜y, x＞
≦ 2 || x || || y ||

＜証明＞

＜x, y＞+＜y, x＞ は内積の定義から、複素数 ＜x, y＞ と、その共役複素数の和なので、
2 Re＜x, y＞ と、実部を 2 倍した値と等しくなります。

よって、
＜x, y＞+＜y, x＞ = 2 Re＜x, y＞
≦ 2|＜x, y＞| ≦ 2 || x || || y ||【証明完了】

最後に、先ほど示したコーシー・シュワルツの不等式を使いました。
内積の絶対値は、ノルムどおしの積の値以下となります。

ノルム :三角不等式

複素計量空間において、次の三角不等式が成立します。

||x + y|| ≦ ||x|| + ||y||

＜証明＞

|| x + y ||² = ＜x + y, x + y＞ の右辺を計算します。

|| x ||² +＜x, y＞+＜y, x＞+ || y || ²
≦ || x ||² + 2 || x || || y || + || y ||²
= (|| x || + || y ||)²

よって、はじめの左辺と合わせると、
|| x + y ||² ≦ (|| x || + || y ||)²

つまり、
|| x + y || ≦ || x || + || y ||

これで、ノルムについての三角不等式が証明できました。

途中で不等号が出ているのが、先ほど証明した補題を適用したからです。

複素計量ベクトル空間について、内積の値が 0 となったときに、二つのベクトルが直交するといいます。

今回の内容は、有限次元計量ベクトル空間において、正規直交基底の存在を証明するときなどに役立つ基本事項となります。

これに関連する内容は、
内積の定義という記事の最後の方で述べています。
※ この記事の前半は高校数学の内容となっています。

それでは、これで今回のブログ記事を終了します。

読んで頂き、ありがとうございました。