退化次数 – 求め方 | null(ヌル)を具体的な例題を使って解説

" 退化次数 “という線形代数で使われる値について、定義を述べた後に、例題を使って具体的に求め方を解説しています。
null と rank をつなぐ定理を具体的な状況で使っているので、内容をつかみやすいかと思います。
細かい抽象的な理論の証明は長く難しいですが、具体的な計算の手順はシンプルなので、線形代数学への親しみをもつ上で、典型的な例題に触れると理解が進みます。
はじめに基礎となる定理を紹介し、退化次数の定義と、それを表す記号の導入を行います。
その後で、具体的な数値を使った例題を通じて、退化次数の求め方を説明します。
退化次数 :nullに関する定理
【次元定理】
V, W を有限次元のベクトル空間(線形代数)とし、f を V から W への線形写像とする。
このとき、
dim(ker f)+dim(Im f)=dim V である。
ここで、
dim(Im f) は、f を表す行列のランク(階数)に等しい。
Im f という記号は、f(V) という V の f による像のことです。
Im f = f(V) は、終集合である W の線形部分空間となっています。
そして、
0∈W という零元について
f-1(0) を ker f と表しています。
ker f = f-1(0) は、始集合(定義域)である V の線形部分空間となっています。
この次元定理は、退化次数とランクをつなぐ定理となっています。
このつながりを意識するために、退化次数の定義を述べます。
退化次数の定義
退化次数の定義をこれから説明します。
ただ、ここで数学では、記号を導入して表すということをすることがあります。
この点について、英語の文法と合わせて円滑に学習をスタートすることが大切です。
退化次数は、日本語における名詞です。
ただ、数学では、退化次数を表す記号として、よく null が使われます。
ker f = f-1(0) の次元が、退化次数の定義です。
null(f) と表されます。
表面的な言葉の差異を気にし過ぎることなく、数学の記号を押さえると、退化次数の求め方が見えてきます。
一連の内容を記号で表すと、
dim(ker f) = null(f) ということになります。
退化次数の定義を押さえると、次元定理によって、f を表す行列のランク(階数)とつながります。
dim(ker f)+dim(Im f)=dim V というのが次元定理でした。
そのため、
退化次数の定義から、
null(f)+dim(Im f) = dim V となります。
ここで、f を表す行列を A とすると、
dim(Im f) は、A のランク(階数)と一致します。
この内容は、ランクの定義から始めて厳密な理論の証明を行うと複雑で難しいものになりますが、この記事では理論を認めて理論を使うことに力点を置いています。
A のランクを、
rank A = rank(f) と表すことにします。
すると、
次元定理は、
null(f)+rank(f) = dim V,
もしくは、
null(f)+rank A = dim V となります。
これで、V から W への線形写像 f について、退化次数とランク(階数)が結びつきました。
そうすると、線形代数学の学習を始めた頃に出てくる、よく知られている行列のランクを求めるということが活用できます。
つまり、f を表す行列 A のランクを求め、V の次元から A のランクを引くと退化次数となるというわけです。
では、この内容を具体的に実践します。
画像で述べている行列 A と、A が表す線形写像 fA について、退化次数を具体的に求めます。
可換体 F 上の 4 次元ベクトル空間 V から F 上の 3 次元ベクトル空間 W への線形写像を表す行列が A という設定です。
F4 の元である 4 行 1 列の列ベクトルに左から A を掛けると、3 行 1 列の列ベクトルになります。
これが、fA : V → W への線形写像を行列で表したものになります。
退化次数 – 求め方 – 例題
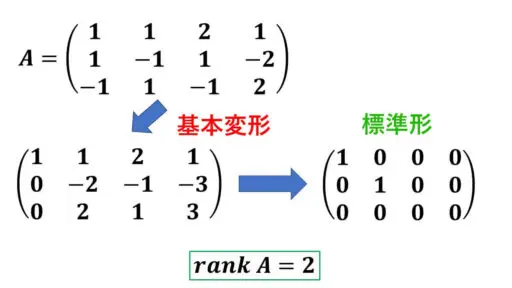
この 3 行 4 列の行列 A が表す線形写像を fA と表すことにします。
fA : V → W を求めたいわけです。
そこで、よく知っている行列の基本変形をして、A のランクを求めることからスタートします。
行列の基本変形を有限回だけ行うと、図に記している標準形の形になります。
標準形を見ると、2 行 2 列の単位行列が一つのブロックとなっていて、残りのブロックの部分は全て零行列となっています。
※ ブロック分割という記事で行列の区分けについて基礎的なことを解説しています。
標準形にすると、
2 次の単位行列が現れているので、
rank A = 2 ということです。
つまり、rank(fA) = 2 です。
ここで、
rank(fA) = dim(Im fA) だったので、
dim(Im fA) = 2 です。
定理の適用
これで次元定理を使うチャンスが到来しました。
dim(ker f)+dim(Im fA)=dim V という等式でした。
今、dim V = 4 で、
dim(Im fA) = 2 という状況です。
よって、
dim(ker f)+2 = 4 です。
これで、
dim(ker f) = 2 と分かります。
この ker f の次元が、退化次数の値でした。
すなわち、
null(fA) = dim(ker f) = 2 です。
これで、退化次数を求めることができました。
【求め方まとめ】
行列を基本変形して、行列のランクを求めるという線形代数学を学習し始めた頃に学習する内容から、スタートします。
標準形にしてランクを求めたら、次元定理を使って、カーネル(核)の次元を計算します。
この次元が、退化次数です。
行列のランクを計算することで、線形写像の核についての次元が求まるので、線形写像を行列で表示したメリットが実感できる内容となっています。
最後に null について述べておきます。
退化次数 :nullについて
先ほどの例題では、核の次元が 2 でした。
そこで、ker fA の基底を、
{v1, v2} とします。
dim V = 4 だったので、あと 2 個のベクトルを適切に加えて基底を延長し、V の基底とすることができます。
v3, v4 を加えて、
{v1, v2, v3, v4} を V の基底とします。
V の各元は、基底の一次結合によって一意的に表すことができます。
x∈V とすると、
k1, … , k4∈F が存在し、
x = Σi kivi と表せます。
この x を線形写像 fA で移してみます。
fA(x) = fA(Σi kivi)
= Σi kifA(vi) となります。
ここで、v1, v2 が ker fA の元だったことから、fA で移すと W の零元となり、消えます。
つまり、fA(v1) = fA(v2) = 0 です。
この消えてしまうことが、退化という感覚になります。
fA(x) = Σi kifA(vi)
= 0+0+k3fA(v3)+k4fA(v4)
= k3fA(v3)+k4fA(v4) です。
4 個ある V の基底を構成する元の中で、fA で移したときに退化してしまう元の個数が 2 ということです。
これが、null(fA) = 2 ということです。
この他にも退化次数を見ることができる具体例はたくさんあります。
線形写像が和とスカラー倍を保存するということと、基底の一次結合を合わせて、関連する内容について述べました。
線形代数学の分野で扱われる内容は多いので、線形写像に関する内容について、記事を置いておきます。
関連する記事
■ 基底変換行列
線形変換について、基底を取り替えるということを表す行列について解説しています。
※ 線形写像の始集合と終集合が同じベクトル空間となっているときに、その写像を線形変換といいます。
■ End(V)
エンドモルフィズムが全体が成す環で、線形代数学と環論に関わる内容になります。
これら二つは、線形代数についての理論の証明が中心となっています。
具体的な線形変換の内容については、次の記事で解説をしています。
■ 微分作用素
これは、シンプルなベクトル空間を用意して、微分するという操作を行列で表示し理解を深めることを狙った内容となっています。
この記事では、無限次元ベクトル空間の例について述べています。高校から使っていた実数列全体が、それに該当します。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。