はさみうちの定理 もしくは原理 | 関数の極限と図形

" はさみうちの定理 (原理)"は、サンドイッチのように対象とする関数をはさみます。
下からの評価と上からの評価が同じ値に収束するときに、はさまれている真ん中の関数も、その値に収束するということを意味している定理です。
この内容は、図形的な内容と融合させて使うときもあるので、視覚的なアプローチも大切です。
高校数学IIIで扱われる典型的な例を使って、解説をしています。
また、記事の最後で、はさみうちの定理を大学数学で使われる定義に基づいて証明しています。
高校一年のときに学習した三角比の内容と、数学IIIの極限の内容で、有名な極限の公式を導きます。
はさみうちの定理 :事前の知識
関数 f(x) と g(x) について、
f(x) ≦ g(x) … (1)
となっていたとします。
x → ∞ のときに、
f(x) → α , g(x) → β が、それぞれの収束値だとすると、(1) の条件の下では、α ≦ β となります。
このことと合わせて、次のように下から f(x) で評価され、上から g(x) で評価されている関数 h(x) の収束値を考えます。
【はさみうちの定理】
f(x) ≦ h(x) ≦ g(x) であり、x → ∞ のときに、f(x) と g(x) がともに α に収束しているとき、h(x) も必ず α に収束する。
f(x) ≦ h(x) ≦ g(x) とサンドイッチされていて、f(x) と g(x) がどちらも α に収束するときに、はさまれている真ん中の h(x) も必然的に α に収束するという感覚的に覚えやすい定理です。
この定理は、微分積分の計算でよく使われます。また、図形的な考察と合わせて考えるときもあるので、図の内容を数式でうまく表現することも大切になります。
ときには、高校一年の頃に学習した不等式の性質を使った式の書き換えが役に立つこともあります。
論理的な客観的な式の書き換えと、図形的な情報をうまく合わせてアプローチする問題には慣れておくと良いかと思います。
はさみうちの定理 :図形への応用
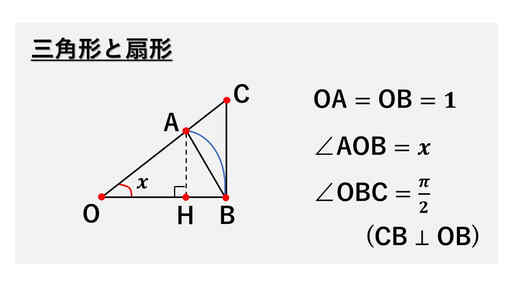
この図の三角形と扇形の面積について、はさみうちの定理を使うことで、有名な不等式を導くことができます。
OA もしくは OB は扇形の半径で、長さが 1 という状況です。
x の大きさによって、場合分けをして、議論を進めます。
【1】0 < x < π/2 の場合
三角形 OAB の面積は、扇形OAB の面積よりも小さくなっています。
そして、扇形 OAB の面積は、三角形 OAB の面積よりも小さくなっています。
※ 真ん中が下からと上からにはさまれているので、定理を使うチャンスです。
三角形 OAB の高さは AH で 1 × sin x なので、sin x です。
そして、線分 BC の長さは、tan x を利用して、次のようにして表すことができます。
tan x = BC ÷ OB
= BC ÷ 1 = BC
つまり、BC = tan x となっています。
これらのことから、面積について、次のような不等式が得られます。
1/2 × 1 × sin x
< 1/2 × 12 × x
< 1/2 × 1 × tan x
※真ん中は扇形の面積を求める公式
それぞれの辺を 2 倍すると、
sin x < x < tan x
tan x = sin x ÷ cos x なので、
1 < x/sin x < 1/cos x
逆数をとると、
1 > sin x / x > cos x
x → +0 のとき、cos x → 1 なので、
はさみうちの定理から、
sin x / x → 1 です。
今度は、左極限について考察をします。
【2】- π/2 < x < 0 の場合
x = – θ と置き換えます。
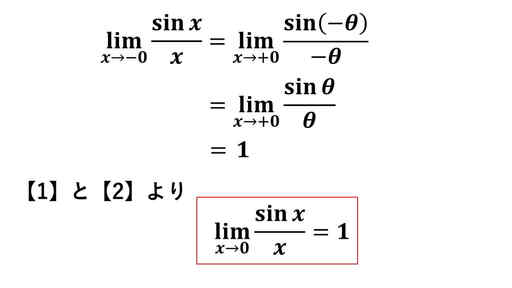
右極限と左極限が一致したので、これが関数の極限となります。
よく使う sin の極限の公式が導けました。
この内容は数学3の内容ですが、
和積変換公式など、数学2で学習する三角関数についての公式もよく使われるので、合わせて押させておくと良いかと思います。
また、証明で用いた扇形についての公式やラジアンについての定義は、弧度法という記事で解説をしています。
では、先ほどの内容をもう少し説明します。
補足説明
場合【2】のときに、x を左から 0 に近づけました。
このときに、θ は右から 0 に近づくことになります。
右から 0 に近づくときについては、既に場合【1】において示していたので、【1】の内容を適用しました。
既に示している場合に帰着させるのは、数学でよく使う手です。
導いた公式を使う例
導いた公式を利用して、
x → 0 のときに、sin 4x / x の収束値を求めてみます。
sin 4x / x
= sin 4x / 4x × 4
そして、x → 0 のとき 4x → 0 なので、
導いた公式より、4x → 0 のとき、
sin 4x / 4x → 1
この値に 4 を掛けたものが求める値なので、
sin 4x / x → 4
これが求める収束値です。
sin の極限の公式は、分母の変数と角の大きさを表す変数を同じにしておいて適用します。
そのために、分数全体に実数を掛けることで、分母の変数を調整することが大切になります。
はさみうちの定理 :関数の極限
はさみうちの定理のついでに、関数の極限について述べておきます。
x → a としたときに、f(x) が f(a) に収束するということの定義を正確に述べておきます。
x → +a と x を a に右から近づけたときに関数 f(x) が収束し、かつ、x → – a と左から近づけたときにも f(x) が収束し、しかも両方の収束した値が等しい。
これが、x = a において、f(x) が f(a) に収束するということの定義です。
右極限と左極限が同じ値に収束するということを確認することになります。
なお、右極限と左極限が存在していたとしても、値が異なるときには、x → a のときに関数 f(x) が収束していないということになります。
※ x = a において、右極限と左極限が等しい値であるときに、x = a において関数 f(x) が微分可能であるといいます。
ロルの定理を証明するときにも、この微分可能であるという条件が効いてきます。
x = a において関数 f(x) が微分可能であるときに、その右極限(もしくは左極限)の値のことを f'(a) と表します。
具体例で確認
実数値関数 f(x) = (x2 – x) ÷ |x| (x は実数) について、x = 0 において微分可能かどうかを調べてみます。
左から x を 0 に近づけると、f(x) は 1 に収束します。そのため、左極限は 1 です。
しかし、x を右から 0 に近づけると、f(x) は – 1 に収束します。
したがって、右極限は -1 で、左極限は 1 なので、一致していないので、x = 0 において微分可能ではないということになります。
この内容を式で述べておきます。
x < 0 の範囲で、左から x を 0 に近づけます。
x < 0 の範囲では | x | = -x に注意すると、
f(x) = (x2 – x) ÷ ( – x)
= – x + 1 → 1
一方、x > 0 の範囲において、x を右から 0 に近づけます。
| x | = x となっていることに注意すると、
f(x) = (x2-x) ÷ x
= x-1 → -1
よって、 f(x) は x = 0 において、微分可能ではないということになります。
微分可能だと連続
【定義】
h → 0 のとき、
{f(a + h)-f(h)} ÷ h が収束するとき(右極限と左極限が同じ値に収束するとき)、x = a において、関数 f(x) が微分可能であるといいます。
x → a のときに、
{f(x)-f(a)} ÷ (x-a) が収束すると言い換えることができます。
x = a において、右極限と左極限が同じ値に収束しているということが微分可能の定義です。
x = a において、関数 f(x) が微分可能であるときに、f(x) は x = a において連続ということが証明できます。
これは、連続性を判定するときの一つの方法になるので、押さえておくと良いかと思います。
ちなみに、逆である「連続ならば微分可能」ということは、一般に成立しません。
g(x) = | x | という関数は、x = 0 において連続ですが、先ほどと同じように右極限と左極限を考えると、それらが一致しません。
g(x) = | x | を連続だけれども、微分可能ではない例として挙げておきます。
【例】
■ f(x) = x2 は x = 0 で微分可能
■ g(x) = |x| は x = 0 で微分可能ではない
では、微分可能だと連続になっていることの証明を述べて、このブログ記事を終了します。
連続であることの証明
【命題】
関数 f(x) が x = a で微分可能であるとき、f(x) は x = a において連続である。
<証明>
x → a のときを考えます。
f(x)-f(a)
= (x-a) × {f(x)-f(a)}/(x-a)
→ 0 × f'(a) = 0
したがって、x → a のとき、
f(x) は f(a) となっているので、x = a において、f(x) は連続です。【証明完了】
大学の数学内容の記事も投稿していまして、イプシロンデルタ論法という関連記事で、関数の連続性について解説しています。
ここからは、大学数学で用いられる定義に基づいて、はさみうちの定理を証明します。
はさみうちの定理 :大学数学で証明
はさみうちの定理を数列について証明してから、関数について証明します。
定義域が離散的な関数(写像)である数列については、εN法を用いて数列の極限値が定義されています。
実数全体を定義域とする関数については、連続性のことを考慮して、εδ論法を用いて関数の極限値が定義されます。
【数列の極限値の定義】
実数を各項の値とする数列 {an} と、実数 r が与えられたとする。
「任意の正の実数 ε に対して、ある自然数 N が存在し、
N 以上の任意の自然数 n に対して、
|an-r| < ε 」が成立するとき、r を数列 {an} の極限値という。
(もしくは、数列 {an} が r に収束するという。)
この数列の極限値の定理に基づいて、はさみうちの定理を数列について証明します。
【定理1】
数列 {an}, {bn}, {cn} について、
各自然数に対し、an ≦ bn ≦ cn となっているとする。
そして、数列 {an}, {cn} が両方とも実数 r に収束しているとする。
このとき、数列 {cn} も実数 r に収束する。
<証明>
任意の正の実数 ε が与えられたとする。
数列 {an}, {cn} が両方とも実数 r に収束しているという仮定より、ある自然数 N, M が存在して次が成立します:
N 以上の任意の自然数 n に対して、
|an-r| < ε,
M 以上の任意の自然数 n に対して、
|cn-r| < ε
すなわち、絶対値の定義から、
N 以上の任意の自然数 n に対して、
r-ε < an < r+ε … (1)
r-ε < cn < r+ε … (2)
ここで、K = max{N, M} と置きます。
K 以上の任意の自然数 n について、仮定より、
an ≦ bn ≦ cn … (3)
(1), (3) より、
r-ε < an ≦ bn … (4)
(1), (3) より、
bn ≦ cn < r+ε … (5)
今、(4) かつ (5) が成立しているので、
r-ε < bn < r+ε となります。
r を移項すると、
-ε < bn-r < ε です。
絶対値の定義から、
K 以上の任意の自然数 n について、
|bn-r| < ε となっています。
これで、数列の極限値の定義から、
数列 {bn} が実数 r に収束することが示せました。【証明完了】
証明で使った max については、
max min という記事で定義を具体例を用いながら解説しています。
次に、実数全体の空ではない部分集合を定義域とする関数について、極限値を定義し、はさみうちの定理を証明します。
はさみうちの定理を関数について証明
【関数の極限値の定義】
実数全体の空集合ではない部分集合 S を定義域とする実数値関数を f と、実数 a と r が与えられたとする。
このとき、「任意の正の実数 ε に対して、ある正の実数 δ が存在し、
|x-a| < δ を満たす任意の S の元 x に対して、
|f(x)-r| < ε 」が成立すれば、実数 a において、f は極限値 r をもつという。
(x が a に近づくとき、f(x) が r に収束するという。)
数学3で、x → a のとき、f(x) → r と述べていたことを、大学数学で正確に表すと、このようになります。
数直線上で、x が a に近づくには、a より大きい範囲から x が a に近づくという右からの近づき方と、a より小さい範囲から x が a に近づくという左からの近づき方があります。
どちらの近づき方であっても、極限値の定義から、同じ値に収束しなければならないことを意味しています。
また、定義域 S を実数全体の空集合ではない部分集合としましたが、S として実数全体自身を考えることもできます。
それでは、はさみうちの定理を証明します。
【定理2】
実数全体の空集合ではない部分集合 S において、関数 f(x), h(x), g(x) が定義されていたとする。また、a∈S と実数 r が与えられたとする。
そして、任意の t∈S に対して、
f(t) ≦ h(t) ≦ g(t) となっていたとする。
このとき、
関数 f(x) と g(x) が x = a において実数 r に収束しているとすると、
関数 h(x) も x = a において実数 r に収束する。
<証明>
任意に正の実数 ε が与えられたとする。
関数 f(x) と g(x) が x = a において実数 r に収束しているという仮定から、関数の極限値の定義より、次が成立します:
ある正の実数 δ1 が存在し、
|x-a| < δ1 を満たす任意の x∈S に対し
|f(x)-r| < ε,
ある正の実数 δ2 が存在し、
|x-a| < δ2 を満たす任意の x∈S に対し
|g(x)-r| < ε
ここで、δ3 = min{δ1, δ2} と置きます。
|x-a| < δ3 を満たす任意の x∈S に対し、
r-ε < f(x) < r+ε … (1)
r-ε < g(x) < r+ε … (2)
任意の t∈S に対して、
f(t) ≦ h(t) ≦ g(t) となっているという仮定から、
|x-a| < δ3 を満たす任意の x∈S に対し、
(1) より、r-ε < f(x) ≦ h(x) です。
すなわち、|x-a| < δ3 を満たす任意の x∈S に対し、
r-ε < h(x) … (3)
同様に、(2) を用いると、
|x-a| < δ3 を満たす任意の x∈S に対し、
h(x) ≦ g(x) < r+ε … (4)
(3), (4) より、
|x-a| < δ3 を満たす任意の x∈S に対し、
r-ε < h(x) < r+ε となります。
絶対値の定義から、
|x-a| < δ3 を満たす任意の x∈S に対し、
|h(x)-r| < ε です。
関数の極限値の定義から、
x = a において、h(x) は r に収束します。【証明完了】
これで、はさみうちの定理の証明ができました。大学の数学では原理ではなく証明される定理となります。
高校の数学では、証明なしで用いられるので、はさみうちの原理という名前になっています。
大学で扱うイプシロンデルタ論法については、他の記事で解説をしています。
これで、今回のブログ記事を終了します。
読んで頂き、ありがとうございました。