期待値 E(X) | 離散型確率変数を具体例で理解
" 期待値 E(X) " は、確率変数の単元で出てきます。確率変数の単元は、かなり学習をし始め易いので、オススメです。
しかも、型にはまった期待値を計算する問題がよくテストに出るので得点をする機会が増えるかと思います。
どうして学習をし始め易いかというと、中学で学習する確率の内容を具体例として用いることで、抽象的な確率変数に関連する内容が見やすくなるからです。
難しそうな内容は、中学内容を具体例にして様子を見ると理解するチャンスになります。
データの分析で学習する内容と合わせて、確率変数、そして期待値を押さえておくと、得点をする幅が広がるかと思います。
最後に二項分布（ベルヌーイ分布）について述べています。
期待値 E(X) :確率変数とは
【確率変数の期待値】
P(X=x1)=p1,P(X=x2) = p2, … , P(X=xn) = pn で、これらの確率を全て足すと、合計が 1 だとします。
このとき、
x1p1+x2p2+…+xnpn = Σk xkpk を確率変数 X の期待値といいます。
期待値を表す記号は、E(X) です。
確率変数の学習をし始めると、いきなり抽象的な内容が出てきます。
一般の自然数 n で、シグマ記号を使って期待値が述べられることもあります。
そこで、シンプルな具体例を使い、確率変数を具体的に見ていきます。
ちなみに、期待値は上に描いている表の各列について、上下を掛け合わせてできた項たちを全て足し合わせたものです。
したがって、上の確率変数の表の意味が分かれば、機械的に計算をすると期待値の値が得られるということになります。
具体例で確率変数を理解する
確率変数 X がとる具体的な値たちは、小文字で x1 というように表されます。
この説明だけだと、難しそうなので、具体的な設定で、説明をしていきます。
【設定】
2 枚の五円玉を同時に投げるときを考えます。
・裏が出た五円玉の金額の合計が確率変数 X のとる値とします。
※ それぞれの五円玉は区別し、裏が出る可能性は同様に確からしいとします。
ここで、X のとり得る可能性は、次の三つとなります。
・どちらも表で合計 0
・1 枚だけが裏で合計 5
・2 枚とも裏で合計 10
上の画像の確率変数は抽象的ですが、具体的には、これらの可能性を表で表しているだけです。この具体例では、確率変数のとる値の可能性が 3 パターンなので、n = 3 のときとなります。
そして、それぞれの値となるときの確率を求めて、X の値を書いた列の下側に書きます。
※ 2 枚の五円玉は区別をしているので、起こり得る場合の総数は 4 通りです。
「どちらも表で合計 x1 = 0」となるときの確率
（表, 表）の 1 通りなので、p1 = 1/4
「どちらも表で合計 x2 = 5」となるときの確率
（表, 裏）と（裏, 表）の 2 通りなので、
p2 = 2/4 = 1/2
※ x2 = 5 とは、1 枚だけが裏なので、金額の合計が 5 + 0 = 5（円）だからです。
この 5 という値を確立変数 X がとる 2 通り目の値なので、x2 としています。
では、次に、確率変数 X がとる 3 通り目の可能性である x3 に関連する確率を求めます。
「2 枚とも裏で合計 10」となるときの確率
→ （裏, 裏）の 1 通りだけなので、p3 = 1/4
以上の確率変数がとる値たちと、それぞれが起こる確率をまとめます。
そして、X の期待値を計算します。
P(X=0) = 1/4, P(X=5) = 1/2,
P(X=10) = 1/4 より、
期待値の定義から、
E(X) =
0・1/4+5・1/2+10・1/4 = 5
確率をすべて足し合わせると、1 になるので、ミスをしていないかを軽く確かめるときに使えます。
また、この手のシンプルな内容で期待値を計算することで、シグマ記号の意味の理解へも良い影響があるかと思います。
※ シグマ記号の解説はリンク先の記事に書いています。
期待値 E(X) を求めるときに、
敢えてシグマ記号を用いると、
x1p1 + x2p2 + x3p3
= Σk xkpk
(kは1から3まで動く) が、シグマ計算です。
どのような計算になっているのかを押さえる良い練習にもなります。
期待値 E(X) そして V(X)
【確率変数の分散】
確率変数の期待値 E(X) = m のとき、X の分散を V(X) と表す。
そして、V(X) の正の平方根を X の標準偏差といい、σ(X) と表す。
分散が分かれば、その値にルートをつけると標準偏差になります。ただ、まだ分散の定義を述べていません。分散の定義の前に、確率変数の単元での記号の使い方を述べておきます。
m という実数があったときに、確率変数 X から、新しい確率変数 X － m を定義することができます。
このように書くと、意味が分かりにくいですが、これも具体例を使うとすぐに理解できます。
※ 複二次式の例題という記述で文字の置き換えを解説していますが、今回は確率変数の置き換えです。
先ほどの具体例を使って、期待値 E(X) = 5 だったので、5 という実数を使います。新しい確率変数である X － 5 がどのような値たちをとるかを述べます。
結論から書くと、X がとる値たちから 5 を引いた値たちが、確率変数 X － 5 がとる値たちになります。
すなわち、
x1 － 5, x2 － 5, x3 － 5 たちです。
x1 = 0, x2 = 5, x3 = 10 だったので、
確率変数 X － 5 のとる値たちを具体的に計算でき、
－5, 0, 5 だと分かります。
これらが、確率変数 X － 5 のとる値たちです。
そして、これらの値を二乗したものたちが、確率変数 (X － 5)2 のとる値たちとなります。
X のとる値たちから、一斉に 5 を引いてできた数たちは、分散の定義に関わってきます。ここまで、具体的に求めておくと、分散の定義が認識しやすいです。
【V(X) の定義】
確率変数 X の期待値が 5 のとき、
確率変数 (X － 5)2 の期待値を、X の期待値 5 からの分散という。
※ 分散を表す記号は V(X) です。
では、具体的な値たちを求めているので、分散の定義の通りに計算してみます。なお、分散の値が求まると、それにルートをつけると標準偏差の値となります。
具体例で、p1 = 1/4, p2 = 1/2, p3 = 1/4 だったので、次のように分散を計算できます。
＜X の期待値 5 からの分散＞
(－5)2 ・1/4 + 02 ・ 1/2 + 52・1/4
したがって、
V(X) = 25/4 + 0 + 25/4 = 12.5
このように、確率変数 X がとる値たちと、期待値が 5 と分かっている状況だと、分散を具体的に計算することができます。
一般的な定義は、シグマを使ったものですが、「まとめ」として書いておきます。
期待値 m のときの V(X)
V(X) = E((X－m)2)
= Σi=1 (xi－m)2pi
= (x1－m)2p1+(x2－m)2p2+…+(xn－m)2pn
分散が求まると、それにルートをつけると標準偏差になります。
つまり、σ(X) = {V(X)}1/2 です。
一般的な定義です。
先ほどの具体例では n = 3 のときを扱いました。
定義の内容は、確率変数 (X － m)2 の期待値が、期待値 m からの X の分散 V(X) の値です。
この分散を求めるためには、確率変数 X を変数変換します。
確率変数 (X － m) という確率変数を新しく作ります。そして、さらに変数変換をします。
確率変数 (X － m) がとる値たちをすべて二乗したものを、値とする確率変数 (X － m)2 を作ります。
具体例だと、(－5)2, 02, 52 でした。それぞれの起きる確率が 1/4, 1/2, 1/4 だったので、期待値の定義の通りに掛け合わせてできた項をすべて足しました。
この内容をシグマを使って一般に表しているのが、上の式です。
シグマ計算に慣れるためにも、具体例で様子を見ることは役に立ちます。
(x1 － m)2 → (0 － 5)2
(x2 － m)2 → (5 － 5)2
(x3 － m)2 → (10 － 5)2
具体例では、n = 3 のときだったので、三つの項が現れていました。
そして、これら (X － m)2 という確率変数がとっている各値 (xi － m)2 の起きる確率 pi との積を計算します。これらの積が、シグマ計算に現れる項の 1 つ 1 つとなっています。
このようにして期待値 m からの分散 V(X) が定義されています。確率変数 (X － m)2 の期待値が、分散の値です。
ただ、分散の値は、次の値と同じになることが証明されます。シグマ計算のルールの通りに計算をすることで、証明ができます。
V(X)を求める他の方法
【他のV(X)の求め方】
確率変数 X の期待値が m のとき、分散は次のように書き換えることができます。
V(X) = E(X2) － m2 となります。
これは、次のようにシグマ計算のルール通りに計算をすることで導かれます。
＜証明＞
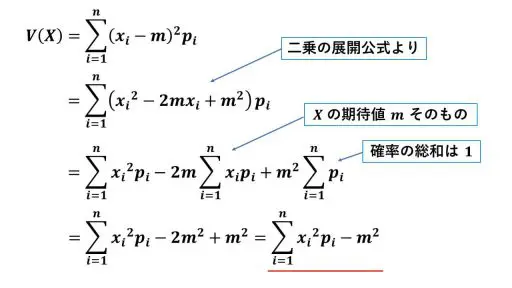
最後に辿り着いた赤色の線を引いている部分は、E(X2) － m2 のことです。
先ほど、シグマの計算のルールから導かれると書きましたが、期待値の定義を使って見た目を変形するのもポイントになります。
確率変数 X2 がとる値 xi に、それが起きる確率 pi を掛け合わせてできた項が xipi です。
これらの項を i が 1 から n まで足し合わせたものがシグマの部分です。そして、それは X2 の期待値の定義の通りです。
このため、赤色の部分のシグマの値は、E(X2) です。
あと、この手の証明で、たまに使うこととして、「全ての確率の和が 1」には注意です。中学の数学の確率のときから知っている内容ですが、シグマを使うと下から二番目の式のようになります。
p1 + p2 + … + pn =1 がシグマ記号の形で表れてくることがあるので、ここで証明が止まってしまわないように、経験を積んでおくと良いかと思います。
【関連する記事】
■ 分散
高一の統計分野の内容となります。
■ 二項分布
シグマと合わせて数B の確率変数を考慮し、期待値についての具体的な例を使って解説をしています。
■ 相関係数
－1 以上 1 以下の範囲となることの証明を解説しています。
最後に、化学基礎で出てくる期待値について触れておきます。
同位体と原子量について
高校の数学で学習した内容が、高校の化学で使われることもあります。
そこで、確率と期待値の内容が使われている内容にも触れておきます。
同位体といって、同じ H 原子であっても質量数が異なるものが自然界には存在します。
1H と 2H というように同じ H だけれども、質量数が異なるものが同位体です。
ここで、自然界の中から H 原子を無作為に取り出すという操作を考えることにします。
H 原子を 1 個だけ取り出したときに、1H である確率を 1H の存在率と化学では述べられたりします。
1H が 1 個についての重さのことを相対質量といったりします。
数学で、箱の中から球を取り出す確率と同じ内容ですが、用語が化学で使われている用語なので難しく感じるかもしれません。
こんなときは、具体的な内容で練習しておくと良いかと思います。
相対質量の期待値
【練習問題】
1H の相対質量が 1.01 で存在率が p とします。
また、2H の相対質量が 2.01 だとします。
自然界に H 原子の同位体が、これら以外には存在しないとします。
このとき、H 原子の原子量を定数 p を用いて表してください。
自然界から無作為に H 原子を 1 個だけ取り出したときに、期待される質量を H 原子の原子量といいます。
つまり、H 原子 1 個を取り出したときの重さの期待値が原子量というわけです。
これを定数 p を用いて表そうということです。
前提となる「自然界に H 原子の同位体が、これら以外には存在しない」という内容から、余事象の確率が使えます。
1H の存在率が p なので、
2H の存在率が (1－p) となります。
H 原子 1 個を取り出したときの重さの期待値を計算するので、期待値の定義の通りに計算をします。
1.01p+2.01(1－p) が、求める値です。
文字式の計算をすると、
2.01+1.01p－2.01p
= 2.01－p となります。
高校の化学の問題集では、相対質量がもっと細かい小数になっていて、存在率が文字でなく小数で与えられていると思いますが、計算しやすいようにしておきました。
あくまで、確率の期待値の内容が、化学でどう使われているのかに焦点を当てるために、計算のハードルを下げた内容ですので、ご了承ください。
化学と数学が絡む内容については、アボガドロ定数という記事も投稿しています。
また、食塩水の濃度という記事では、最後に数列の関係式の内容に言及しています。
この記事では、数学IIIの逆関数の内容にも言及をしています。
それでは、これで記事を終了します。
読んでくださり、ありがとうございました。