相関係数 r の範囲は－1以上1以下であることの証明

2023年1月28日

相関係数 r の値の範囲は－1以上1以下になります。

高一の統計分野で学習する事実ですが、有名な不等式を利用して、証明ができます。

標準偏差と共分散を用いて定義される相関係数の範囲を示すことは、証明問題の良い練習になるかと思います。

※散布図とともに扱われる相関係数についての発展内容になります。

シュワルツの不等式という有名な不等式の証明から始めます。

シュワルツの不等式を使って、相関係数の値の範囲を導きます。

相関係数 :まず有名不等式の証明

この有名不等式の証明をするときに、無理関数のとる値と不等式についての知識が大切になります。

中学の数学で学習するルートをとるということについての性質になります。

実数 x について、g(x) を x にルートをつけた値と定義します。数学IIIでいうところの 1/2 乗するということです。

このとき、0 ≦ a ≦ b ならば、
0 ≦ g(a) ≦ g(b) となります。

g(a) は、a にルートをつけた値、つまり、a を 1/2 乗した値です。

g(b) は、b にルートをつけた値、つまり、b を 1/2 乗した値です。

定義域と値域の対応を考えたときに、定義域での大小関係のままになっています。

ここまでの内容に留意しつつ、有名不等式を証明します。

有名不等式の証明

f(x) = Σ_i=1n (p_ix+q_i)² とします。

p_i, x, q_i (i = 1, 2, … , n) は実数なので、
f(x) ≧ 0 です。

括弧の二乗の部分を展開します。

f(x) = Σ_i=1n{(p_i)²x²+(2p_iq_i)x+(q_i)²}
= (Σ_i=1np_i²)x²+2Σ_i=1np_iq_ix+(Σ_i=1nq_i²)

このように、f(x) という関数を定義します。p_i と q_i はシュワルツの不等式に使われる実数です。

実数を二乗すると、その値が 0 以上ということから、f(x) は 0 以上であるということが分かります。

シグマ記号を使って、端的に内容を述べていますが、i に 1 から n までの値を代入してできる n 個の中括弧の項たちの和を意味しています。

そのため、x², x, 定数項という降べきの順に同類項を整理でき、f(x) を表す式は、赤色で書いた式となっています。

さらに、(Σ p_i²) という x² の係数は、実数を二乗したものの和なので、値は 0 以上ということになります。

ここで、もし、x² の係数が 0 だとすると、各 i について、p_i = 0 ということになります。
※ p₁² + ・・・ + p_n² = 0 ということは、どの p_i も 0 ということです。

このとき、シュワルツの不等式の左辺と右辺がどちらも 0 となり、求める不等式が等号で成立ということになります。

したがって、以下、 x² の係数が 0 ではないという場合について、議論をします。

x² の係数が 0 でないということは、f(x) が二次関数ということになります。

ここで、放物線の凸性に注目します。

xの二乗の係数が0でない場合

下に凸の二次関数 f(x) のとる値は、0 以上の実数値です。

そのため、f(x) = 0 という二次方程式の判別式は 0 以下となります。

つまり、
(Σ_i=1n p_iq_i)²－(Σ_i=1np_i²)(Σ_i=1nq_i²) ≦ 0

移項すると、
(Σ_i=1n p_iq_i)² ≦ (Σ_i=1np_i²)(Σ_i=1nq_i²) となります。

この真ん中に書いている不等式は、f(x) について、二次方程式 f(x) = 0 の判別式です。

今、f(x) は二次関数で、赤色の式に変形する前の段階で、f(x) の値は 0 以上ということが分かっていました。

下に凸の放物線で、とる値が必ず 0 以上だから、判別式は 0 以下となります。

よって、真ん中の不等式が得られ、そこから移項をします。

その後で、両辺にルートをつける、つまり、両辺を 1/2 乗 すると、図の最後に書いている不等式となります。

この最後の不等式が、n 変数のシュワルツの不等式です。

ルートをつけるという無理関数 g について、
0 ≦ a ≦ b だと 0 ≦ g(a) ≦ g(b) となるということを使いました。

これで、有名不等式の証明ができました。この結果を用いて、相関係数の値の範囲を導きます。

相関係数 :r の値の範囲

二つの変量 x と y の大きさを、どちらも自然数 n とします。

そして、x と y の偏差をそれぞれ順に次のように置いておきます。

　a₁, a₂, … , a_n
　b₁, b₂, … , b_n

※ 上の方が x の偏差たちで、下の方が y の偏差たちです。

x と y の共分散を S_xy と表します。また、S_x が x の標準偏差で、S_y が y の標準偏差です。

今回の相関係数の議論の前提として、
S_x ≠ 0, S_y ≠ 0 とします。

相関係数 r の定義は、r = S_xy / S_xS_y です。

標準偏差には、全体にルートがついているので、二乗をした S_x² と S_y² を用いて計算を進めます。

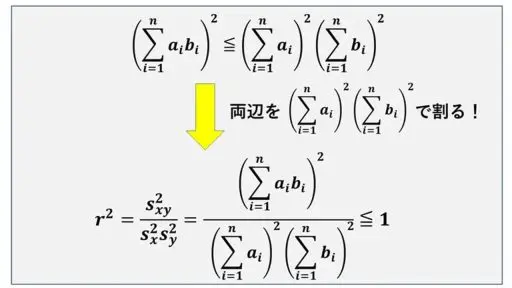
そのため、r² を計算します。

共分散と標準偏差の定義では、1/n がついていますが、r² について、分母と分子のどちらにも 1/n² が出てくるので、それは約分されて 1 となります。

この約分して 1/n² が書かれていないシンプルな形にしたものが、次の図の (1) です。

よって、x と y についての相関係数 r の 二乗の値は次となります。

次の図の (1) 式の右辺の値が 1 以下となることを、シュワルツの不等式から導きます。

シュワルツの不等式の右辺が分母にくるように不等式を同値変形します。

シュワルツの不等式の右辺の値で、シュワルツの不等式の両辺を割ります。

※ S_x ≠ 0, S_y ≠ 0 という前提から、0 でないので割っています。

そうすると、(1) の右辺となります。そのため、値が 1 以下ということになります。

求める範囲へ到達

これで、r² ≦ 1 ということから、この二次不等式を解くと、－1 ≦ r ≦ 1 が得られます。

相関係数 r について、この記事で値の範囲について述べました。

この記事で二次関数について述べました。

これについての基礎内容は、平方完成という記事で解説をしています。

新課程になっても、データの分析は、ますます存在感が大きくなっているようです。

分散という記事では、高一の統計分野を基礎からシンプルな例を用いて解説しています。

また、距離関数という記事でも、今回の記事で証明したシュワルツの不等式を使います。

読んで頂き、ありがとうございました。

これで、今回のブログ記事を終了します。