加速度ベクトル | 速度の公式を微分の観点から【数III】

" 加速度ベクトル “に関連する公式たちを定義から微分を使って導きます。
定義から明確なアルゴリズムで広がりを見せる数学IIIの理論は、物理にも応用が効くので、しっかりと公式の成り立ちを理解しておくと良いかと思います。
平均速度から極限を用いての瞬間の速度を定義するところから、議論が進みます。
速度には向きがあるため、正の向きと反対の向きを表す負(マイナス)の向きも考慮します。
向きを考慮せずに速度の大きさだけに注目すると速さです。
そのため、速度に絶対値をつけると速さです。
まずは一次元である数直線上の点の動きから、速度にまつわる定義から始めます。
加速度ベクトル :位置と時刻の関係
物体の移動を点 P の移動と見なし数学モデルを考えるという発想で、点 P の位置を幾何的に表します。
そうすると、ベクトルを用いて点 P の位置を表すということが効果的となります。
そこで、中学一年のときに数学で学習する数直線というものを詳しく復習しておきます。
長さや面積をもたない点が無限個つながって直線を形成しています。
このままだと、直線上の点が、どの点なのか区別がつかないので、印をつけます。その印は背番号のように実数を使って表します。
点 P(0) だと、原点 0 の位置です。
点 P(4) だと正の向きに原点から距離 4 だけ離れた位置 4 です。
点 P(-4) だと、負の向きに原点から距離 4 だけ離れた位置 -4 です。
マイナスの有無によって方向を判断するわけですが、絶対値をつけると、その実数の位置の原点からの距離となります。
|-4| = 4 なので、-4 の位置は、原点から距離 4 だけ離れているということです。
原点を位置ベクトルの基準として、点 P を p と位置ベクトルで表すこともできます。
これで数直線上を点 P が動いたときに、点 P のいる場所である位置を数学モデルで表すことができました。
ここから、関数(写像)の対応を考えます。
時刻に応じて対応する実数
点 P が数直線上を移動しているとき、ある時刻 t における位置 x を対応させるということで、関数の一対一対応が定義できます。
x = f(t) という関数の対応です。
たとえば、時刻 t = 5 のとき、点 P が数直線上の 9 の位置に居たとします。
このとき、時刻を表す実数 5 に対して、点 P の位置を表す 9 が対応します。
9 = f(5) という対応になります。
この時刻と位置の対応から、速度(速さ)を定義します。
【速度の定義】
時刻 t から Δt だけ時間が進んだとする。
このとき、
点 P が f(t) から f(t+Δt) まで移動したことに対する平均速度を次で定義する。
すなわち、
{f(t+Δt)-f(t)}÷Δt を平均速度とする。
算数で学習した「速さの公式」ですが、中学一年の数学の正負の数を取り入れています。
f(t+Δt)-f(t) の値がマイナスのときは、負の方向へ移動したということになります。
向きまで考慮に入れて平均速度を定義することができました。
ここで気になる内容が出てきます。
点 P の移動速度は、いつも一定とは限らないということです。
まさに、その瞬間の速度というものを数学モデルにおいて定義しておきたいところです。
そうすると、物理などへ数学モデルが適用できます。
加速度ベクトル :瞬間の速度から加速
【時刻 t と位置 x】
x = f(t) が、時刻 t における点 P の位置を表す対応
この対応をベースにして、平均速度を定義しました。
ここからは、瞬間の速度を定義します。
平均速度の定義では、Δt という時間の幅で考えていました。
この時間の幅を限りなく 0 に近づけるという極限操作を行います。
つまり、
{f(t+Δt)-f(t)}÷Δt という Δt の時間の幅で考えた平均速度の式において、Δt → 0 とします。
このときに、
{f(t+Δt)-f(t)}÷Δt が収束した値を時刻 t における瞬間の速度と定義します。
これは、数学IIや数学IIIで学習する微分による導関数の定義です。
そのため、時刻 t における瞬間の速度は、
f'(t) の値ということです。
つまり、
x = f(t) を t で微分したので、
dx/dt = f'(t) です。
この f'(t) を v と置き、
v = f'(t) と表すことにします。
※ 1 次元の数直線上の動きなので、実数値になっていますが、2 次元や 3 次元だとベクトル値で速度ベクトルが定義されます。
|v| は、速さということになります。
さらに加速度を定義します。
坂道を転がる物体のように速さが次第に加速したり、ブレーキを踏んで減速したりすることを表現するために、加速度まで考慮できるようになります。
第二次導関数で加速度
v = dx/dt = f'(t) という瞬間の速度を、さらに t で微分します。
すると、
d2x/dt2 = f"(t) となります。
この x = f(t) の第二次導関数が加速度です。
α = f"(t) と表すことにします。
これで、数直線上の座標 x と時刻 t を対応させることから議論を進めて、速度と加速度を定義することができました。
ここまでの内容をまとめておきます。
【位置と時刻の対応】
x = f(t) が時刻 t における点 P の数直線上の位置
【瞬間の速度の定義】
v = dx/dt = f'(t) が時刻 t における瞬間の速度
【加速度の定義】
α = dx2/dt2 = f"(t) が時刻 t における加速度
向きを考えずに大きさだけを考えるときは、絶対値をつけて表します。
|v| や |α| が、それぞれ瞬間の速度の大きさである速さと、加速度の大きさです。
練習に、物理基礎で学習する内容を数学IIIの内容で考えてみます。
物理基礎を数学IIIで
初速度 100m/s で物体を真上に投げ上げます。
地球の重力の影響で、
1 秒毎に 9.8m/s だけ減速すると物理的に観測されていたという設定で議論を進めます。
物理的な観測内容が正しいとして、上述の数学モデルを適用します。
t = 0 を投げ上げた瞬間の時刻とします。
x = 0 を投げ上げた地上の位置し、そこから垂直方向に上を正の向きとします。
すると、時刻 t における瞬間の速度 v は、物理の内容から次のようになります。
すなわち、
v = dx/dt = 100-9.8t です。
数学モデルを適用しているので、微分と不定積分の内容が使えます。
x を t で微分したものが v の式ですから、その式を t で積分すると元の式へと帰ります。
ただし、積分定数 C のズレが起きるかもしれないので、ここを詰める必要があります。
dx/dt = 100-9.8t を t で積分します。
dx/dt は、微分積分学の基本定理から x にもどります。
∫(100-9.8t) dt
= 100t-4.9t2+C です。
このため、
x = 100t-4.9t2+C となります。
ここで、t = 0 のとき、物体が地上にあるので x = 0 という設定を使います。
x と t に 0 を代入すると、
0 = 0-0+C となります。
これで、C = 0 なので、
x = 100t-4.9t2 という等式が導かれました。
時刻 t と位置 x の関係が、はじめは与えられていませんでしたが、数学の理論の適用から x を t を用いて関数として表すことができました。
x = f(t) = 100t-4.9t2 です。
x = f(t) は二次関数なので、横軸を t 軸、縦軸を x 軸としてグラフを描いて、具体的な値をグラフから考察することもできます。
この内容は、1 次元である数直線を移動する点についての数学モデルを、球を投げ上げるという 3 次元の具体的な形而下の世界へ適用しました。
より考察するバリエーションを増やすために、2 次元の数学モデルも考えたいところです。
今度は、平面上を動く点についての数学モデルを構築します。
ベクトル値関数といって、時刻を表す実数 t に対して、平面ベクトルを対応させるということを考えます。
※ 内積の定義という記事で平面ベクトルについての基礎的な内容を解説しています。
しかし、同じ操作を単に繰り返すだけだと壁があります。
xy-座標平面上の点 P(x, y) について、位置は座標で表せますが、座標をどうやって微分して速度とするのかという壁を越える必要があります。
そこで、成分を切り分けて考え、議論を進めます。
加速度ベクトル :平面上だと射影を利用
点 P(x, y) が xy-座標平面上を動くとします。
(x, y) という座標が時刻 t における点 P の位置を表します。
先ほどは、1 次元の数直線上の点の移動について、瞬間の速度や加速度を定義しました。
1 次元なので、ベクトルの記号を使わずに実数だけで議論を進めることができましたが、平面上を動くときは、点 P を位置ベクトルで表して議論を進めます。
p = (x, y) は、原点 (0, 0) を始点に、点 P を終点にした位置ベクトルです。
x が x 成分の値で、y が y 成分の値です。
このベクトルを射影を用いて二つに分解します。
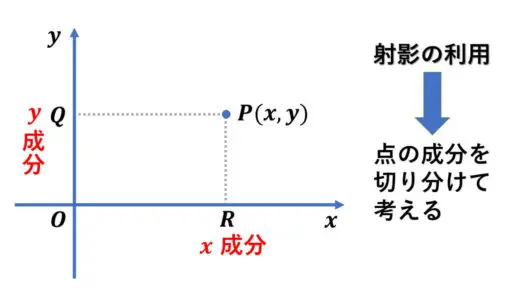
点 P から x 軸へ垂線を引き、その交点を R とします。
この点 R の x 座標の値を、点 P から x 軸への射影による像といいます。
※ プロジェクションというnote記事で射影について例を用いて解説をしています。
そして、点 P から y 軸へ垂線を引き、その交点を Q とします。
点 Q の y 座標の値を、点 P から y 軸への射影による像といいます。
たとえば、P(2, 3) だと、
R(2, 0) なので、x 成分への射影による像は 2 という値になります。
Q(0, 3) については、3 が y 成分への射影による像です。
このように射影を使って点 P の成分を分けておくと、時刻の変化にともなって点 P が移動したときに、点 R と点 Q がついてきます。
このことを使って、時刻 t についての関数を二つ定義します。
時刻 t における点 P の位置が (x, y) のとき、t に対して、点 P の x 成分の値を対応させる関数を f とします。
また、t に対して、点 P の y 成分の値を対応させる関数を g とします。
つまり、
x = f(t), y = g(t) という関数です。
点 R と点 Q は、1 次元の数直線上を移動することになるので、点 R と点 Q については、上述の瞬間の速度や加速度の定義が使えます。
dx/dt = f'(t) は、時刻 t における点 R の瞬間の速度です。
また、dy/dt = g'(t) が、時刻 t における点 Q の瞬間の速度です。
さらに、第二導関数を使うことで、それぞれの加速度も定義されています。
f"(t) と g"(t) が、それぞれ点 R と点 Q の時刻 t における加速度です。
これらのパーツを使って、点 P の瞬間の速度や加速度を表すベクトルを構成します。
ベクトルの加法で和をとることが決め手になります。
ベクトルの和で合わせる
点 P(x, y) を座標平面上の点 P の時刻 t における位置とします。
p = (x, y) という平面ベクトルは、x 成分と y 成分の射影を使って分解することができます。
点 R と点 Q の位置ベクトルをそれぞれ r, q と表すことにします。
r = (x, 0), q = (0, y) です。
そのため、ベクトルの和をとると、
p = (x, y) = r + q となります。
x = f(t), y = g(t) という時刻 t についての関数も使えます。
p = (x, y) = (f(t), g(t)) です。
これが、
時刻 t という実数に対し、
(f(t), g(t)) というベクトルを対応させるベクトル値関数です。
このベクトルを値として対応させる関数を φ と表すことにします。
すると、
φ(t) = (f(t), g(t)) が時刻 t における点 P の座標平面上での位置ということになります。
射影で数直線上に落とされた影である点 R と点 Q については、瞬間の速度と加速度が既に定義できています。
r と q の和で点 P の座標が復元できるということから、座標平面上を動く点 P の瞬間の速度と加速度を定義します。
(f'(t), 0) + (0, g'(t))
= (f'(t), g'(t)) です。
この (f'(t), g'(t)) が、φ(t) を t で微分した導関数 φ'(t) です。
φ'(t) = (f'(t), g'(t)) を時刻 t における点 P の速度ベクトルと定義します。
この流れで、φ の第二導関数も考えることができます。
φ"(t) = (f"(t), g"(t)) を時刻 t における点 P の加速度ベクトルと定義します。
これで、射影を用いて座標平面上を動く点に関する速度ベクトルと加速度ベクトルを定義することができました。
ちなみに空間内を動く点についても、射影を用いて速度ベクトルと加速度ベクトルを定義することができます。
空間内を動く点に関して
P(x, y, z) を空間内を動く点だとします。
時刻 t における位置を射影を用いて表しておきます。
x 軸、y 軸、z 軸の上に射影をして、x, y, z を t を用いて表します。
x = f(t), y = g(t),
z = h(t) としておき、
(f'(t), g'(t), h'(t)) を点 P の時刻 t における速度ベクトルとします。
同じく第二導関数まで考えて、
(f"(t), g"(t), h"(t)) を加速度ベクトルとします。
こういった微分と速度についての理論の応用として等速円運動という記事、そして、置換積分という数学IIIの積分の内容も投稿しています。
物理基礎の内容については、運動方程式という記事を投稿しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。