イデアル 積 | 環のイデアルの積について【後半で3年次の内容にも】
" イデアル “は環論の入門的な学習を始めるときに、基本となります。
環のイデアルの定義から議論をスタートし、イデアルの積について解説します。
また、代数学の専門課程で数学科の3年くらいで扱うイデアルの内容についても解説をします。
環 R が非可換のときは、左イデアルと右イデアルを区別します。
イデアルの定義から順に説明を進めます。
イデアル :環のイデアルの定義から
【定義】
環 R の部分集合 A が次を満たすとき、A を R の左イデアルという。
[1] 和で閉じている
a, b∈A に対し、a+b∈A
[2] 左作用で閉じている
a∈A, r∈R に対し、ra∈A
環 R から R 自身への作用(アクション)を R において定義されている積で定義します。
そのとき、[2] は、左から a に r を乗じているという内容になります。
行列環のように、R の乗法が可換とは限らないときには、ra が A の元だからといって、ar も A の元とは限りません。
そのため、R が可換環とは限らないときには、[2] を左イデアルの条件として、右イデアルと区別します。
[1] の和で閉じているということは、右イデアルについても同じ条件で定義されます。
しかし、R が非可換なときは左イデアルと区別し、[2] のかわりに次の [3] を定義とします。
[3] 右作用で閉じている
a∈A, r∈R に対し、ar∈A
[1] と [3] の条件をともに満たすときに、右イデアルといいます。
A ⊂ R が、左イデアルであり、なおかつ右イデアルとなっているときもあります。
即ち、[1], [2], [3] をすべて満たすときには、両側イデアルといいます。
部分環との違い(加群)
K ⊂ R が部分環であるかどうかを判断するときに、R における和と積で閉じているかどうかを確認します。
この積は、K × K → K となっていることを見るため、K の元どうしの積で考えます。
それに対して、A が R の左イデアルかどうかの [2] で確認する内容は、R との元との積で考えています。
R × A → A となっているかどうかを確認するわけです。
そのため、R-A という差集合の元 r と A の元 a の積が A の元となっていることも示さなければなりません。
R の元を左から掛けるという作用で閉じているという条件が [2] です。
[1] と [2] をともに満たすということは、左イデアル A が左R-加群であるということになります。
右から R の元を乗じるという作用について、[1], [3] を満たすとき、即ち、右イデアル A が右R-加群です。
[1], [2], [3] をすべて満たす両側イデアル A は、両側R-加群です。
一方、部分環については、A の元どうしの積しか考えていません。
※ 加群の定義などの基礎的な内容は、リンク先の記事で解説をしています。
部分環とイデアルの違いを定義の段階から押さえておくと、後々の環論の学習が円滑かと思います。
ここからは、イデアルの和と積について、解説します。
まずは、シンプルな和の方から説明し、積の方へと議論を進めます。
イデアル :イデアルどうしの積
A, B を環 R の左イデアルとします。
このとき、
{a+b | a∈A, b∈B} = A+B と表すことにします。
A+B も R に左イデアルになります。
条件 [1] を確認します。
a, c ∈A, b, d ∈B に対し、
(a+b)+(c+d)
= (a+c)+(b+d)
ここで、
a+c ∈A, b+d ∈B より、
(a+c)+(b+d) ∈A+B
即ち、
(a+b)+(c+d) ∈A+B です。
これで、左イデアルの条件 [1] が確認できました。
R における加法の結合律と交換律が効きました。
次に、条件 [2] を確認します。
a ∈A, b ∈B, r ∈R とします。
このとき、
r(a+b) = ra+rb です。
左イデアルの定義から、
ra ∈A, rb ∈B なので、
ra+rb ∈A+B です。
即ち、
r(a+b) ∈A+B です。
これで、条件 [2] も確認できました。
R における分配律が効果を発揮しました。
A, B が右イデアルのときは、条件 [3] を確認するときに、右から R の元を乗じるときに、同じく分配律を使うことで証明ができます。
そのため、A と B が R の両側イデアルであるとき、A+B も R の両側イデアルとなります。
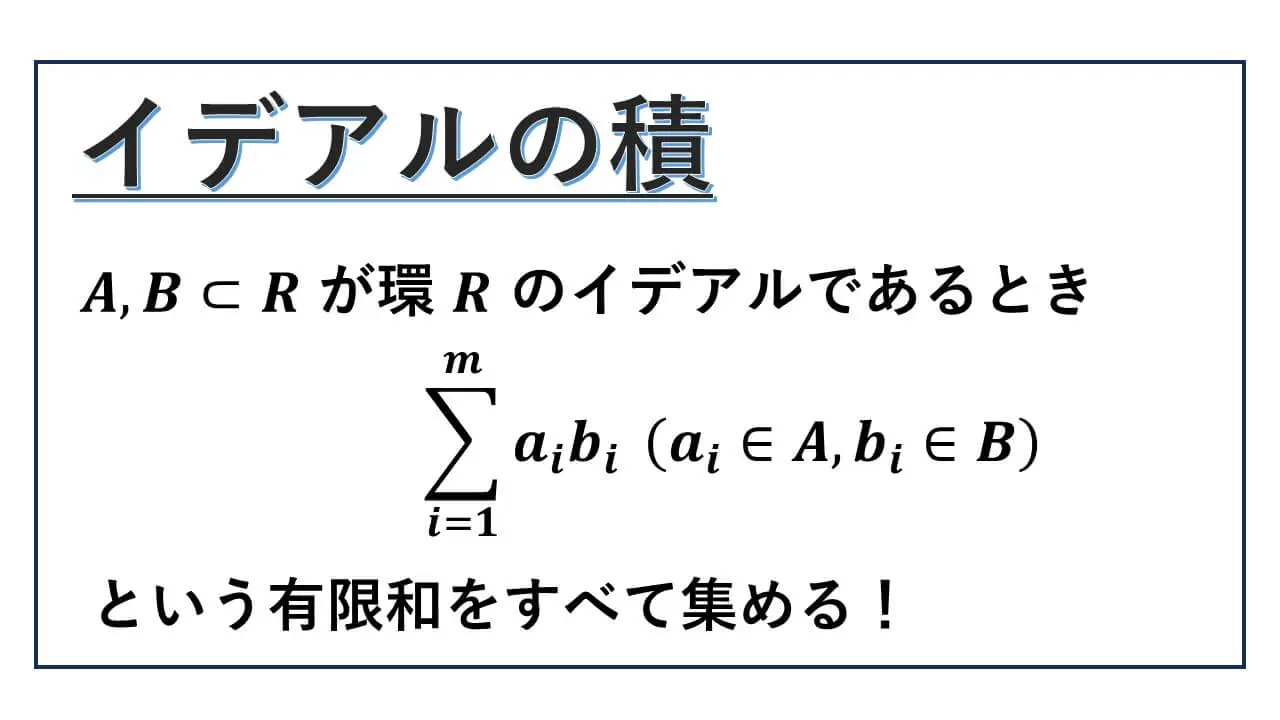
それでは、イデアルの積について説明します。
有限和どうしの和は有限和
{Σi aibi | ai∈A, bi∈B} を AB と表すことにします。
ただし、Σi aibi は有限和とします。
すなわち、A の元と B の元の積を有限個で加法をとったものをすべて集めたものが AB です。
A と B が R の左イデアルのとき、AB も R の左イデアルとなります。
まずは、条件 [2] から確認します。
Σi aibi (ai∈A, bi∈B) に、左から R の元 r を掛けます。
r(Σi aibi) = Σi r(aibi)
= Σi (rai)bi です。
左イデアルの定義から、
rai ∈A です。
そのため、
Σi (rai)bi は、A の元と B の元の積を有限個で加法をとったものです。
即ち、r(Σi aibi)∈AB です。
これで、条件 [2] が確認できました。
次に条件 [1] を確認します。

有限個は有限個です。
m 個と n 個なので、
(m+n) 個の A の元と B の元の積の和です。
そのため、
(Σi aibi)+(Σj cjdj) ∈AB が示せました。
A, B が R の右イデアルのときや、両側イデアルであるときも、[1] が同様に示せ、[2] の証明は同じです。
即ち、A, B が R の右(両側)イデアルのとき、AB も R の右(両側)イデアルとなります。
ここから、3年次くらいに扱われるイデアルに関連する内容について述べておきます。
3年のときくらいに扱う内容
【定理】
単項イデアル整域ならば素元分解整域である。
一意分解整域という記事の最後で述べていた定理の証明になります。
<証明>
背理法で示します。
もし単項イデアル整域 R において、0 でも単元でもない元で、素元の積に分解しない a ∈ R が存在したとします。
a が素元だと、a = 1a と素元分解されていることになるので、この a は素元ではありません。
Ra = R とすると、ある r ∈ R が存在して、
ra = 1 となり、a が単元でないことに反します。
よって、Ra ≠ R となっています。
一意分解整域という記事で示した【命題2】より、
Ra を含む R と異なる R のイデアルの中で、
極大なイデアル N1 が存在し、
Ra ⊂ N1
今、R が単項イデアル整域なので、N1 が一元で生成されています。その N1 の生成元を b1 とします。
Rb1 = N1 ≠ R なので、b1 は単元ではありません。(b1 が単元だとすると、Rb1 の中に 1 が含まれてしまい、N1 が R と異なることに反します。)
また a が 0 でないため、b1 も 0 ではありません。
a ∈ N1 = Rb1 より、ある c1 ∈ R が存在して、
a = c1b1 … (1)
今、単項イデアル整域において、a が素元でないので、a は既約元ではありません。
c1 が単元だとすると、a1 が単元ではないので、(1) から、a が既約元ということになってしまいます。a は既約元でないため、c1 は単元ではないということになります。
また、(1) から a が 0 でないため、c も 0 ではありません。
(1) と先ほどの記事の【命題1】より、
Rb1 と Rc1 は、どちらも Ra を真に含む R と異なるイデアルです。
b1 と c1 の両方ともが素元の積に分解したとすると、(1) から a が素元の積に分解することになってしまいます。
そのため、b1 か c1 のうち、少なくともいずれか一方は素元の積に分解しないことになります。
その素元の積に分解しない方を a1 と置きます。(どちらも素元分解されていないときは、どちらを a1 としてもかまいません。)
Ra ⊂ Ra1 で、Ra1 は真に Ra を含んでいて、a1 は素元の積に分解しない 0 でも単元でもない元という状況です。
ここまでの議論を繰り返すことで、
Ra ⊂ Ra1 ⊂ Ra2 ⊂ … という上昇列が作られます。
各 ak について、Rak は Rak+1 に真に含まれていて、ak たちは素元の積に分解しない 0 でも単元でもない元です。
ここで、A = ∪kRak と、上昇列に現れたイデアルたちの和集合をとります。
A は R のイデアルとなっていることが分かります。イデアルになっていることの確認は、後で述べることにします。
R が単項イデアル整域であることから、A は一元で生成されています。その生成元を x と置くことにします。
つまり、Rx = A = ∪kRak です。
x ∈ A なので、和集合の定義から、ある自然数 t が存在して、x ∈ Rat
よって、
Rx ⊂ R(Rat) = (RR)at ⊂ Rat
一方、Rx = A ⊃ Rat だから、
A = Rx = Rat
上昇列の作り方から、Rat+1 は Rat を真に含んでいるため、
A = ∪kRak ⊂ Rat+1 と Rat+1 が 和集合 A を真に含むことになります。
これは、矛盾です。
よって、背理法から、単項イデアル整域 R において、0 でも単元でもない元で、素元の積に分解しない a ∈ R が存在しないことが示せました。【証明完了】
念のために確認
今の証明で、A = ∪kRak がイデアルであることを使いました。
包含関係についての極大なイデアルのときに、同じような状況でイデアルとしていたので、念のために確認しておきます。
y ∈ A = ∪kRak, r ∈ R とします。
和集合の定義から、
ある自然数 s が存在し、y ∈ Ras
よって、
ry ∈ r(Ras) = (rR)as ⊂ Ras
また、y, z ∈ ∪kRak とすると、ある自然数 s, s’ が存在して、y ∈ Ras, z ∈ Ras’
s ≦ s’ の場合は、y, z ∈ Ras’ より、
y + z ∈ Ras’ ⊂ A
s’ ≦ s の場合は、y, z ∈ Ras より、
y + z ∈ Ras ⊂ A
いずれの場合にも、y + z ∈ A となっています。
これで、A がイデアルであることを確認できました。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。