判別式 | 三次方程式で考える【自分で既にある内容から踏み出す一歩】

" 判別式 " を二次方程式について、高校のときに学習します。この判別式を三次方程式(三次の多項式)について考えます。
環論や体論の入門的な内容で扱われる話ですが、大学の数学科の後半、体論を学習することもあるかと思います。
大学の三年生も終わりに近づいてくると、自分で考えたことを発表するときもあるかと思います。
そんなときに、地道な計算式の観察も大切になるかもしれません。
まずは、高校で学習する二次方程式についての判別式の復習から説明を始めます。
そして、大学数学の計算データの観察の部分について、地道な積み重ねから道が開ける雰囲気を述べています。
二次方程式の判別式を復習し、三次の判別式へ向かうという流れです。
判別式 :二次方程式から三次へ向けて
ax2 + bx + c = 0 (a ≠ 0) という二次方程式についての判別式を高校一年のときに学習します。
a, b, c はそれぞれ実数で、二次の方程式なので、最高次係数 a は 0ではないとしています。
この二次方程式の解の公式のルートの中に現れている b2 – 4ac が二次方程式の判別式です。
この値が 0 になっていると、解の公式のルートの部分が 0 になっているので、二次方程式が重解をもつと判断できました。
この重解をもつかどうかの判定に使われる式が判別式です。
そして、二次方程式の解を α と β とすると、因数定理から、方程式に使われている二次の多項式を次のように分解して、解と係数の関係が得られました。
ax2 + bx + c = a(x – α)(x – β)
よって、
α + β = – b/a, αβ = c/a という解と係数の関係が得られます。
※ 2 変数の高校数学の解と係数の関係については、高校数学の内容の詳細をリンク先で解説しています。
これらの等式を判別式に代入すると、次のような形になります。
b2 – 4ac
= {a(α + β)}2 – 4a(aαβ)
= a2{(α + β)2 – 4 αβ}
= a2(α2 – 2αβ + β2)
= a2(α – β)2
大学の数学で扱う形に判別式を書き換えました。
この三次方程式版をこれから解説します。
実は、一般に n 次の多項式についての判別式についての定理が、終結式やシルヴェスターの行列式を用いて証明されています。
ただ、自分から発表するということを考えたときに、そのような複雑なものを自力で考えつくのは、一部の方を除いて困難かと思います。
そこで、ちょっとした参考に、私の卒論の経験談を述べてみようと思います。
ちょうど三次の多項式についての判別式を使う場面が、体論を学習する頃かと思います。
数学科の後半の内容なだけに、何かの参考になれば幸いです。
三次方程式において
卒論を書こうとしたときに、既に成立している内容から、わずかでも前進をする必要が出てきます。
もちろん、学部の卒論ですから、専門家の高度な論文に遠く及ばないものになるのが普通かと思います。
それでも、既にある内容から、わずかでも前進しようとすると、困難なものに。
私の卒論は、単なるお話程度のものでしたが、自分で踏み出す一歩は、大変だったと記憶しています。
そのときの経験ですが、自分の足で動くために、「自分独自の情報を持つ」ということから、行動へつなげようとした記憶があります。
そして、既にある内容の定義や条件を変更して、自分独自のもつ情報と合わせて、ちょっとしたことを卒論として発表したわけです。
私の卒論は判別式ではないのですが、三次の判別式は、自分独自の情報を得るということについて、いくばくかの経験や雰囲気を伝えられればと、今回のブログ記事で取り挙げました。
x3 + cx + d = 0 の判別式は、
-4c3 -27d2 となります。
これは、環論の入門もしくは体論の入門の中で扱われるかと思います。
千年くらい前の数学者になったつもりで、この内容から前進することを考えてみます。
x2 の係数が 0 という状況で、練習問題のような形で学習するかと思います。この x2 が 0 という部分を拡張して、
ax3 + bx2 + cx + d = 0(ただし、a ≠ 0)の判別式を求めることを考えます。
この三次方程式の根を α、β、γ とします。
与えられた係数とつなげる
a ≠ 0 なので、分母に a を置けるので、方程式の両辺を a で割って、最高次係数を 1 とします。
すなわち、
x3 + (b/a)x2 + (c/a)x + d/a = 0
ここで、
左辺の三次多項式について、因数定理を適用すると、(x – α)(x – β)(x – γ) = 0
この左辺を展開して、係数を比較することで、次の解と係数の関係が得られます。
α + β + γ = – b/a,
αβ + βγ + γα = c/a,
αβγ = – d/a
これらの三次の基本対称式の値を使って、先ほどの -4c3 -27d2 の判別式よりも前進することを試みます。
Δ = (α – β)(α – γ)(β – γ) の二乗と、与えられた三次方程式の係数 a, b, c, d をつなげたいわけです。
「自分独自の情報」というのが、卒論らしい部分になってきます。
それを得るための 1 つの手として、多くの方が、行動に移しにくい所を探ってみるのも良いかと思います。
私の卒論の場合だと、手間をかけて、図書館の本などに載っていない内容を手に入れた記憶があります。
どのようなときに、多くの方が行動に移しづらくなるのかということの参考になりそうなのが、この三次の判別式です。
Δ = (α – β)(α – γ)(β – γ) の二乗を展開してみます。
数か月などの時間で考える

これくらいに計算量を増やすと、行動が起きにくいはずです。多くの人が調べていなさそうなところを探ってみます。
受験のときだと、これくらいの量の計算になると、やり方が間違っている感じがします。
ところが、時間制限が 1 時間以内というようなことを無くすと、これくらいの計算量だと、ほどよく時間をかけて考察できます。
これらの式を基本対称式で表すことができると、Δ の二乗と、与えられた三次方程式の係数 a, b, c, d を結びつけることができます。
この三変数多項式について、いろいろと試してみます。1 週間、1 月と計算をひたすら続けてみるわけです。
上の図で、赤色や青色で書いている部分は目立つので、この形を意識して、計算をすることにします。これくらいの時間を使えば、何か得られるかもしれません。
研究の感じが少ししてきましたでしょうか。千年前の研究者になったつもりで、この数学的対象を調べてみます。
※ このブログ記事を書くにあたって、何日か無理なく時間のあるときに計算して辿り着いたものになります。
判別式 :独自データを得るために

基本対称式の二乗や三乗を交えて、それらしい等式が出てきました。
色をつけていた部分に、少しかすっているものが得られました。
こういうのが出てくると、粘ってみようかと思えます。
理系の実験データのようなものです。効果的な良いデータを集める意識で頑張ります。
ちなみに、x1px2qx3r について、p + q + r を総次数 (total degree) といいます。
どの項も同じ総次数になっているときに、斉次多項式といいます。
α、β、γ で 3 変数の多項式と思うと、どの項も 6 次になっています。
こういうことも考えて、赤色と青色の目印をつけました。
2 + 2 + 2 という目立つ項が赤色です。0 乗が 1 つ出て 2 変数となっている項を青色としています。
計算をするときに、目指す目標として、赤色と青色を意識します。さらに計算を進めます。
まとまりを合計してみる
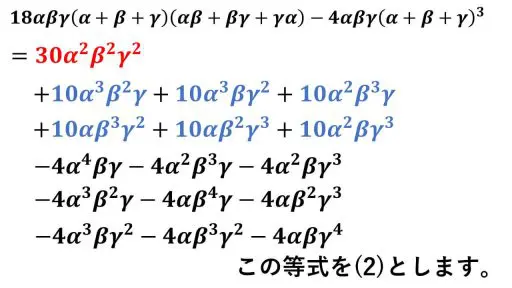
実験データをいろいろと調べていると、関連し合うものがあるかもしれません。
そういえば、計算をし始めた頃に、青色をつける基準を違うものにしていたなと、ふと気になりました。
よく見ると、(1) の等式と同じ項が出ています。あきらめかけていたときに、糸口が見え始めることもあるかもしれません。
(1) + (2) を計算すると、次のようになります。
21α2β2γ2+α4β2-2α3β3+α2β4+β4γ2-2β3γ2+α4γ2-2α3γ3+α2γ4+β2γ4-2αβγ4-2αβ4γ-2α4βγ+2αβ2γ3+2αβ3γ2+2α3β2γ+2αβ2γ+2α2βγ3+2α3βγ2
後は -6α2β2γ2 との違いを調整です。
Δ2 = (α – β)2(α – γ)2(β – γ)2 を展開した等式★との違いは、赤色の α2β2γ2 の係数だけです。
-27α2β2γ2 を加えると、同じ式になります。
こんな感じで、独自の情報を得られると、自分独自の発表への足掛かりになるかもしれません。
式をまとめます
Δ2 = (α – β)2(α – γ)2(β – γ)2 は次のようになります。
Δ2 = (αβ + βγ + γα)2(α + β + γ)2
– 4(αβ + βγ + γα)3
+ 18αβγ(α + β + γ)(αβ + βγ + γα)
– 4αβγ(α + β + γ)3– 27α2β2γ2
では、三次の解と係数の関係をこれに当てはめます。
α + β + γ = – b/a,
αβ + βγ + γα = c/a,
αβγ = – d/a
でした。
Δ2 = (c2b2)/a4 – (4c3)/a3
+ (18bcd)/a3 – (4b3d)/a3
– (27d2)/a2
両辺に a4 を掛けると、次のようになります。
a4Δ2 =
c2b2 – 4ac3 + 18abcd – 4ab3d – 27a2d2
結果に辿り着きました。
ただし、結果が得られても、それが何の意味があるのかを伝えられないものだと、聞き手に受け入れられないかもしれません。
論理的に意味があるものということを説明できるものかどうかを検討することも大切になります。
判別式 :重解を判定する
Δ = (α – β)(α – γ)(β – γ) には、与えられた三次方程式の三つの解(根)が使われています。
もし重解があれば、Δ = 0 となります。
逆に Δ = 0 のとき、α、β、γ を体の元という設定にしておくと、体は整域ですから、
α – β = 0 または α – γ = 0 または β – γ = 0 となり、重解をもつということになります。
したがって、Δ = 0 が与えられた三次方程式が重解をもつことの必要十分条件です。
そして、a が 0 でないということから、
Δ = 0 と a4Δ2 = 0 は同値です。
このことから、与えられた三次方程式の係数から、a4Δ2 を計算することで、その三次方程式が重解をもつかどうかを判別できる式を構成できたということになります。
x3 + cx + d = 0 の判別式 – 4c3 -27d2 は、今、求めた判別式に b = 0 を代入したものと一致しています。
b が 0 でないときについても、判別式が求められたので、練習問題から前進したことになります。
千年くらい前の内容を用いて、自分独自の発表をする雰囲気を述べてきました。
ギャップを乗り越えて、独自の情報を得ることができると、チャンスがあるかもしれませんという話でした。
そのことと、定義や条件を変更して調べてみるということを合わせることも重要かと思います。
例えば、5 次方程式には解の公式が存在しないということがアーベルによって証明されています。
これは、解の公式とはどういったものかということを定義した上で、存在しないということをアーベルは証明したものです。
実際、解の公式の定義を変更して、解を構築することが行われました。
こんな感じで、既にある定義や条件を変化させて、少しの一歩が踏み出せないかと考えるのも手です。
そうそううまくいかないかと思いますが、今回のブログ記事で、いろいろと粘り強く試してみた当時の自分の経験のようなものを述べてみました。
重解に関連するブログ記事
今回のブログ記事で、ギャップを乗り越えるという雰囲気を、少し出せればと思い、長い計算をしました。
重根-形式的な微分というリンク先のブログ記事で、多項式が重解(重根)をもつための必要十分条件を、形式的な微分を使って解説しています。
三次の多項式については、微分を使って重解(重根)を判定する方が楽かと思います。
状況に応じて、適した内容で、重根をもつかどうかを言い換えることが大切になります。
また、重根をもたない 3 次の多項式を例に多項式のガロア群について解説をしています。
それでは、これで今回のブログ記事を終了します。
読んで頂き、ありがとうございました。