解と係数の関係 | 中学の頃に学習した内容から大学受験のn乗和まで

2022年6月22日

「 解と係数の関係 」は数学のテストでよく出題されます。正解しやすい問題も多いので、学習したことがテストの得点につながりやすいので良いかと思います。

いつ習うかというと、公立だと中学三年生のときになります。

この記事では、中学で学習しそうな基本的な内容から始めて、高校の定期考査で出るような問題をカバーできるように解説をしています。

また、受験を見据えた技巧的な式の書き換えについても述べています。

それでは、まずは中学の数学で出てくる内容から解と係数の関係について説明します。

解と係数の関係 いつ習う :押さえるべき公式

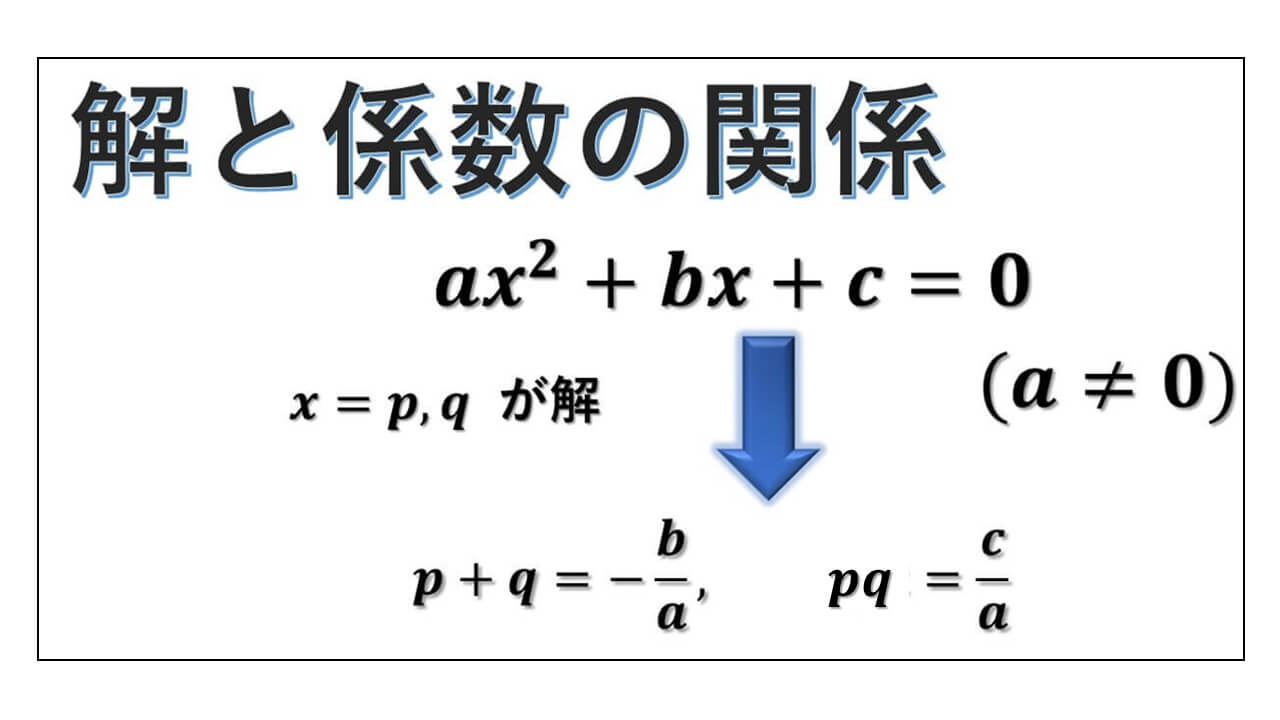
二次方程式の二つの解 α と β の和、積の値について、★の関係が成り立ちます。このことを利用して計算を進める問題が、中学の数学から出てきます。

α + β と αβ の値について、x² の係数 a で割っておくことが必要になります。割り切れないときには、公式★のように分数で表します。

※ 平方完成という記事で、解の公式を導いています。

具体的な数字を使って、練習問題で経験を積んでおくと、得点の UP につながるかと思います。

公式★の練習問題

x についての二次方程式 2x² + bx + c = 0 の二つの解が x = 4, 6 のときに、b と c の値を求めてください。

では、この問題について解説をしていきます。

x² の係数が 2 で、二つの解 α と β がそれぞれ 4 と 6 という状況です。

まず、★に当てはめて等式を作ると、
4 + 6 = －b ÷ 2,
4 × 6 = c ÷ 2 となります。

それぞれの等式とも、両辺に 2 を乗じて分母を払い、
2 × 10 = －b, 2 × 24 = c

よって、b = －20, c = 48

これで答えが求まりました。

解と係数の関係 :高校の定期考査レベル

x + y = 3, xy = 2 のとき、
x⁶ + y⁶ の値を求めてください。

先ほどの解と係数の関係で、和と積の値を使って、議論を進めました。

その考え方と、高校で学習する計算公式の合わせ技で計算ができます。使うのは、次の公式です。

三乗和の因数分解公式
a³ + b³ = (a + b)(a² － ab + b²)

ブログ三乗和の公式より

この公式を使うために、a = x², b = y² と置き換えます。

つまり、x⁶ + y⁶ = a³ + b³

置き換えた右辺に三乗和の公式を使うと、
x⁶ + y⁶
= (a + b)(a² － ab + b²)

a² － ab + b² = (a + b)² － 3ab なので、
a と b をもとに戻すと、
x⁶ + y⁶
= (x² + y²){(x² + y²)² － 3(xy)²}

xy = 2 という設定だったので、
3(xy)² = 3 × 2² = 12 です。

後は x² + y² の値が分かれば 6 乗和が計算できます。

焦点を絞って攻略

x² + y² = (x + y)² － 2xy

x + y = 3, xy = 2 なので、
x² + y² = 3² － 2 × 2
= 9 － 4 = 5

これで、6 乗和が計算できます。

最終的な答えへ

x⁶ + y⁶
= (x² + y²){(x² + y²)² － 12}
= 5 × (5² － 12)
= 5 × 13 = 65

これで、答えが求まりました。

段階を踏んで、到達したいところまで辿り着くことは大切かと思います。

このブログ記事では、和と積の値に注目しています。

※ 数学２の和積変換公式だと、よく似た名前ですが、三角関数の角の値について和と差に関連して議論を進めます。
　
ここから、受験レベルの問題を解説します。

解と係数の関係 :受験レベルの問題に挑戦

二次方程式 2x² －4x + 8 = 0 の二つの解を p, q とします。

このとき、p⁴ + q⁴ の値を求めてください。

【解答と解説】

二解が p と q とギリシャ文字でなくアルファベットになっていますが、気にせずに解と係数の関係を使って、二つの等式を作ってから議論を進めていきます。

p + q = －(－4) ÷ 2 =2,
pq = 8 ÷ 2 = 4

和が －2 で積が 4 です。4 乗和を求めるときには、次のように考えます。

p⁴ + q⁴ = (p² + q²)² － 2(pq)²…■

目指す内容を確認

解と係数の関係から、pq = 4 と分かっているので、p² + q² の値が分かれば、四乗和の値が計算できます。

二乗和が、答えに辿り着くために、目指す内容です。
p² + q²
= (p + q)² － 2pq
= 2² － 2 × 4 = －4

これで四乗和の等式■に、二乗和と積の値を代入すると答えに辿り着きます。

p⁴ + q⁴ = (－4)² － 2 × 4²
= 16 － 32 = －16

これで、答えが求まりました。

二乗和や三乗和について言及されずに、いきなり四乗和の値を問われることもあるので、落ち着いて自分で必要な部分を順に求めることが大切になります。
　
練習に三乗和 p³ + q³ も求めてみます。

p³ + q³
= (p + q)(p² － pq + q²)
= (p + q)(p² + q² － pq)
= 2 × (－4 － 4) = －16

さらに、指数を大きくしたものを考えます。

五乗和から向こうへ

四乗和の値が －16 と分かりました。さらに五乗和や、それ以上について、次のようにして求めることができます。

(p + q)(p⁴ + q⁴)
= p⁵ + pq⁴ + p⁴q + q⁵
= p⁵ + q⁵ + pq(p³ + q³)

p + q = 2, pq = 4, p⁴ + q⁴ = －16,
p³ + q³ = －16 と既に求めているので、等式に当てはめます。

2 × (－16)
= p⁵ + q⁵ + 4 × (－16)
= p⁵ + q⁵ － 64

よって、
p⁵ + q⁵ = －32 + 64 = 32

これで、五乗和の値が求まりました。

一般に、k 乗和の値が分かると、このように k 乗和に (p + q) を掛けることによって、(k + 1) 乗和を含んだ等式を得ることができます。

そのため、k 乗和の値から、(k + 1) 乗和の値を求めることができます。

解と係数の関係 :難関大学レベル

p + q = 6, pq = 8 のとき、
自然数 n に対して、
pⁿ + qⁿ の値を求めてください。

【解答と解説】

和が 6 で積が 8 という状況から議論をスタートします。自然数 n に対して、
f(n) = pⁿ + qⁿ と置きます。

f(n) は自然数 n に対して実数を対応させる関数となっています。

n = 1 と n = 2 について、それぞれどんな実数が対応してくるのかを求めておきます。
　
f(1) = p + q = 6 は問題文の設定そのままの値です。f(2) の値は、二乗和の値なので、ここまで述べてきた求め方で計算ができます。

f(2) = p² + q²
= (p + q)² － 2pq
= 6² － 2 × 8 = 20

f(1) = 6, f(2) = 20 は今後に必要になります。
※ 専門用語で初期値といいます。
　
ここから、自然数 n, n + 1, n + 2 という連続する三つについて成立する関係式を求めます。

(p + q)f(n + 1)
= (p + q)(pⁿ⁺¹ + qⁿ⁺¹)
= pⁿ⁺² + pqⁿ⁺¹ + qpⁿ⁺¹ + qⁿ⁺²
= (pⁿ⁺² + qⁿ⁺²) + pq(pⁿ + qⁿ)
= f(n + 1) + pqf(n)

ここで、p + q = 6, pq = 8 だったので、
6f(n + 1) = f(n + 2) + 8f(n)

つまり、
f(n + 2) － 6f(n + 1) + 8f(n) = 0

この等式（関係式）から、f(n) を n の式で表すことができます。

ここからの考察が長いので、結論を書いておきます。

f(n) = pⁿ + qⁿ = 4ⁿ + 2ⁿ となります。
　
ここからは、どうしてこのようになるのかを説明します。解と係数の関係を使っています。

和が 6 で積が 8 なので、p と q は次の二次方程式の解ということになります。

x² －6x + 8 = 0 を、
(x － p)(x － q) = 0 に書き換えます。

下の二次方程式を展開すると、
和 p + q = 6, 積 pq = 8 から上の二次方程式となるというわけです。

このため、p と q は上の二次方程式の実数解ということになります。
　
x² －6x + 8 = (x － 2)(x － 4) = 0 なので、
x = 2 または x = 4

p は 2 か 4 で、q はもう一方の値ということですが、そこまで決定をする必要はありません。ただ、次のように考えることが重要になります。

p + q = 6 = 2 + 4,
pq = 8 = 2 × 4 です。

f(n+2) － 6f(n+1) + 8f(n) = 0 という先ほどの等式の 6 を (2 + 4) に、8 を 2 × 4 に書き換えます。

f(n+2)－(2+4)f(n+1)+2 × 4 × f(n) = 0 を移項して整理します。

f(n + 2) － 2f(n + 1)
= 4f(n + 1) － 4 × 2 × f(n)

よって、
f(n + 2) － 2f(n + 1)
= 4{f(n + 1) － 2f(n)} … ★

今度は、6 = 4 + 2, 8 = 4 × 2 と考えて、同様に等式を書き換えます。

f(n + 2) － 4f(n + 1)
= 2{f(n + 1) － 4f(n)} … ☆

等式 ★ より、数列 {f(n + 1) － 2f(n)} は、
初項 f(2) － 2f(1) = 20 － 12 = 8 で、公比 4 の等比数列です。

このため、
f(n + 1) － 2f(n)
= 8・4^n－1 … (1)

※ 数列を関数と考えることについては、等差数列は一次関数というブログ記事で解説しています。
　
一方、等式 ☆ より、
数列 {f(n + 1) － 4f(n)} は、
初項 f(2) － 4f(1) = 20 － 24 = －4 で、公比 2 の等比数列です。

このため、
f(n + 1) － 4f(n)
= －4・2^n－1 … (2)

(1) － (2) より、
2f(n) = 8・4^n－1 + 4・2^n－1

この両辺を 2 で割ると、
f(n) = 4・4^n－1 + 2・2^n－1

指数法則より、f(n) = 4ⁿ + 2ⁿ

これで、答えに辿り着きました。
　
ここで使った隣接三項間漸化式の解き方については、リンク先のブログ記事にまとめています。
※ 隣接二項間漸化式を先に解説してからの内容になっています。
　
解と係数の関係と漸化式の融合問題は、大学受験で、しばしば出題されます。

関係式を導くという過程と、関係式から一般項を求めるという過程が必要になります。

その際に、一般的な特性方程式を用いた漸化式の解き方が使えるときは、落ち着いて円滑に一般項を求めることが大切になります。

この記事では２変数の解と係数の関係を扱いましたが、数２で３変数の対称式も出てきます。

それでは、これで今回のブログ記事を終了します。

読んで頂き、ありがとうございました。