自由加群 | 形式的な有限和とは如何なる性質なのか【基底があれば濃度一定】
自由加群 (free module) を学習すると、形式的な有限和が出てきます。これが何なのかということを理解することで、代数学の入門的な内容への理解が深まります。
乗法単位元をもつ可換環上の自由加群に基底があれば、基底の濃度が一定であることも証明しています。
添数づけられた加群の直積の基礎から理解を開始です。
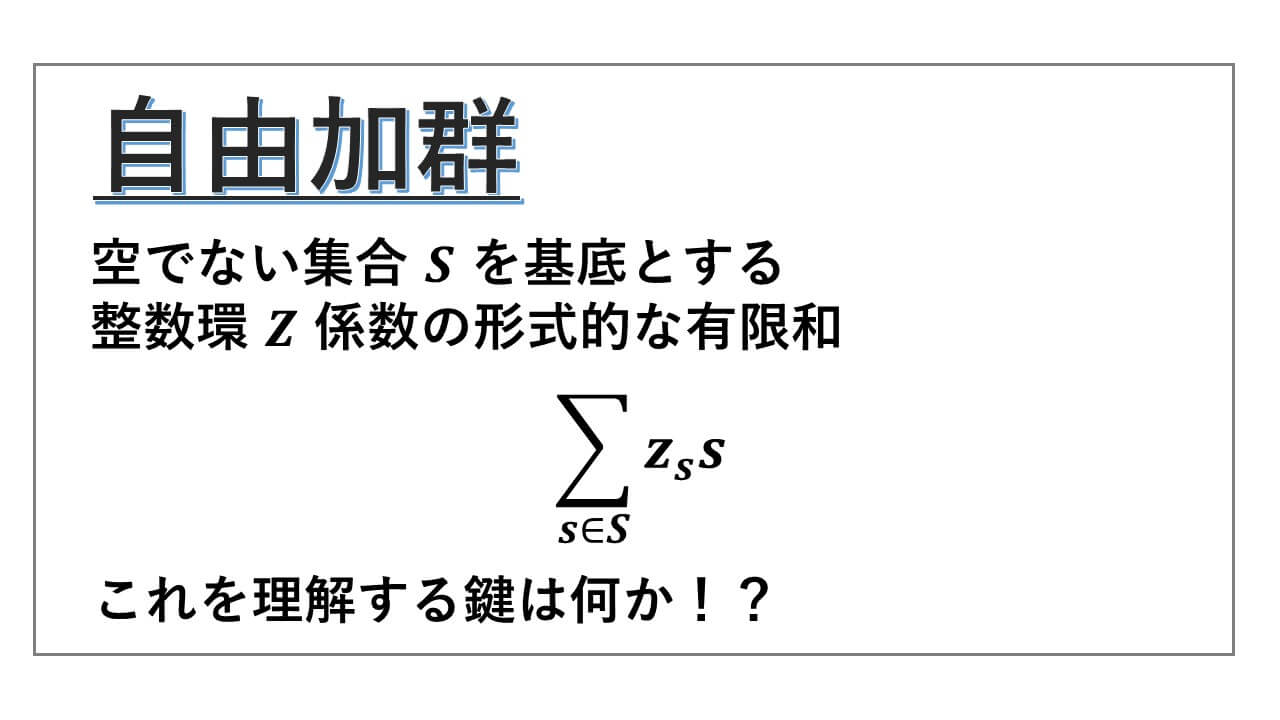
まず、空でない集合 S を基底とする自由加群の定義から説明します。その後で、この定義に使われている形式的な有限和とは何かということを解説します。
なお、このブログ記事では、整数環を Z と表し、R を乗法単位元 1 をもつ可換環としています。
自由加群 :まず定義から
S = {s1, s2, s3} という三つの元からなる集合を基底とする Z-自由加群の定義を述べます。形式的な有限和に触れるために、まずは三個の形式的な和を考えることにします。
S が有限集合のときは、
z1s1+z2s2+z3s3 (z1, z2, z3∈Z)
形式的に zisi という si の横に整数 zi を置いただけの記号の列をすべて集めた集合を作ります。
そして、この集合を M とし、二つの元が等しいということを次で定義します。
【相当関係の定義】
z1s1+z2s2+z3s3 と z’1s1+z’2s2+z’3s3 (z1, z2, z3, z’1, z’2, z’3∈Z) について、
zi=z’i (i = 1, 2, 3) となっているときに限り、
z1s1+z2s2+z3s3 = z’1s1+z’2s2+z’3s3
どの成分についても、横に置かれている整数が同じ整数であるというときに限り、二つの有限和が等しいと定義します。
そして、次のようにして環 Z から M への作用を定義します。
r(z1s1+z2s2+z3s3)
= (rz1)s1+(rz2)s2+(rz3)s3
(r, z1, z2, z3∈Z)
(rzi)si の整数 rzi は、r と zi の通常の整数の積です。そして、rzi は、やはり si の横に置いただけの記号の列です。
さらに、M における加法を次のように定義します。
z1, z2, z3, z’1, z’2, z’3∈Z に対して、
z1s1+z2s2+z3s3 と z’1s1+z’2s2+z’3s3 の加法を、
(z1+z’1)s1+(z2+z’2)s2 +(z3+z’3)s3 とします。
各 si 成分について、横に置かれた整数どおしで、整数の加法を計算したものを si の横に置くというのが加法の定義です。
0s1+0s2+0s3 が M の加法についての零元です。
この加法と Z からの作用について、M は Z 上の自由加群となります。M における相当関係の定義から、S は M の基底となっています。
※ 直積集合への加法やスカラー倍をベクトル空間について考えたときと似ています。
今、三つの元からなる集合を基底とする Z-自由加群を定義したのですが、一般に n 個の有限集合についても、同様の定義です。
S = {s1, … , sn} のとき、
z1s1+ … + znsn という記号列全体を M として、先ほどと同様に相当関係、Z からの作用、M における加法を定義します。
ここで、学習を始めたときに気になるのが、形式的に zisi と記号列を作っていることです。
特に Z から S への作用が定義されているわけでもないのに、横に記号を置いて記号列としています。
これは一体どういうことなのか。これについての答えは、後ほど解説をします。
先に無限集合 S を基底とする Z-自由加群の定義も述べておきます。
無限集合が基底のとき
無限集合 S を基底とする Z-自由加群の定義です。
各 s ∈ S について zs ∈ Z を割り当て、
Σs∈S zss という形式的な和をすべて集めます。ただし、zs は有限個を除いて 0 とします。
有限個を除いて 0 という有限和だけを考えるということは、{s1, … , sk} という S の部分集合を先に指定して、z1s1+ … + zksk という和を考えるということです。
自然数 k を固定すると、無限集合 S から k 個の元からなる部分集合を選ぶ選び方が無限通りあります。
各自然数 k に対して、無限通りの部分集合を選び、それらの各成分について、整数を形式的に横に置きます。
このようにして理論的に作った無限通りの形式的な有限和たちをすべて集めたものを M とします。
【相当関係の定義】
有限和 Σs∈S zss (zs ∈ Z) と
有限和 Σt∈S ztt (zt ∈ Z) が等しいことの定義は、s = t であるとき、zs = zt と必ずなっているということです。
要するに、有限和の係数が 0 となっていない成分があれば、それらの成分について横に置いている整数が、それぞれ等しいということです。
M における加法と、Z から M への作用も定義します。
Σs∈S zss + Σt∈S ztt
= Σs∈S,t=s (zs + zt)s,
rΣs∈S zss = Σs∈S (rzs)s
(r, zs, zt ∈ Z)
やはり成分ごとに加法を定義しています。
どちらも有限和だったので、
zs + zt は有限個を除いて 0 となっています。
この加法と Z からの作用について、M は Z 上の自由加群となります。
では、ここから、形式的な有限和が何なのかということを解説します。
テンソル積の定義にも使われる集合を基底とする自由加群を理解しておくと、代数学の学習が円滑に進むかと思います。
自由加群 :形式的な有限和とは
先に結論を述べると、形式的な和は、外部直積からの同型対応によって得られています。外部直積の元で、有限個の成分を除いて 0 となっているものたちをすべて集めたものが、外部直和です。
この外部直和の各元について、同型対応によって対応しているものが、形式的な有限和です。
何のことはなくて、加群を学習するまでに、既に群や環の入門で学習している内容になります。
ですので、戸惑うことなく、既に学習した内容の類推で加群の外部直積と外部直和を考えると、形式的な有限和が理解できます。
空ではない集合を S とします。
そして、各 s ∈ S について、Zs = Z とします。
このように、各 s で整数環 Z を添数づけておき、これらの直積集合を Πs Zs を考えます。
S が無限集合のときには、Z を無限個で直積したものになっています。
選択公理を集合論の入門で学習したように、直積集合の元は、添数集合 S の各元 s に対して、Zs の元を対応させる写像です。
どのような対応をしているのかを示すために、(zs)s∈S と直積 Πs Zs の元を表すことにします。
(zs)s∈S だと、s ∈ S に対して、zs という Zs の元を対応させていることになります。
Zs は Z という設定だったので、zs は整数です。
直積集合 Πs Zs における相当関係、加法、Z からの作用を次のように定義します。
【相当関係の定義】
(zs)s∈S と (zt)t∈S が等しいとは、
S において s = t であるとき、
zs = zt と必ずなっていることです。
【加法の定義】
(zs)s∈S と (zt)t∈S に対して、
(zs)s∈S + (zt)t∈S = (zs + zt)s∈S,t=s
ここで、zs + zt は、Z における通常の整数の和です。
【Z からの作用の定義】
r ∈ Z と (zs)s∈S に対して、
r((zs)s∈S) = (rzs)s∈S
ここで、rzs は Z における通常の整数の積です。
これで、Πs Zs という直積集合が、Z 上の加群となります。
この外部直積の加群の元について、有限個の成分を除いて 0 となっているものたちをすべて集めた外部直和を M’ とします。
つまり、M’ の元は、
(zs)s∈S という形で、有限個を除いて zs が 0 となっているものです。
M’ は Πs Zs の部分 Z-加群となっています。
では、同型対応で形式的な有限和の正体を理解します。
これで形式的な和が明確に
空でない集合 S に対して、形式的な有限和を考え、Z-自由加群 M を定義しました。
M の元は、Σs∈S zss という形式的な有限和でした。
一方、外部直和を使って、Z-加群 M’ を定義しました。
M’ の元は、(zs)s∈S
ここで、Σs∈S zss に (zs)s∈S を対応させるという写像を考えると、この写像は Z-加群としての同型写像となっています。
そのため、M と M’ が Z-加群として同型になります。同型なので、表面的な表記の記号が違っているだけで、加群としての構造は同じです。
s ∈ S に対して、es ∈ M’ という特別な元を考えます。
s に対して、zs = 1 で、
差集合 Z - {s} の任意の元 t に対して、
zt = 0 という元が es です。
Σs∈Szss = s という M の基底を構成する元 s に対応するのが、es という M’ の元です。
同じ加群構造なら、形式的な有限和の形で自由加群を使うと見やすいこともあります。そこで、このブログサイトでは、テンソル積の定義をするときに、形式的な有限和を使っています。
今、Z-自由加群について考えましたが、一般の可換環 R についても、ここまでの内容の類推が通用します。
空でない集合 S について、
s ∈ S に対して、Rs = R として、Πs Rs という外部直積を R-加群とし、部分加群である外部直和を考えます。
すると、Σs∈S rss に (rs)s∈S を対応させるという写像で、形式的な有限和が、外部直和と R-加群同型となります。
ここまでは、加群の外部直和についての内容でした。ここからは、加群の内部直和についての基底について解説をします。
自由加群 :内部直和について
R-加群が基底をもつとは限りませんが、基底をもつときに、その加群を自由加群といいます。
{aλ}λ∈Λ を R-加群 M の基底とすると、M のどの元も、この基底の一次結合で一意的に表すことができます。
任意の m ∈ M に対して、
m = Σλ∈Λrλaλ (rλ∈R)
ただし、rλ は有限個を除いて 0 という有限和です。
ここで、各 λ ∈ Λ に対して、
{raλ | r ∈ R} = Raλ と表すことにします。
今、Raλ は M の R-部分加群となっていて、
Σλ∈ΛRaλ は、M の内部直和です。
ここで、他に {bμ}μ∈Λ’ という基底があったとき、Λ と Λ’ の濃度が同じということを証明します。
既に示した定理に帰着
{aλ}λ∈Λ と {bμ}μ∈Λ’ が R-自由加群 M の基底だとしたときに、基底の濃度が一定であることを示すときに、ベクトル空間の議論に帰着することを考えます。
ベクトル空間の基底の濃度は一定でした。そこで、ベクトル空間についての議論に帰着させます。
1 をもつ可換環 R には、極大イデアル A が存在します。
そして、R/A は体です。
まず、体 R/A が作用する M に関連する加群を作ることから始めます。
各 λ ∈ Λ に対して、
{raλ | r ∈ A} = Aaλ は、A-加群です。
そして、Σλ∈ΛAaλ は、M の部分集合ですが、A-加群の直和となっています。
さらに、Σλ∈ΛAaλ は、R-加群 M の部分加群になっていることが、次のようにして分かります。
任意の空ではない有限部分集合 T ⊂ M について、Σt∈T rtat (rt ∈ A, at ∈ M) という有限和を考えます。
そして、有限部分集合 T を動かすことで、M で生成される A 上の一次結合全体 N を定義します。

そして、p ∈ R に対して、
p(Σt∈Trtat) = Σt∈Trt(pat)
pat ∈ M なので、A 上の一次結合だから、N の元なので、R の作用で N が閉じていることが分かります。
有限和どおしの和も有限和なので、N が M の R-部分加群ということが分かりました。
つまり、N = Σλ∈ΛAaλ という A-加群の直和が、M の R-部分加群です。
よって、剰余加群 M/N を定義することができます。
x + N と r ∈ R に対して、
r(x + N) = (rx) + N です。
体 R/A の元について、
r + A = p + A とすると、
ある α ∈ A が存在し、r = p + α
任意の x ∈ N に対して、αx ∈ Nのため、
r(x + N) = (rx) + N
= (p + α)x + N
= (px + N) + (αx + N)
= (px + N) + (0 + N)
= (px) + N = p(x + N)
よって、r + A ∈ R/A から
x + N ∈ M/N への作用を
(r + A)(x + N) = (rx) + N と矛盾なく定義できます。
したがって、体 R/A 上のベクトル空間 M/N が定義できました。
このベクトル空間の基底が何かを考えます。
記号をシンプルにするために、
r + A ∈ R/A を [r]A、
x + N ∈ M/N を [x]N と表すことにします。
M/Nの基底は何か
{aλ}λ∈Λ が M の基底だったので、
{aλ+N}λ∈Λ によって、M/N が生成されています。
実は、これが、一次独立で、M/N の基底となっています。
{λ1, … , λk} を任意の Λ の有限部分集合とします。
もし、[r1]A[aλ1]N+…+[rk]A[aλk]N = [0]N だとすると、
[r1aλ1+…+rkaλk]N = [0]N
よって、
N ∋ r1aλ1+…+rkaλk = Σλ∈ΛAaλ (内部直和)
aλ1, … , aλk は、R-加群 M の基底の元なので、r1, … , rk は A の元ということになります。
ゆえに、
[r1]A=…=[rk]A=[0]A = 0 + A ∈ R/A
これで、{aλ + N}λ∈Λ が一次独立でもあり、
M/N の基底であることが示せました。
さらに、もう一つの M の基底について、同様に、Σμ∈Λ’ Abμ は A-加群の直和で、M で生成される A 上の一次結合全体 N に一致しています。
よって、上で述べた議論を踏襲することによって、{bμ + N}μ∈Λ’ も M/N の基底であることが分かります。
体 R/A 上のベクトル空間 M/N の基底の濃度が一定であるため、
Λ と Λ’ の濃度は同じということになります。【証明完了】
これで、今回のブログ記事を終了します。
読んで頂き、ありがとうございました。