選択公理 | 同値な命題たちもともに内容を把握【入門的な記号の使い方と定義】
選択公理 (axiom of choice) は、一般の直積の定義の把握を正確に押さえると、内容が分かってきます。
この一般の直積の定義を理解するためには、添数集合の記号の使い方を把握しておく必要があります。
写像の一対一対応をきっちりと把握することが理解の近道になるかと思います。
添数集合の元（要素）とそれに対応するものを表すときの記号の使い方ですが、数列の対応関係は参考になります。
自然数 n に対して、その写像 a による像 a(n) のことを an と表す記号の使い方は、添数集合の元に対して対応する像の値を表すことを習得するのに役立つかと思います。
選択公理に関連する入門的な集合論の内容を学習するときに、添数集合 Λ から集合 S の写像（関数） a の記号の使い方を押さえておくと、理解がしやすいです。
選択公理 :記号の使い方から
a : Λ → S という写像で、λ ∈ Λ に対して、像が a(λ) ∈ S です。この像 a(λ) のことを aλ と書くときも多いです。
また、写像なので、定義域 Λ について、値域は集合の記号で表すと、{a(λ) | λ ∈ Λ}となります。
S への写像なので、これは S の部分集合となっています。a(λ) = aλ は S の元です。この値域という集合を、(aλ)λ∈Λ と表すときもあります。
この添数集合の具体例として、高校の数学で出てきた数列の記号の使い方が挙げられます。
添数集合が自然数全体 N で、N から実数全体 R への写像が a だとします。
n ∈ N に対して、a(n) = 5n などと、写像 a の対応規則があります。
4 に対して、a(4) = 5 × 4 = 20 です。
a4 = 20 という表し方を高校の数学ではしていました。この写像 a の値域のことを (an)n∈N と大学の数学では表すこともあります。
添数集合 N で N の元 n のかわりに、Λ と λ が大学の数学では、よく使われます。同じ要領で使いながら、記号の使い方に慣れていくと良いかと思います。
集合族
先ほど、添数集合 Λ の元 λ に対して、集合 S の元を対応させていました。この λ に対して、1 つの集合を対応させるときもあります。
各 λ ∈ Λ に対して、対応する集合を Aλ とするときに、対応してくる集合をすべて集めた集まりのことを、{Aλ | λ ∈ Λ}と表します。
※ Λ からの対応を表す写像のことを (Aλ)λ∈Λ と表します。添え字づけられた集合たち全ての和集合を終集合とします。∪λAλ が終集合です。
各 λ∈Λ に対して、Aλ を対応させている集合族という写像 (Aλ)λ∈Λ が与えれれると、上のように対応する集合たちをすべて集めたものが認識できます。
※ 記号の使い方は、大学の講義などでも、集合の集まりの方も集合族といわれることがあります。どういう使われ方をされているのかは、毎回チェックをしておくと良いかと思います。
単純な例で、集合族によって集められた集合たちを確認してみます。
Λ = {1, 2, 3} とします。
1 に対応する集合が A1 = {5}、2 に対応する集合が A2 = {6, 7}、3 に対応する集合 A3 が空集合 Φ とします。
集合族 (Aλ)λ∈Λ によって、対応する集合たちの集まりは、
{A1, A2, A3} = {{5}, {6, 7}, Φ}
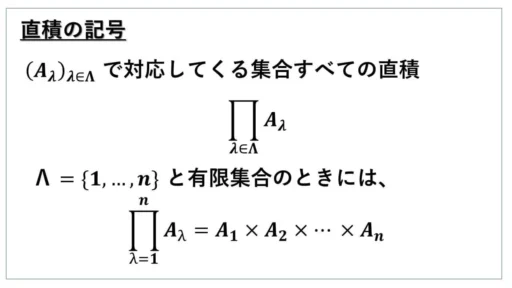
ここまでの記号の使い方を押さえた上で、一般の直積の元が何かということを把握します。
この把握に誤りがあると、選択公理が何を表しているのか、分からなくなってしまうので、「一般の直積」の定義には注意です。
選択公理 :一般の直積の定義
Λ を添数集合とする集合族 (Aλ)λ∈Λ についての集合たちの集まりがあったとします。
先ほどの例では、Λ が有限個のときを述べましたが、Λ が無限集合というときもあります。
ここで、(Aλ)λ∈Λ による集合たちの集まりに含まれている集合について、それらすべての直積を表す記号を説明します。
また、直積の元とは何かということについても説明します。
添数集合 Λ が有限集合のときには見慣れた直積の記号をしています。しかし、一般の直積の元の定義は、認識をしっかりとしておく必要があります。
＜直積の元＞
直積の元は、次の条件(*)を満たす添数集合 Λ を定義域とする写像 aです。
条件 (*) : 各 λ ∈ Λ に対し a(λ) ∈ Aλ
※ a(λ) のことを aλ と表すときもあります。
この条件 (*) を満たす写像たちをすべて集めた集合が直積です。
この一般の直積の定義を押さえていないと、選択公理だけではなく、現代数学で添数集合が無限集合のときの理解がおかしくなってしまうので、注意です。
この直積についての定義を押さえると、多項式環の不定元といった内容を理解することへとつながります。
Λ が有限集合のときには、今まで使ってきた直積の認識からすると違和感があるかと思います。それは、有限個の直積のときには、書き換えがあります。
有限個の直積については、次の書き換えた方を通常は使います。
有限個の直積の書き換え
Λ = {1, 2} という二個の直積のときの書き換えです。
条件 (*) を満たす写像 a が与えられたときに、
a1 ∈ A1, a2 ∈ A2 となっているため、
(a1, a2) という組が形成できます。
逆に、(s, t) という組で、
s ∈ A1, t ∈ A2 となっているものが与えられると、Λ を定義域とする条件 (*) を満たす写像 a を、a(1) = a1 = s, a(2) = a2 = t と定義できます。
以上より、
「条件 (*) を満たす Λ を定義域とする写像が与えられること」の必要十分条件が、「(s, t) という組で、s ∈ A1, t ∈ A2 となっているものが与えられること」となります。
このため、写像を使った一般の直積の元の定義を、見慣れた組を使った定義に書き換えることができます。
今、二個の直積についての書き換えを述べましたが、一般に A1 から An までの n 個の直積について組を用いた書き換えが可能です。
(a1, a2, … , an) という n 個のそれぞれの集合の元から成る組で表すことができます。
一般的に数学の議論で、添数集合 Λ が有限集合のとき、有限個の直積の元は組を使って表されることが多いです。
しかし、添数集合 Λ は無限個のとき、自然数全体のように大小関係の順番が定義されていないというときさえあります。
添数集合 Λ が無限集合のときには、無限個の元たちの組というものを無理に表そうとはしないで、条件 (*) を満たす写像の方で表されます。
＜注意点＞
条件 (*) で、各 λ ∈ Λ に対して、a(λ) ∈ Aλ とありました。a(λ) ∈ Aλ ということについて、満たさない例も書いておきます。
有限個のときのシンプルな例です。
Λ = {1, 2} で、A1 と A2 はどちらも実数全体 R としておきます。
Λ を定義域とする次の写像が直積 R × R の元かどうかを判断してみます。
f(1) = 5, f(2) を 3 行 3 列の実数を成分とする単位行列とします。
この f は確かに Λ を定義域としています。そして、f(1) = 5 ∈ R = A1 となっています。
しかし、f(2) は実数を成分とする 3 行 3 列の行列なので実数ではないため、R には含まれません。
そのため、f(2) は A2 = R に含まれていません。
したがって、条件 (*) を満たしていないので、この f は直積 R × R の元ではないということになります。
添数集合 Λ のそれぞれの元 に対して、なんでもかんでも値を対応させれば良いというわけではないということです。
値を対応させたとしても、a(λ) が Aλ に含まれないときもあるということを知っておくと、選択公理についての実感がもてるかと思います。
選択公理 :選択公理を眺めてみよう
これが選択公理です。公理というくらいで、現代数学では、この内容を証明なしで認めた上で数学の理論体系が構築されています。
どの添え字 λ についても、Aλ が空集合でないとき、それらの集合たちすべてで直積をつくると、その直積は空集合ではないという内容です。
直積の元の定義は、 条件 (*) : 各 λ ∈ Λ に対して、a(λ) ∈ Aλ を満たす写像 a のことです。
この選択公理を認めているので、
抽象的な { Aλ | λ ∈ Λ }、つまり (Aλ)λ∈Λ に含まれているそれぞれの集合について、条件 (*) を満たす写像 a が少なくとも 1 つは存在するということが保証されています。
※ 各 λ に対して、Aλ のことを直積因子といいます。
Λ が無限集合のときの無限個の直積のときは、この条件 (*) を満たす写像が直積の元です。
写像なので、定義域のどの値 λ に対しても対応する値 a(λ) が定まっていて、しかも Aλ に含まれているということです。
先ほど、f(2) が 3 行 3 列の単位行列という写像を定義したら、条件 (*) に当てはまりませんでした。
条件 (*) を満たす写像という定義で考えると、選択公理を本当に認めて良いのかと思えてしまいます。
しかし、歴史的には、有限個の直積について、直積の元が有限個の元を一斉に選び出した組のようなイメージもあり、ごく当たり前の内容として選択公理のことが考えられたかもしれません。
論争になったそうですが、現在においては、選択公理は認められています。
ただ、歴史的な背景とは別に、選択公理を使わずに直積が空集合ではないことを示せるときもあるということを知っておくと良いかと思います。
無条件で認められていますが、少しでも具体的に扱える論拠の方が良いという認識です。
無限個の集合の直積だけれども、選択公理を使わずに空集合と言える例を紹介します。
公理なしで空集合でないことが言える例
【例】
自然数全体 N を添数集合とします。各 n ∈ N に対して、An を実数全体 R とします。
このとき、(An)n∈N について、各自然数に対応する集合すべての直積は空集合ではありません。
選択公理を使わない典型例は、直積の元の定義である条件 (*) を満たす写像を具体的に自分で定義できる場面です。
この【例】の場合、添数集合 N の各 n に対して、a(n) = 0 ∈ An = R と定義します。
どの自然数 n についても、実数の 0 を対応させるという写像は、添数集合 N を定義域とする写像で条件 (*) を満たしています。
条件 (*) を満たす写像が 1 つでもあることが示せれば、無限個の直積が空集合ではないということになります。
ここまでで、無限個の直積に焦点を当てて述べました。有限個の直積集合については、リンク先の記事で詳しく解説をしています。
ここで、順序集合における極大元の定義を述べておきます。
【極大元の定義】
S を ≦ を順序とする順序集合とする。
a ∈ S について、a < x となる S の元 x が存在しないとき、a を S の順序 ≦ についての極大元といいます。
否定についての論理を考えると、
a ∈ S が極大元でないときは、ある y ∈ S が存在して、a < y となるということです。
ここからは、選択公理を使って、命題を 1 つ証明してみます。
抽象的な状況で、添数集合から、それぞれの直積因子への写像の存在が示されることが効果を発揮する命題です。
※ この命題を証明するときに、添数集合が集合の集まりとなっているので、ご注意ください。
選択公理を用いて命題を証明する
【命題 1】
≦ を順序とする順序集合 S が極大元を持つとする。
このとき、S から S への写像 f が存在して、任意の x ∈ S に対して、f(x) > x となる。
＜証明＞
S の空でない部分集合をすべて集めた集合の集まりを Λ とします。
Λ の各元 T に対して、T 自身を対応させる集合族を ( T )T∈Λ と表すことにします。
どの T ∈ Λ も空集合ではないので、
選択公理により、
ある写像 φ が存在して、φ(T) ∈ T
この φ は ( T )T∈Λ による一般の直積の元で、それぞれの直積因子 T に対して、T に含まれる 1 つの元を対応させています。
それぞれの T から一斉に 1 つずつ元を取るということを写像 φ を使って表しています。
各 x ∈ S に対して、
Sx = {y ∈ S | x < y} という S の部分集合を考えます。
S には極大元が存在しないので、x が極大元でないことから、x よりも大きい S の元が存在するため、Sx は空集合ではありません。
よって、Λ の定め方から、各 x ∈ S に対して、Sx ∈ Λ となっています。
すると、φ によって、
Sx に対応する値 φ(Sx) ∈ T が定まります。
ゆえに、x ∈ S に対して、φ(Sx) ∈ T ⊂ S を対応させる写像を f と定義すると、
f : S → S
x → φ(Sx) となっています。
x の f による像は、f(x) = φ(Sx) です。
φ(Sx) ∈ Sx でした。
Sx の定め方から、φ(Sx) > x となっています。
すなわち、f(x) > x ということです。
これで、S から S への写像 f で、各 x ∈ S について、f(x) > x を満たすものが定義できました。【証明完了】
この【命題 1】は、強い条件で述べられツォルンの補題を証明するときに使えます。この強い条件というのは、次の意味でです。
【強い帰納的の定義】
順序集合 S について、「S の任意の空ではない全順序部分集合が、包含関係を順序としたときに、必ず S の中に上限をもつ」とき、S を強い意味で帰納的といいます。
代数学の入門などで用いられる Zorn の補題でいう帰納的と、定義が少し違った言い方をしています。
選択公理から、まず、この強い意味の帰納的を用いたツォルンの補題が、導かれます。
先ほどの【命題 1】と、次の【命題 2】を用いると、強い意味の帰納的を用いたツォルンの補題を得ます。
【命題 2】
≦ を順序とする 強い意味で帰納的な順序集合を S とします。
そして、S から S への写像 f が、各 x ∈ S に対して f(x) ≧ x を満たすとします。
このとき、ある a ∈ S が存在して、f(a) = a となります。
この【命題 2】は、整列集合についての比較定理などの準備を土台として導かれます。
かなり長くなるので、このブログ記事では証明を割愛して使います。
では、強い意味の帰納的を用いたツォルンの補題を証明します。
【強い意味のツォルンの補題】
強い意味で帰納的な ≦ を順序とする順序集合 S は、少なくとも 1 つ極大元をもつ。
＜証明＞
背理法で示します。
もし、S に 1 つも極大元が存在しなかったと仮定すると、【命題 1】から、S から S への写像 f が存在して、任意の x ∈ S に対して f(x) > x となります。
強い意味の順序集合 S と f について、【命題 2】を適用すると、ある a ∈ S が存在して、
f(a) = a となります。
しかし、任意の x ∈ S に対して f(x) > x となるため、f(a) = a と矛盾します。
よって、背理法から、S には少なくとも 1 つは極大元が存在することになります。【証明完了】
選択公理と同値な命題たち
先ほど選択公理から導かれた強い意味のツォルンの補題ですが、テューキーの有限的な性質を介した定理を用いることで、次の一般的に用いられる Zorn の補題が導かれます。
【Zornの補題】
≦ を順序とする順序集合 S において、任意の空でない全順序部分集合が上に有界ならば、S は少なくとも 1 つ極大元をもつ。
先ほどの強い意味のツォルンの補題では、上限でした。
上限は、すべての上界の中で最小の値です。それに対して、Zornの補題では、上に有界なだけで良いというわけです。
すなわち、1 つでも上界が存在すれば良いわけなので、上限が存在するよりも弱い条件になります。
ところが、強い意味のツォルンの補題も、この Zornの補題も同値ということが証明されています。
テューキーの有限的な性質を用いて、複数の同値な命題に強い意味のツォルンの補題に書き換えられます。
ちなみに、ツォルンの補題から、整列定理が導かれます。「集合 A に適当な順序を定義して、A をその順序について整列集合とすることができる」というのが整列定理です。
そして、整列定理から、次のようにして、選択公理が導かれます。
ぐるっとまわって、すべて同値な命題ということになります。
【整列定理から選択公理】
Λ を添数集合とする空でない集合たち Aλ (λ ∈ Λ) が与えられたとします。
このとき、A = ∪λAλ とこれらの集合たち全てで和集合をとります。
A に整列定理を適用して、ある順序 ≦ について、A が整列集合となります。
すると、各 λ ∈ Λ に対して、Aλ ⊂ A なので、整列集合の定義から、Aλ には最小元 min Aλ が存在します。
よって、λ ∈ Λ に対して、
f(λ) = min Aλ とすると、f は f(λ) ∈ Aλ を満たす Λ から ∪λAλ への写像となっています。
そのため、f ∈ ΠλAλ なので、直積 ΠλAλ は空でないということになり、選択公理が導かれました。【証明完了】
すべての証明を理解するのは大変ですが、数学についての基礎的な事実として、知っておくと良いかと思います。
先ほど整列集合についての内容を述べましたが、整列集合に関連して超限帰納法という証明論法が得られます。
関連する内容として、リンク先のブログ記事で解説をしています。
自然数全体が整列集合となっているということから、帰納法について解説をしています。
ツォルンの補題を使う例として、無限次元ベクトル空間の基底の存在についての記事も投稿しています。
これで、今回のブログ記事を終了します。
読んで頂き、ありがとうございました。