確率変数の独立 | 積についてE(XY)、和についてV(X+Y)の公式が独立だからこそ成立

2023年4月14日

" 確率変数の独立 “について、積に関しては、
E(XY) = E(X)E(Y) が成立します。

和に関しては、
V(X+Y) = V(X) + V(Y) となります。

さらに独立と関係なく成立する公式と合わせて、
V(aX+bY) = a²V(X) + b²V(Y) も導きます。

記事の終盤で、事象の独立について触れています。

それでは、確率変数 X と Y が独立なときに、積 XY と和 X + Y に成立する公式について解説します。

確率変数の独立 :積についてE(XY)

確率変数 X と Y について、X の取る値が a で、Y の取る値が b であるときに使う記号から説明します。

「X の値が a であり、かつ、Y の値が b となる確率」を表す記号を、
P(X =a, Y = b) と表します。

確率変数 X と Y が互いに独立なとき、
P(X =a, Y = b)= P(X = a)P(X = b) です。

P(X = a) と P(X = b) を掛け合わせるだけで良いので、独立なときは計算しやすくなります。

高校一年のときに、確率の単元で、二つの試行が独立ということを学習しました。

片方の結果が、もう片方へ影響を及ぼさないことが試行の独立で、独立試行の確率について、確率どおしの積を計算しました。

同じ要領で、確率変数が独立なときは、
P(X = a) と P(X = b) を掛け合わせます。

確率変数 X と Y が独立なときに成立する公式について、確率変数の積 XY についての期待値に関する公式があります。

XYの値を論理的に観察

【X と Y が独立なとき】
確率変数 X が取る値が、x₁, x₂ だとし、それぞれが起こる確率が、
P(X = x₁) = p₁, P(X = x₂) = p₂ だとします。

確立変数 Y が取る値を y₁, y₂ とします。
そして、それぞれが起こる確率を、
P(Y = y₁) = q₁, P(Y = y₂) = q₂ とします。

X と Y が互いに独立なとき、期待値 E(XY) の値が、どうなっているのかを解説します。

X と Y について、それぞれの値が起こる確率が与えられている状況です。

そこで、X, Y の同時分布についての確率を考えます。

P(Y = y₁) = q₁ となるとき、次の場合が考えられます。

X = x₁ の場合と X = x₂ の場合が考えられます。

X と Y が互いに独立なので、
X = x₁ かつ Y = y₁ である確率は、
P(X = x₁)P(Y = y₁) = P(XY = x₁y₁)

P(X = x₁) = p₁, P(Y = y₁) = q₁ だったので、
XY の値が x₁y₁ である確率は、
P(XY = x₁y₁) = p₁q₁

Y = y₁ のとき、X = x₂ となる場合も考えられるので、XY の値が x₂y₁ となる確率も同様に計算できます。

P(XY = x₂y₁) =
P(X = x₂)P(Y = y₁) = p₂q₁

XY の期待値を求めるために、残りの可能性についても、起こる可能性を計算します。

Y = y₂ のとき、
X = x₁ または X = x₂ です。

P(XY = x₁y₂) =
P(X = x₁)P(Y = y₂) = p₁q₂

Y = y₁ かつ X = x₂ のときも確率を計算します。

P(XY = x₂y₂) =
P(X = x₂)P(Y = y₂) = p₂q₂

これで、確率変数 XY が取る値と、それぞれの起こる確率を全て求めました。

ここまでの内容から、期待値を計算できます。

E(XY)を求める

XY の値が x₁y₁ となる確率は、
P(XY = x₁y₁) = p₁q₁

XY の値が x₂y₁ となる確率は、
P(XY = x₂y₁) = p₂q₁

XY の値が x₁y₂ となる確率は、
P(XY = x₁y₂) = p₁q₂

XY の値が x₂y₂ となる確率は、
P(XY = x₂y₂) = p₂q₂

確率変数 XY の取る値と、その値となるときの確率を掛け合わせたものを全て足し合わせたものが、期待値の定義です。

よって、
E(XY) =
(x₁y₁)(p₁q₁)+(x₂y₁)(p₂q₁)
+(x₁y₂)(p₁q₂)+(x₂y₂)(p₂q₂)
= (x₁p₁+x₂p₂)(y₁q₁+y₂q₂)

したがって、
E(XY) = (x₁p₁+x₂p₂)(y₁q₁+y₂q₂)
= E(X)E(Y)

【まとめ】

確率変数 X と Y が互いに独立なとき、
E(XY) = E(X)E(Y)

ちなみに、X と Y が独立であっても、独立でなくても、
E(X + Y) = E(X) + E(Y) となっています。

確率変数が X, Y, Z と三つあるときにも、X, Y, Z が互いに独立であることの定義があります。

X, Y, Z が互いに独立であるときに、
期待値について、
E(XYZ) = E(X)E(Y)E(Z) が成立します。

それでは、X と Y が互いに独立であるとき、分散について役立つ公式を証明します。

確率変数の独立 :和についてV(X+Y)

【公式】
確率変数 X と Y が互いに独立なとき、
V(X + Y) = V(X) + V(Y)

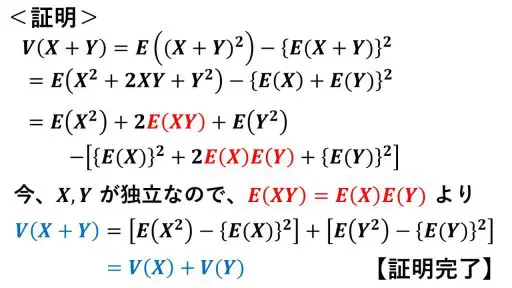
また、X と Y が独立であっても、独立でなくても、定数 t について、
V(tX) = t²V(X) が成立します。

今、証明した公式と、V(tX) = t²V(X) を合わせると、次の公式が得られます。

V(aX+bY)の公式

【公式】
確率変数 X と Y が互いに独立であるとする。
a, b を定数とする。

このとき、
V(aX + bY) = a²V(X) + b²V(X)

＜証明＞

X と Y が独立なので、分散の和の公式から、
V(aX + bY) = V(aX) + V(bY)

さらに、V(aX) = a²V(X),
V(bY) = b²V(X) だから、

V(aX + bY) = a²V(X) + b²V(Y)【証明完了】

ちなみに、三つの確率変数 X, Y, Z が互いに独立なとき、定数 a, b, c について、
V(aX + bY + cZ) =
a²V(X) + b²V(Y) + c²V(Z) が成立します。

練習問題

【練習問題１】

表の出る確率が p (0 < p < 1) である百円玉を 2 回投げます。

1 回目に表が出たら X = 1,

1 回目に裏が出たら X = 0,

2 回目に表が出たら Y = 1,

2 回目に裏が出たら Y = 0

とすることにより、確率変数 X と Y を定義します。

a, b, c を p に無関係な定数とするとき、
Z = aX + bY + cXY という確率変数の期待値 E(Z) を求めてください。

＜解説と答え＞

1 × p + 0 × (1 － p) より、
E(X) = p, E(Y) = p

ここで、X と Y は独立だから、
E(Z) = E(aX + bY + cXY) =
aE(X) + bE(Y) + cE(XY)

さらに、X, Y が独立なので、
E(XY) = E(X)E(Y) より、
E(Z)= aE(X) + bE(Y) + cE(X)E(Y)
= ap + bp + cp²
= cp² + (a + b)p【答え】

もう一つ独立についての練習問題です。

【練習問題２】

X と Y が互いに独立な確率変数とします。
V(X) = 3, V(Y) = 4 のとき、
V(2X + 5Y) の値を求めてください。

＜解説と答え＞

X と Y が互いに独立なので、分散の和の公式から、
V(2X + 5Y) = 2²V(X) + 5²V(Y)
= 4×3 + 25×4 = 12 + 100 = 112【答え】

ここからは、よく似た名前ですが、内容が異なる数Bの確率の用語について説明をします。

事象の独立 :定義と記号

ここで、
P(A ∩ B) は、事象 A ∩ B が起こる確率を表しています。

P(A), P(B) についても、それぞれ事象 A, B が起こる確率を表す記号です。

P(A) ≠ 0, P(B) ≠ 0 のときは、
確率の乗法定義が成立するということです。

P_A(B) = P(A)P(B),
P_B(A) = P(B)P(A) = P(A)P(B) という条件付き確率で学習した内容です。

数学Bで学習するときには、条件付き確率の内容を理解していることを前提として議論が進みます。

ここで、ややこしいのが、確率変数を用いた内容が絡むことです。

日常語とのギャップ

独立ということについて、上で述べた確率変数の独立がありました。

高校数学の内容では、この二つは同値として扱われます。

同値ということは、書き換えが可能ということです。

そこで、二つの確率変数が独立ということの定義を見てみます。

【定義２】

ある試行において、確率変数 X と Y が取る値が、X が a で、かつ Y が b であるとする。

このとき、
P(X = a, Y = b) で X が a で、かつ Y が b である確率を表す。

そして、
a と b の値に関わらず、
P(x = a, Y = b)
= P(x = a)P(Y = b) となっているとき、二つの確率変数 X と Y が独立であると定義する。

「事象 A と事象 B が独立」ということと、「確率変数 X と Y が独立」ということが同値であると述べられることもあります。

「事象 A, B と対応する確率変数 X と Y の関係から」と、さらっとスルーされることが多いです。

この言い方ですが、分かったようで分かりにくい内容です。

そこで、
X = a となるときの事象を A, Y = b となるときの事象を B と置くことにした上で、a と b の値に関わらず、
P(A ∩ B) = P(A)P(B) が成立すると考えます。

すると、これは、
P(X = a, Y = b)
= P(X = a)P(Y = b) と同じことを表します。

a と b の値に関わらず成立するということは、a と b として起こり得る全ての値について、それぞれの等式が成立するということです。

なお、一般に、事象の独立が成立していても、試行の独立が成立するとは限りませんので注意です。

「事象が独立」ならば、「試行が独立」は、一般的に成立するとは限らないという事実だけを述べるに留めておきます。

【関連記事】

■ 反復試行の確率

■ 二項分布

これで、今回の記事を終了します。

読んで頂き、ありがとうございました。