反復試行の確率 | サイコロを投げることを繰り返す試行についての全事象

反復試行の確率 (同じ試行を n 回繰り返したときの確率)について、公式が示す意味を考察します。
さらに理解を深めるために、集合について、発展内容とされている用語(直積)を使います。
ただ、用語だけが使われていないだけで、公立の中学の確率単元でも実質的な内容は使われています。
踏み込んだ理解をするための全事象の把握です。
表紙の画像に書いている確率の式の意味を解説した後、このサイコロを 4 回投げることを繰り返す反復試行について、全事象を考察します。
全事象が明確に把握できると、反復試行の確率の公式の内容がさらに深く理解できます。
また、数学Bの二項分布(ベルヌーイ分布)へとつながります。
そして、大学の数学で頻繁に使う直積についての良い学習例となるかと思います。
それでは、シンプルな具体例を使って、反復試行の公式が示す意味を解説します。
反復試行の確率 :公式が表す意味
【具体例】
サイコロを 4 回続けて投げるという試行を考えます。
このとき、1 の目が 4 回中 3 回出る確率は、
4C3(1/6)3(1 - 1/6)4-3 となります。
いきなり 4 回連続の全事象(全体集合)を考えるのは大変なので、1 回サイコロを投げたときについて、どのような確率の理論が構成されているのかを考えます。
1 回目にサイコロを投げたときに、出る目の可能性は、1 から 6 までの 6 通りの目の出方があります。この目の出方を全て集めた集合を S1 と表すと、
{1,2,3,4,5,6} = S1 です。
そして、「1 の目が出る」という条件を、条件 p とします。
条件 p を満たすのは 1 のみなので、S1 の要素で条件 p を満たすものを全て集めた部分集合を A とすると、A は 1 点集合となります。
つまり、
A = {1} ⊂ S1 です。
1 回サイコロを投げたときの起こり得る場合の総数は、S1 に含まれている要素の個数なので、n(S1) = 6 通り
※ n(S1) は S1 に含まれている要素の個数を表す記号です。
条件 p を満たす場合の総数は、A に含まれている要素の個数なので、n(A) = 1 通り
よって、1 回目にサイコロを投げたときに、条件 p を満たす確率は、
n(A) ÷ n(S1) = 1 ÷ 6 = 1/6
ここで、条件 p を満たさない確率も考えます。確率の単元の用語では、A の余事象が、条件 p を満たさない S1 の要素全体です。
A の余事象と難しそうな用語が使われていますが、既に学習している A の S1 における補集合 Ac のことです。
Ac は条件 p を満たさない S1 の要素を全て集めたものなので、
{2,3,4,5,6} = Ac
よって、条件 p を満たさない確率は、
n(Ac) ÷ n(S1) = 5 ÷ 6 = 5/6
1回の試行における二択
1 回のサイコロを投げるという試行において、「1 の目が出る」という条件 p を満たすか、満たさないかのいずれか一方のみが起こります。
サイコロの目が条件 p を満たせば、A の要素となります。
条件 p を満たさなければ、補集合 Ac の元になります。
S1 = A ∪ Ac かつ A ∩ Ac は空集合 Φ です。
このように、S1 は、A と Ac に二分割されています。
※ A と Ac は互いに排反です。
※ 同様に確からしいという記事で、集合単元の用語について説明をしています。
そのため、S1 の要素は、A の要素か Ac の要素かのいずれか一方のみということになります。
要素の個数について、
n(Ac) = n(S1) - n(A) = 6 - 1
よって、1/n(S1) を両辺に掛けると、
n(Ac)/n(S1) = 1 - 1/6
1/6 は A が起こる確率でしたから、A の余事象の確率は 1 から A が起こる確率を引いたものということになります。
これで、1 回サイコロを投げたときに起こる場合についての確率が求まりました。
条件 p を満たす確率
(1 が出る確率)1/6
条件 p を満たさない確率
(1 が出ない確率)1 - 1/6
1 回の試行において、1 の目が出るか、1 の目が出ないかのいずれか一方のみとなり、それぞれの確率が求まりました。
ここまでの情報から、4 回連続でサイコロを投げたときの確率を考えます。
4回中3回起きるとは
今、1 回目の試行について考えました。2 回目、3 回目、4 回目とも、1 回目と同じ状況が繰り返されています。
どの回であっても、1 が出る確率が 1/6 で、出ない確率が 1 - 1/6 です。
4 回のうち、1 の目が 3 回出るということは、三つの回で 1 が出て、一つの回で 1 が出なかったということになります。
1 の目が出ることを 〇、1 の目が出ないことを × と表すと、1 の目が 4 回中 3 回出るということの可能性は、次の 4 つのパターンです。
〇〇〇×
〇〇×〇
〇×〇〇
×〇〇〇
4 回中 3 つが 〇 ということなので、この 4 通りは、組合せの記号を用いると、4C3 通りとなっています。
反復試行において、1 回 1 回の試行は独立で、一つの試行が他の試行に影響を及ぼさないという前提になります。
そのため、独立な試行の確率なので、各試行における確率の掛け算となります。
1 の目が 3 回でるので、1/6 が 3 回起き、
5/6 が (4 - 3) 回起きています。
そのため、4C3 通りのうちの、
どの一つの状況についても、
(1/6)3・(1 - 1/6)4-3
これが、全部で 4C3 通りあるので、
求める確率は、
4C3(1/6)3・(1 - 1/6)4-3
これで、反復試行の確率を求めたのですが、最後の方の解説が分かりにくいものになっているかと思います。
これは、4 回連続で投げたときの全事象を求めていないからです。
独立な試行についての確率の一般法則だけで推論を進めたために、イメージがしにくいものになっています。
そこで、直積集合を用いて、4 回の試行を繰り返したときの全事象を明らかにします。
直積集合という用語は、高校数学の発展内容となっていますが、実質的に中学や算数のときの場合の数・確率の学習で使っています。
単純な内容なので、直積の内容に踏み込んでみると、より理解が深くなるかと思います。
反復試行の確率 :全事象を求める
1 回目のサイコロの出る目を集めた集合が S1 でした。
2 回目のサイコロの出る目を集めた集合を S2 とすると、
{1,2,3,4,5,6} = S2
3 回目, 4 回目のサイコロの出る目を集めた集合をそれぞれ S3, S4 とすると、どちらも同じ集合です。
やはり、{1,2,3,4,5,6} です。
これで、S1 から S4 までの集合を具体的に書き出しました。
これら 4 個の集合の直積集合の要素は、次のように 4 個の成分でできている組となります。
(a1, a2, a3, a4) です。
この a3 だと、S3 のどれかの要素ということです。
大学の数学の表し方をすると、
ai ∈ Si (i = 1, 2, 3, 4) ということです。
直積に慣れるために、具体的に直積の要素を述べます。
4 回サイコロを投げたとき、次のような目の出方になっていたとします。
1 回目が 5、2 回目が 3、3 回目が 4、4 回目が 1 というときを直積集合の要素で表すと、
(5, 3, 4, 1) となります。
文で述べると長いですが、直積の要素の記号を使うと、端的に内容を表現できます。
(2, 6, 2, 3) だと、1 回目と 3 回目にサイコロの目が 2 だったということになります。第 1 成分と第 2 成分の値が 2 となっていることが表す内容となります。
このような 4 つの成分からできている組全体を集めた集合が直積集合で、次の記号で表します。
S1×S2×S3×S4 という表し方になります。
和集合 ∪、共通部分 ∩ と違った直積の記号が「×」です。第 i 成分が Si の要素となっている組全体が、S1 から S4 までの集合の直積集合です。
S1×S2×S3×S4 が、4 回サイコロを投げるという反復試行によって発生する全事象(全体集合)です。起こり得る場合の総数が、この直積集合に含まれている要素の個数です。
では、その総数を求めてみます。
全事象の要素の個数
Si (i = 1, 2, 3, 4) は、どれも 6 個の要素なので、
n(S1×S2×S3×S4) = 64
6×6×6×6 なので、64 個の組が要素となっています。確率を求めるときに、最後に割る数で、分母にくる数となります。
※ 約分できるときは約分します。
「1 の目が 4 回中 3 回出る」という条件を満たす場合が何通りあるのかも、計算します。
〇〇〇× が、4 回目が 1 が出なく、他の回が全て 1 の目が出たという状況です。
このパターンの直積の要素を考えます。

〇 の部分が 1 が出ているという記号でした。
× の部分は、1 以外の 5 通りの可能性があります。
よって、〇〇〇× のタイプだと、
1 × 1 × 1 × 5 = 13 × 5 通り
〇〇×〇 のタイプの場合の数も、同様の考察で計算できます。
× の部分の 5 通りの変化があり、他の成分はすべて 1 となっているので、同じ場合の総数となっていて、13 × 5 通り
〇×〇〇 も同様に、13 × 5 通り
×〇〇〇 も同様に、13 × 5 通り
どのタイプも 13 × 5 通りとなっています。
タイプは、4 回中 3 回の〇が起こるという分け方だったので、13 × 5 通りが、4C3 通り起こり得るということです。
よって、1 の目が 4 回中 3 回出るという条件を満たす場合の数は、4C3×(13 × 5) 通りです。
これと、全事象の要素の個数が 64 通りということから確率を計算すると、
13/63 = (1/6)3 だから、
4C3(1/6)3×(5/6) です。
さらに、5/6 = 1 - 1/6 と書き換えてから、1 乗を (4 - 3) 乗にすると、反復試行の確率の公式の形になります。
4C3(1/6)3×(5/6) =
4C3(1/6)3×(1 - 1/6)4-3
この反復試行の確率について、全事象を表すのに、直積集合が必要になります。
そのため、直積集合を学習していない状況だと、独立試行についての確率の理論を使って、公式が導かれていました。
全事象が明確になると、反復試行の確率の公式の内容の理解が、より深くなるかと思います。
ここからは、独立試行についての内容を述べておきます。
独立試行 :三択クイズの確率
三つの選択肢から一つを選ぶという三択クイズを考えます。
三択のうち、一つだけが正解で、残り二つが不正解という設定です。
1/3 が、この三択に正解する確率ですが、確率を考える上で高校の数学ならではの注意点があります。
どの根元事象も、起こり得る頻度が同じという同様に大使からしいという状況でなければ、確率を定義することができません。
そのため、三択で、二つの不正解を如何にして数学の記号で表すのかということが大切になります。
そこで、×1 と ×2 を二つの不正解とし、それぞれを区別しておきます。
そして、正解を ○ と表すことにします。
このように記号で表すと、三択クイズで選択肢を一つだけ選んだときに、正解したか不正解だったのかということを記号で表現できます。
選択肢を一つ選ぶと、
×1 と ×2 と ○ という 3 通りの可能性があります。
これら三つが、三択クイズで選択肢を一つだけ選ぶという試行における起こり得る場合です。
試行を 1 回だけ行ったとき、×1 と ×2 と ○ のどの一つも同じ割合で出現するという設定で考えます。
これは、×1 と ×2 と ○ の三つの中から、無作為に一つだけを選ぶということです。
そのため、どの場合も出現する割合が同じということです。
起こり得る場合たちを全て集めた集合のことを全事象といいます。
{×1, ×2, ○} が、この三択クイズの試行についての全事象です。
2問ある三択クイズの全事象
1 問目の三択クイズの結果が、正解か不正解に関わらず、2 問目の三択クイズの正解と不正解が同じ頻度で起こるという状況を設定します。
1 回目の試行が、2 回目の試行に影響を及ぼさないという状況です。
この二つの試行が、互いに影響を及ぼさないという状況のことを独立試行といいます。
2 問ある三択クイズの確率を考えたいのですが、独立試行の確率が、どのように定義されているのかということを理解しておくと、独立試行の確率問題を三択クイズに限らず自分で思考できるようになります。
確率ですから、全事象という集合と、その集合に含まれている場合を、どのように定義するのかが大切になります。
先ほどは 1 問しかない三択クイズだったので、それぞれの起こり得る場合を表す記号が比較的にシンプルだったのですが、三択クイズが 2 問あると、順番が絡んできます。
つまり、同じ正解でも、1 問目の三択クイズに正解するのと、2 問目の三択クイズに正解するのを区別しなければなりません。
そこで、記号の表し方を工夫します。
○(1) を 1 問目の三択クイズに正解するということを表す記号とします。
○(2) だと、2 問目の三択クイズに正解するということです。
また、不正解については、一つの問題について、区別した不正解が二つあり、1 問目の不正解と 2 問目の不正解も区別します。
この内容を記号で表すことを考えます。
i を 1 以上 2 以下の自然数とし、
×1(i) と ×1(i) をそれぞれ i 問目に不正解ということを表すことにします。
1 つの問題には不正解が二つあるので、
×2(i) と ×2(i) という記号も用意しておきます。
これで、i が 1 から 2 までの自然数を走ったときに、どのような場合が起きたのかを数学の記号で表すことができました。
×2(1) だと、1 問目の三択クイズで、×2 という不正解を選んだということです。
1 問目で三択から一つの選択肢を選ぶということと、2 問目で三択から一つの選択肢を選ぶということを順番をつけて表すには、座標の組の形で表します。
(×2(1), ○(2)) だと、
1 問目で ×2(1) を選んで不正解で、2 問目で ○(2) を選んで正解するということを表せます。
これらの組が全部で何通りあるのかは、1 問目で 3 通りの選び方があり、2 問目で 3 通りの選び方があるということから、樹形図の考え方で計算できます。
3×3 = 9 なので、全部で 9 通りの組があります。
これら 9 個の組を全て集めてできる集合が、全事象 U となります。
独立試行 :2問ある三択クイズの確率
先ほど、全事象 U に含まれている全ての場合が 9 通りだということを求めました。
これが、「起こり得る場合の総数」です。
条件を満たす確率を計算するときに、条件を満たす場合の総数を 9 で割ることになります。
そこで、1 問目と 2 問目の両方ともで不正解となる確率を求めることを考えます。
1 問目が不正解ということは、×1(1) か ×2(1) を選ぶということになります。
さらに、2 問目も不正解ということなので、×1(2) か ×2(2) を選ぶということになります。
即ち、
(×1(1), ×1(2)), (×1(1), ×2(2)),
(×2(1), ×1(2)), (×2(1), ×2(2)) の 4 通りが、1 問目と 2 問目の両方ともで正解となるという条件を満たす場合になります。
よって、求める確率は、
4 ÷ 9 = 4/9 です。
この確率は、1 問目が不正解で、かつ、2 問目も不正解という論理を集合の要素を用いて考えました。
今度は、「または」という論理を使った条件を満たす確率を考えてみます。
少なくとも一つという論理
1 問目か 2 問目の少なくとも一つで正解する確率を求めます。
少なくとも一つということは、「1 問目または 2 問目で正解をする」ということになります。
数学では、この内容を次の三つのケースとして定めています。
① 1 問目が正解で 2 問目が不正解
② 1 問目が正解で 2 問目も正解
③ 1 問目が不正解で 2 問目が正解
数学で、少なくとも一つが成立するというときは、二つ以上が成立するということも含めて考えます。
そのため、② のケースも条件を満たす場合として考えます。
それでは、① のケースから順に何通りあるのかを調べます。
1 問目が正解で 2 目が不正解というケースなので、
(○(1), ×1(2)), (○(1), ×2(2)) という 2 通りが該当します。
次に ② のケースです。
1 問目が正解で 2 問目も正解ということです。
(○(1), ○(1)) の 1 通りのみとなります。
最後に ③ のケースです。
1 問目が不正解で 2 問目が正解ということです。
(×1(1), ○(2)), (×2(1), ○(2)) の 2 通りが該当します。
これで、1 問目か 2 問目の少なくとも一つで正解するという条件を満たす場合の総数が分かりました。
2+1+2 = 5 より、5 通りです。
起こり得る場合の総数が 9 通りでした。
よって、
5 ÷ 9 = 5/9 が求める確率となります。
同じく 3 問の三択クイズや、一般に n 問の三択クイズの確率を考えることができます。
3問以上の三択クイズ
1 問目、2 問目、3 問目まで三択クイズがあるときを考えます。
各問題の正解と不正解が、他の問題へ影響を及ぼさないという独立試行で考えます。
正解、不正解を順番をつけて記号で表すことが大切になります。
表現をするための発想は、2 問の三択クイズと同じです。
i を、1 以上 3 以下の自然数として、
×1(i), ×2(i), ○(i) と表します。
これで、×2(i) だと、i 問目が不正解というように記号を用いて表すことができました。
次に、全事象という集合を考えたいところです。
順番も含めて記号で表したいので、組で考えます。
1 問目が ×2(1) で不正解、2 問目が ○(2) で正解、3 問目が ○(3) で正解という場合だと、三つの要素を用いた組で表します。
(×2(1), ○(2), ○(3)) という組で、この内容を表すことができます。
三つの要素を用いた組を全て集めた集合を 3 問の三択クイズの全事象とします。
この全事象に全部で何通りの場合が含まれているのかを樹形図の考え方で計算します。
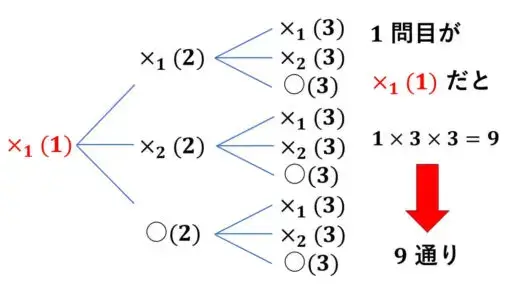
1 問目が x1(1) のとき、このような樹形図の分岐が起こり、9 通りの場合が得られます。
1 問目が x2(1) や ○(1) のときにも、全く同じ分岐が発生します。
そのため、
3 × 9 = 27 より、27 通りの場合が起こり得る場合の総数となります。
これで、3 問ある三択クイズについての全事象に含まれる場合の総数を求めることができました。
(□, ◇, △) という組で、それぞれの部分に 3 通りの場合が配置されるということになります。
そのため、33 = 27 通りというわけです。
さらに、一般化して文字を用いて n 問ある三択クイズの全事象に含まれる場合の総数を考えます。
n問ある三択クイズの全事象
各問題の正解と不正解が、他の問題へ影響を及ぼさないという独立試行で考えます。
1 問目から順に n 問目まで三択クイズがある状況です。
i を、1 以上 n 以下の自然数として、
×1(i), ×2(i), ○(i) と表します。
(□, … , △) という組で起こり得る場合を表します。
3 通りの場合を n ヶ所に配置するという樹形図の発想で、これらの組をすべて集めた集合である全事象に含まれる場合の総数を計算します。
3 を n 個で掛け算をすると、全事象に含まれる全ての組の総数となります。
すなわち、3n 通りが起こり得る場合の総数です。
この記事では、独立試行について、全事象を見える化して述べてきました。
n 個の独立試行で、1 回の試行が、どれも同じになっているときに反復試行といいました。
この記事で扱った反復試行の確率の内容は、数学Bの二項分布につながります。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。