テンソル積 | 普遍性に関するバランス写像の定理【右R加群と左R加群で】

" テンソル積 “についての定義と、備えているバランス写像についての定理を解説します。
右 R 加群と左 R 加群についての R 上のテンソル積の数学における内容になります。
普遍性は、バランス写像についての定理の内容を満たす写像を備えている他の加群があったとすると、テンソル積とZ-加群として同型というものです。
数学科で学習する加群のテンソル積は、ある剰余加群のことです。
剰余について環論の入門で学習した内容の例を先に述べます。
テンソル積 :手頃な剰余の例から定義へ
R を実数全体とし、
R[x] を R 係数の多項式環とします。
x2 + 1 で生成されるイデアルを
(x2 + 1) と表します。
剰余環 R[x]/(x2 + 1) の元を
[f(x)] (f(x) ∈ R[x])と表します。
x2 + 1 は、割っているイデアルの元なので、
[x2 + 1] = [0]
両辺に [-1] を加えると、
[x2] = [-1]
これがテンソル積の定義を理解するために必要な剰余についての知識です。
■ 割ったイデアルに含まれている元を代表元とすると、それは剰余環における零元ということ。
■ その零元に等しい等式において、移項をすると関係式ができるということです。
余談ですが、剰余環 R[x]/(x2 + 1) における得られた関係式は、[x] と [x] の積が乗法単位元となるということです。
そのため、この剰余環は複素数体と体として同型になっています。
この内容を踏まえて、テンソル積の定義を解説します。
ただし、環 R は可換環で乗法単位元 1 をもっているものとし、整数環を Z と表します。
加群のテンソル積
M を 右 R 加群、N を左 R 加群とします。
このとき、直積集合 M × N を基底とする Z-自由加群をZ(M, N) と表します。
Z(M, N) は、M × N を基底とする自由加群のことです。
Z(M, N) の元は、
Σi zi(xi, yi) (zi∈Z, xi∈M, yi∈N) という形式的に、整数 zi を直積集合の元の前に置いたものたちの有限和です。
有限個の zi を除いて、前に置いている整数は 0 ということが、有限和です。
ここで、Z(M, N) について、次の元たちで生成される部分加群をW(M, N) と表すことにします。
<W(M, N) の生成元たち>
(x1+x2, y)-(x1, y)-(x2, y),
(x, y1+y2)-(x, y1)-(x, y2),
(xr, y)-(x, ry)
(ただし、∀x, x1, x2∈M, ∀y, y1, y2∈N, ∀r∈R)
これらの形の Z(M, N) における元たちを含んだ部分加群すべての共通部分が、生成される部分加群です。
全体 Z(M, N) 自信は、これらの元たちをすべて含んでいる部分加群なので、
W(M, N) は定義可能です。
次に、W(M, N) で割って、
Z(M, N)/W(M, N) という剰余加群を定義します。
実は、この剰余加群が M と N の R 上のテンソル積です。この剰余加群のことを、サムネイルの画像に書いていたテンソル積の独特の記号で表します。
※ 加群の定義という記事で、部分加群や剰余加群の基礎的なことを解説しています。
Z(M, N)/W(M, N) は、記号が長いので、T と表すことにします。
ここで、先ほど述べた、剰余をとったときの一般論を使います。生成元たちは部分加群の元なので、剰余加群における零元 [0] となっています。
そして、移項をすると、剰余加群における関係式が得られるということです。
テンソル積 :基礎となる関係式
剰余加群 T において、
[(x1+x2, y)-(x1, y)-(x2, y)] は零元 [0] です。
つまり、
[(x1+x2, y)-(x1, y)-(x2, y)] = [0]
両辺に [(x1, y)] + [(x2, y)] を加えると、
[(x1+x2, y)]
= [(x1, y)] + [(x2, y)] … (1)
[(x1+x2, y)] のことを、(x1+x2) と y の真ん中にテンソルのバツ印をつけたものが、一般的なテンソルの表し方になります。
数学における加群のテンソル積の定義は、Z-自由加群と剰余加群という代数学入門で学習した内容を使ってシンプルにつくられています。
この要領で、理解を広げるために、まだテンソルの記号は使わずに、剰余加群についての記号のままで議論を進めます。
他の関係式も書いておきます。
[(x, y1+y2)-(x, y1)-(x, y2)] は剰余加群 T における零元 [0] なので、先ほどと同様に移項をすると、
[(x, y1+y2)]
= [(x, y1)]+[(x, y2)] … (2)
残りのタイプの生成元についても、同様のことをします。
[(xr, y)-(x, ry)] が剰余加群における零元なので、移項をすると、
[(xr, y)] = [x, ry] … (3)
これで、テンソル積における関係式ができました。
では、ここまでの内容をテンソル積の記号を使ってまとめます。
(1) から (3) の関係式をテンソルの記号で述べたものです。
特に分かること
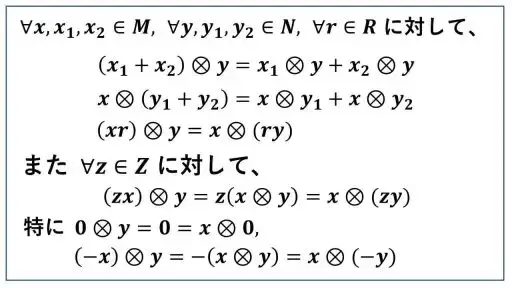
上から三つの等式は、先ほど導いた (1) から (3) の関係式です。
アーベル群を学習したときに、同じ元を有限個で加法を計算するという内容が出てきます。
これと、(1) と (2) の関係式を合わせると、中段の式が得られます。
練習のために、この中段の式を解説します。
x ∈ M を繰り返し n 個足す(n は自然数)ということを nx とする考え方です。
0x は 0 のことで、n が負の整数のときは、
-x を |n| 個足すということです。
そのため、任意の整数 z と任意の x ∈ M について、zx という Z からの作用を考えることができます。
N についても、この Z からの作用が定義されています。
(1) について、[zx, y] = z[x, y]
(2) について、[x, zy] = z[x, y]
よって、
[zx, y] = z[x, y] = [x, zy]
これをテンソルの記号を使って表したものが、中段の式です。
図において、「特に」と書いている内容は、z として 0 と -1 のときを述べているだけです。
これで、テンソル積についての基礎となる関係式が得られました。このブログ記事は、剰余加群についての入門的な考察だけで、議論を進めます。
ここまでの内容で、剰余加群をテンソル積と定義しましたが、テンソル積が自明なものとなってしまうことも起こり得ます。
Z(M, N) と W(M, N) が一致していて、
T = Z(M, N)/W(M, N) が零元のみの自明な加群となってしまうこともあります。
確実にテンソル積をとったときに、自明にならないときというと、M と N が自由加群となっているときが挙げられます。
M と N が自由加群のときは、M の基底と N の基底のテンソルが、テンソル積の基底となります。
物理でお馴染みの m 次元と n 次元の線形代数のテンソルだと、体上のベクトル空間の右作用を左作用と考え、mn 次元の線形代数となっています。
そのため、自明ではないということになります。
では、使う記号を剰余加群についての内容のものにしておき、普遍性を入門的な集合論の内容で押さえます。
テンソル積 :バランス写像
【定義】
右 R 加群 M と左 R 加群 N に対して、
直積 M × N から加法群 G への写像 f で、次を満たすものをバランス写像という。
∀x, x1, x2∈M, ∀y, y1, y2∈N, ∀r∈R に対して、
f((x1+x2, y)) = f(x1, y) + f(x2, y),
f(x, y1+y2) = f(x, y1) + f(x, y2),
f(xr, y) = f(x, ry)
先ほど定義したテンソル積は、バランス写像を備えています。このテンソル積が備えるバランス写像が、どう定義されているのかを示します。
バランス写像の定義の G として、
T = Z(M, N)/W(M, N) とします。
M × N という直積集合を基底とする
Z-自由加群 Z(M, N) の元は、
Σi zi(xi, yi) (zi∈Z, xi∈M, yi∈N) という形の有限和でした。
そのため、テンソル T の元は、
[Σi zi(xi, yi)] = Σi zi[(xi, yi)] という有限和の形です。
このことを考えて、M × N から T へのバランス写像を定義することを考えます。
まず、M × N から Z(M, N) への次のような写像 i を考えます。
任意の (x, y) ∈ M × N に対して、
i(x, y) = (x, y) となっています。
次に Z(M, N) から剰余加群 T (テンソル積)へは、自然な加群準同型 k を考えます。
つまり、
k(Σi zi(xi, yi))
= [Σi zi(xi, yi)] = Σi zi[(xi, yi)]
合成写像 k・i のことを π と表すことにします。この π がバランス写像の定義を満たします。
∀x, x1, x2∈M, ∀y∈N に対して、
π((x1+x2, y))
= k・i((x1+x2, y))
= k((x1+x2, y))
= [x1+x2, y] = [x1, y] + [x2, y]
一方、
π(x1, y) = k・i(x1, y)
= k(x1, y) = [x1, y]
同様に、π(x2, y) = [x2, y]
よって、
π((x1+x2, y)) = π(x1, y) + π(x2, y)
残りの条件ついても、定義通りに写像の対応を書き出すと、
π(x, y1+y2)
= π(x, y1) + π(x, y2),
π(xr, y) = π(x, ry) が得られます。
このバランス写像 π についての普遍性についての定理を証明します。
上で述べた加法群は、Z-加群ということも使います。
普遍性に関する定理
【普遍写像性質の定理】
M を右 R 加群、N を左 R 加群とする。
G を任意の加法群とし、
f : M × N → G を任意のバランス写像とする。
このとき、テンソル積 T から G への Z-準同型写像 f* が、ただ一つ存在し、f*・π = f となる。
<証明>
与えられた f を用いて、
f’ : Z(M, N) → G を次のように定義します。
Σi zi(xi, yi) ∈ Z(m, N) に対して、
f'(Σi zi(xi, yi)) = Σi zif((xi, yi))
自由加群 Z(M, N) における加法について、
zab(a, b) と zcd(c, d) が、
a = c かつ b = d となっているときに、
zab(a, b) + zcd(c, d)
= (zab + zcd)(a, b) となることから、f’ は Z-準同型写像となっています。
f がバランス写像であることから、
W(M, N) ⊂ ker f です。
なぜなら、W(M, N) の生成元を f で移すと 0 になるからです。
例えば、
f((x1+x2, y)-(x1, y)-(x2, y))
= f((x1+x2, y))-f((x1, y))-f((x2, y)))
ここで、バランス写像の定義から、
f((x1+x2, y)) = f(x1, y) + f(x2, y) なので、
f((x1+x2, y)-(x1, y)-(x2, y)) = 0 となります。
他のタイプの生成元についても同様です。
W(M, N) ⊂ ker f’ なので、f’ と自然な準同型写像を用いて、
π* : T = Z(M, N)/W(M, N) → G が定義できます。
つまり、
f*([x]) = f'(x) ([x] ∈ T)
もし、[x] = [y] (x, y ∈ Z(M, N)) だとすると、
ある u ∈ W(M, N) が存在し、x = y + u
W(M, N) ⊂ ker f’ だから、
f'(x) = f'(y + u)
= f'(y) + f'(u) = f'(y)
よって、f* は代表元の取り方に依らずに定義できています。
そして、f’ が Z-準同型写像なので、f* も Z-準同型写像です。
任意の (a, b) ∈ M × N に対して、
i((a, b) = (a, b) ∈ Z(M, N) でした。
そして、自然な準同型写像 k と i を合成写像である k・i が π でした。
(a, b) ∈ Z(M, N) について、f’ の定義から、
f'((a, b)) = f((a, b)) なので、
f’・i((a, b)) = f'((a, b)) = f((a, b))
よって、f’・i = f
これより、
任意の (c, d) ∈ M × N に対して、
f*・k・i((c, d)) = f*・k((c, d))
= f*[(c, d)] = f'((c, d)) = f((c, d))
したがって、f*・k・i = f
ゆえに、k・i = π だったので、
f*・π = f となります。
次に、ただ一つであることを示します。
T から G への Z-準同型写像 g が存在して、
g・π = f を満たしていたとします。
すると、
任意の (x, y) ∈ M × N について、
π ((x, y)) = [x, y] ∈ T だから、
g([x, y]) = g・π([x, y])
= f((x, y))
= f*・π((x, y)) = f*((x, y))
g と f* は、Z-準同型写像であり、
T の元は、
Σi zi[ci, di] ((ci, di)∈M×N) という形だから、
g(Σi zi[ci, di]) = Σi zig([ci, di])
= Σi zif*([ci, di]) = f*(Σi zi[ci, di])
よって、T の各元について、対応先が等しいことから、g = f*【証明完了】
この定理から、普遍性が導かれます。
普遍性について
Z-加群 T’ は次の①と②を満たすとする。
① M × N から T’ へのバランス写像 π’ が定義されている。
② G を任意の加法群とし、
f : M × N → G を任意のバランス写像とするとき、
f*・π’ = f を満たす f* が、ただ一つ存在する。
このような π’ を備えた T’ は、必ず T と Z-加群として同型になるということがテンソル積の普遍性です。
※ 補足説明という記事の段落「他の記事の証明1」で証明を述べています。
【関連する記事】
● 多項式環の不定元
● 直和空間(テンソルと直和の関係)
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。