環準同型写像 | 単射とker f = {0}は同値など
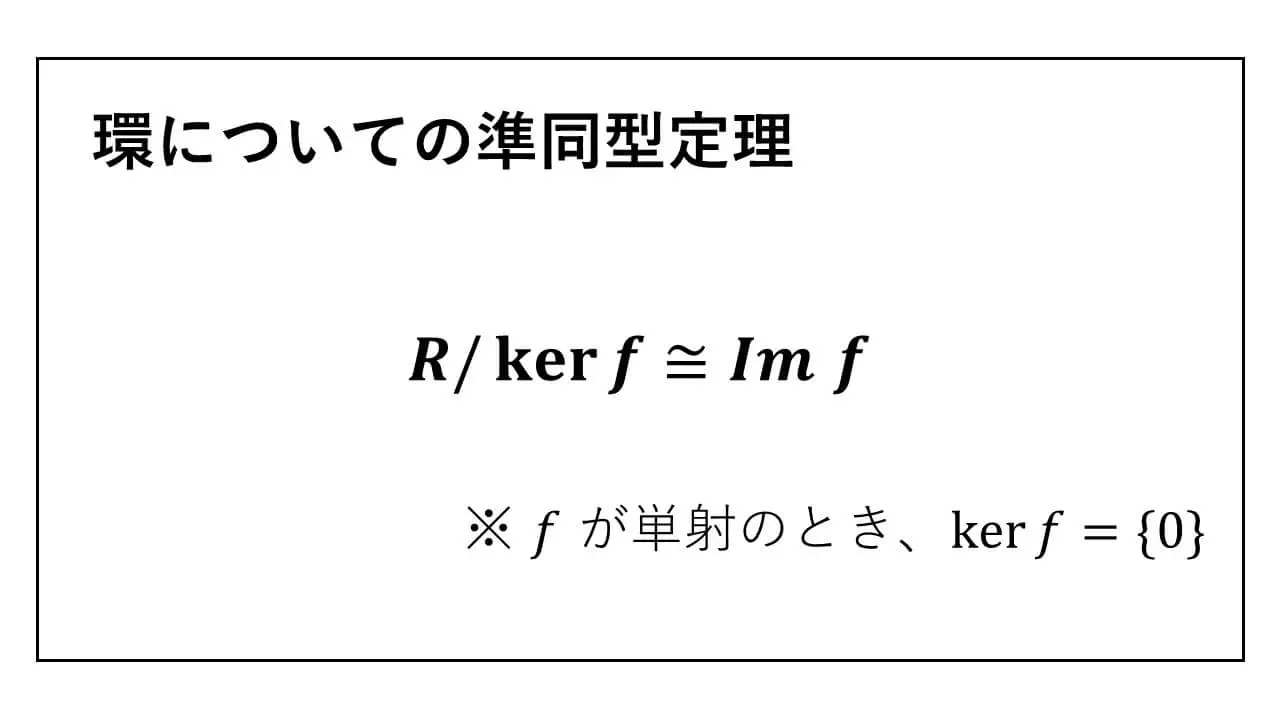
環準同型写像 f は、ker f = {0} であることと、単射であることが同値です。
そのため、体から体への環準同型写像は、必ず単射となることが導けます。
この記事では、環準同型写像についての ker を考え、準同型定理を示します。
それでは、環についての準同型写像の定義から説明します。
環準同型写像 : 定義
【定義】
環 R1 から環 R2 への写像 f が準同型写像であるとは、次の①から③を満たすことである。
任意の a, b ∈ R1 に対して、①と②が成立。
① f(a + b) = f(a) + f(b)
② f(ab) = f(a)f(b)
さらに、1 ∈ R1 の f による像は、R2 の乗法についての単位元となる。
③ f(1) = 1
これが、環準同型写像の定義です。
可換体の準同型写像を以下で議論します。
先ほど環について述べた準同型写像の定義は、体としての準同型写像の定義にもなります。
体の場合は、この定義から、次のことが導けます。
環準同型写像と体
【命題】
f を体 F から体 K への写像とし、任意の a, b ∈ F に対して、
f(a + b) = f(a) + f(b), f(ab) = f(a)f(b) とする。
また、Im f ≠ {0} とする。
このとき、任意の x ∈ F - {0} に対して、
f(x-1) = f(x)-1 となる。
<証明>
任意の x ∈ F - {0} について、x は 0 でないので、体の定義から、乗法に関する逆元が存在します。
それが x-1 です。
ゆえに、xx-1 = 1
f で移すと、f(xx-1) = f(1) = 1
※ 定義③より f(1) = 1
定義②より、f(x)f(x-1) = f(xx-1)
よって、f(x)f(x-1) = 1 … ★
ここで、f(x) ∈ K が 0 だとすると、0 と f(x-1) との乗法の値が 0 となってしまうので、★の計算結果と矛盾します。
よって、背理法から、f(x) は 0 ではありません。
したがって、f(x) ∈ K - {0} なので、体の定義から、乗法に関する逆元 f(x)-1 が存在します。
この f(x)-1 を★の両辺に左から乗じると、
f(x)-1(f(x)f(x-1)) = f(x)-1
結合律より、
(f(x)-1f(x))f(x-1) = f(x)-1
f(x)-1f(x) = 1 より、
f(x-1) = f(x)-1【証明終了】
単射についての定理の証明
【定理】
F, K を体とし、
f : F → K を環準同型写像とする。
このとき、
ker f = {0} である。
<証明>
0 ∈ F について、
f(0) = f(0 + 0) より、f(0) = 0
よって、0 ∈ ker f
次に、ker f には、0 でない F の元が含まれていないことを背理法で示します。
x ∈ ker f が、もし 0 でなかったと仮定します。
そうすると、体の定義から、x の乗法逆元 x-1 が存在します。
1 = xx-1 なので、
f(1) = f(xx-1) = f(x)f(x-1) … ★
x ∈ ker f より、
f(x) = 0 なので、
★の右辺が 0 となり、f(1) = 0
一方、
環準同型写像の定義から、f(1) = 1
ゆえに、1 の f による像が異なる二つの値を取ってしまったので、写像 f の 一対一対応に矛盾しました。
背理法より、ker f には、0 でない F の元は存在しないことになります。【証明終了】
【補足】
示したことは、f が単射ということを意味しています。
実際、f(a) = f(b) (a, b ∈ F) とすると、
f(a - b) = f(a) - f(b) = 0
よって、a - b ∈ ker f = {0} となり、
a - b = 0 です。
すなわち、a = b なので、f が単射ということになります。
逆に、
体に限らず環を定義域とする環準同型写像 f が単射であれば、
ker f = {0} となります。
※ f(0) = 0 より、0 でない元の f による像は 0 でない元となるからです。
環準同型写像について、単射であることと、kernel が {0} ということが同値になります。
環についての準同型定理
準同型写像が単射でないとき、
つまり、ker f に 0 以外の元があるとき、次の準同型定理が基本になります。
簡単のため、以下の R と R’ は乗法単位元をもつ可換環とします。
I ⊂ R が加法群として R の部分群で、
任意の r ∈ R と任意の a ∈ I に対して
ra ∈ I となっているときに、I を R のイデアルといいます。
ker f は R のイデアルとなっています。

<証明>
R において、x, y ∈ R が x - y ∈ ker f となっているときに、
x ~ y と二項関係 ~ を定義します。
この二項関係 ~ は、反射律、対称律、推移律を満たし、R 上の同値関係となっていることが分かります。
同値関係 ~ によって、R を類別し、
すべての同値類を集めた集まりを
R/ker f と表します。
各同値類は、x + ker f (x ∈ R) という形です。
φ : R/ker f → R’ を
φ(x + ker f) = f(x) と定義します。
この φ は同値類の代表元の取り方に依らないで定義できている (well-defined) ということは、次のようにして示されます。
x + ker f = a + ker f だとすると、
同値関係 ~ の定義から
x - a ∈ ker f となります。
そのため、ある s ∈ ker f が存在し、
x - a = s
つまり、x = a + s です。
f は 準同型写像なので、
f(x) = f(a + s) = f(a) + f(s) です。
また、s ∈ ker f なので、f(s) = 0 だから、
f(x) = f(a + s) = f(a)
よって、
φ(x + ker f)
= f(x) = f(a) = φ(a + ker f)
これで、φ が代表元の取り方に依らずに定義できていることが示せました。
R/ker f における加法と乗法はそれぞれ、x, y ∈ R に対して、次のように定義されていて、環の定義を満たします。
今、R が可換環なので、R/ker f も可換環です。
(x + ker f) + (y + ker f)
= (x + y) + ker f ,
(x + ker f)(y + ker f)
= (xy) + ker f
※ これら加法と乗法も well-defined であることは、後で説明します。
R が可換環なので、
(x + ker f)(y + ker f)
= (xy) + ker f
= (yx) + ker f
= (y + ker f)(x + ker f)
となり、R/ker f も可換環ということが分かります。
R/ker f の加法と乗法の定義から、
0 + ker f が加法についての零元で、
1 + ker f が乗法についての単位元ということが分かります。
この剰余環 R/ker f の加法と乗法の定義から、φ が全射準同型写像となっていることを示します。
仮定より、f が全射なので、
任意の r’ ∈ R’ に対して、x ∈ R が存在して、
f(x) = r’
よって、x を含む同値類 x + ker f を φ で移すと、
φ(x + ker f) = f(x) = r’
これで、φ が全射であることが示せました。
φ が環準同型写像であることを次に示します。
x, y ∈ R に対して、
φ((x + ker f) + (y + ker f))
= φ((x + y) + ker f)
= f(x + y) = f(x) + f(y)
= φ(x + ker f) + φ(y + ker f)
次に乗法についてです。
φ((x + ker f)(y + ker f))
= φ((xy) + ker f)
= f(xy) = f(x)f(y)
= φ(x + ker f)φ(y + ker f)
これで、準同型写像であることが示せました。
環として同型写像であることを示したいので、φ が 単射であることを示す必要があります。
今、φ が環としての準同型写像であることが示せました。
上で述べたことから、
準同型写像 φ が単射であることは、
ker φ が R/ker f の零元 0 + ker f のみからなることと同値です。
φ(0 + ker f) = f(0) = 0 なので、
0 + ker f ∈ ker φ
他に ker φ の元が無いということを示します。
x + ker f ∈ ker φ とすると、
ker φ の定義から
φ(x + ker f) = 0 ∈ R’
また、φ の定義から
φ(x + ker f) = f(x)
そのため、f(x) = 0 ∈ R’
ker f の定義から、x ∈ ker f
ker f は加法群ですから、
x - 0 ∈ ker f なので、同値関係 ~ の定義より、
x + ker f = 0 + ker f
したがって、
ker φ = {0 + ker f} が示せました。
準同型写像 φ について、ker φ が R/ker f の零元のみから成るので、φ は単射です。
これで、R/ker f が R’ と同型であることが示せました。【証明完了】
※ 第二同型定理という記事で、群についての準同型定理を解説しています。
この証明では、f が全射であることが仮定されていました。
f が全射であろうがなかろうが、R から Im f へは全射になるので、R’ として Im f を考えると、同様の証明で、R/ker f と Im f が環として同型になるということが成立します。
先ほどの証明では飛ばしていましたが、
R/ker f における加法と乗法が、それぞれ矛盾なく定義できていることを確認します。
代表元の取り方に依らない
R/ker f 上の二項演算は、
直積 R/ker f × R/ker f から R/ker f への写像です。
加法も乗法も、写像として一対一対応をしています。
しかも、代表元の取り方に依らない写像となっています。
この代表元の取り方に依存しない写像となっていることを
well-defined といいます。
x, y ∈ R について、~ について、x と y を含む同値類をそれぞれ S(x) と S(y) としたときに、直積の元として、
(S(x), S(y)) ∈ R/ker f × R/ker f を考えます。
この直積の元に対して、
x + y を含む同値類 S(x + y) を対応させる写像が R/ker f における加法ということです。
この対応が well-defined であることを確認するときに、同値類を先ほどの x + ker f という形で表した方が扱いやすいです。
この x ∈ R のことを同値類 S(x) の代表元といいます。
S(x) から他の元 a を、S(y) から他の元 b をとってきたときに、S(x) = S(a), S(y) = S(b) となっていることは集合論の一般論で分かっています。
ただし、
(S(x),S(y))=(S(a),S(b))∈R/ker f × R/ker f について、
加法としようとしている対応が、
本当に S(x + y) = S(a + b) となっているのかは、確認する必要があります。
つまり、
x+ker f=a+ker f かつ y+ker f=b+ker f のときに、
(x + y) + ker f = (a + b) + ker f となっているのかということを示すということです。
ここで、同値関係 ~ の定義と、ker f が加法群であることが効いてきます。
x ~ a かつ y ~ b なので、
x-a ∈ ker f かつ y-b ∈ ker f
ker f は加法群ですから、
ker f ∋ (x - a) + (y - b)
= (x + y) - (a + b)
~ の定義から (x + y) ~ (a + b) なので、
(x + y) と (a + b) は同じ同値類に含まれていることが分かりました。
そのため、S(x + y) = S(a + b)
記号を書き換えると、
(x + y) + ker f = (a + b) + ker f です。
これで、加法について well-defined であることが示せました。
次に、乗法について示します。
(S(x), S(y)) に対して、S(ab) を対応させる写像が R/ker f の乗法です。
x+ker f = a+ker f かつ y+ker f = b+ker f のとき、
(xy) + ker f = (ab) + ker f となることを示します。
x - a ∈ ker f かつ y - b ∈ ker f なので、
ある s, t ∈ ker f が存在し、
x = a + s, y = b + t と表すことができます。
よって、
xy = (a + s)(b + t)
= ab + (at + sb + st)
s, t はイデアル ker f の元なので、
at, sb, st ∈ ker f です。
※ R は可換環より、sb ∈ ker f です。
ker f は加法群なので、
at + sb + st ∈ ker f だから、
ab + (at + sb + st)
∈ ab + ker f
よって、xy ∈ ab + ker f = S(ab)
xy が ab を含む同値類に含まれていることが示せたので、
S(xy) = S(ab) です。
これで、乗法についてもwell-defined であることが示せました。
【関連記事】
■ ファイ関数
■ イデアルの積
■ 加群の定義
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。