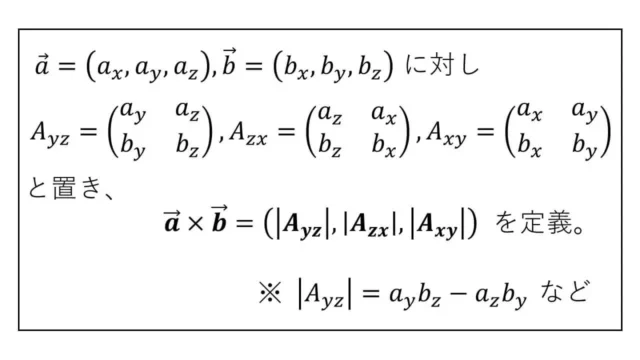高校数学 単元一覧 | 数学Cが復活した学習過程
高校数学で数学Cが復活しました。それに伴って、" 高校数学 単元一覧 “を作り直しました。
このページに、今まで投稿した高校数学の記事を全てまとめています。
単元別に記事を配置しています。ただし、旧課程の整数分野については、今後も有名な大学で出題されると思いますので、残しています。
数学IAの記事から順に配置しています。
高校数学 単元一覧 :数学IA
【数学I】
数と式、図形と計量、二次関数、データの分析という単元についてのブログ記事を投稿しています。
■ 数と式の単元
・三乗和の公式
・複二次式(平方差)
・二重根号の外し方
・絶対値(関数のグラフ)
・連立不等式
論理規則と集合は、あらゆる単元で使われます。
・要素(元)∈(部分集合も)
・共通部分と和集合
・命題-仮定-結論
・必要条件-十分条件(後半は大学の行列で)
■ 二次関数
・平方完成(基本形)
・軸と定義域(場合分け)
・解の存在範囲(二次方程式)
■ 図形と計量
・外接円(辺の垂直二等分線)
・正弦定理(三角比)
・三平方の定理(余弦定理)
■ データの分析
・四分位数(中央値から)
・分散(標準偏差/変量変換)
【数学A】
場合の数と確率、図形の性質についてのブログ記事になります。
■ 場合の数と確率
・補集合(差集合/ドモルガンの法則)
・個数定理(3つの集合も)
・組合せの公式証明(nCr)
・同じものを含む順列(最短経路)
・同様に確からしい【確率】
・じゃんけんの確率
・反復試行の確率
・条件付き確率
■ 図形の性質
・三角形の面積比(チェバの定理)
・平行線と線分の比(メネラウスの定理)
・方べきの定理
・トレミーの定理
・オイラーの多面体定理(展開図も)
・二つの円の位置関係
また、情報についての記事も投稿しています。
・情報量-ビット
・2進数-補数
・16進数-変換
・5進数の小数
・浮動小数点数(バイアス)
次は、高校から大学へのつなぎになる内容の記事たちです。
旧課程から残している記事
整数分野は、新課程、旧課程に関わらず、これまでも多くの有名な大学で出題されていることから、記事を残しています。また、大学数学の代数分野の環論の入門に良い練習ともなるかと思います。
・素数判定法(エラトステネスの篩)
・4の倍数(見分け方)
・連続整数の積(n!の倍数)
・3の倍数判定法(証明)
・7の倍数判定法(11の倍数も)
・部屋割り論法(鳩の巣論法)
・無限降下法(植木算を証明)
・余り-整数問題
・素因数の個数(末尾の0)
・最大公約数-求め方
・n乗の差(an-bnの公式)
・中国剰余定理
・互除法(ユークリッド)
・一次不定方程式
・合同方程式の解き方
・フェルマーの小定理
・メビウスの反転公式(メビウス関数)
・ファイ関数(オイラー)
次は、数学IIBの記事たちです。
高校数学 単元一覧 :数学IIB
【数学II】
いろいろな式と図形と方程式、そして微積分についての記事を、投稿しています。
・不等式の証明(絶対値アリ)
・恒等式(方程式との違い)
・定点を通る直線(恒等式の実践)
・解と係数の関係(2変数)
・3変数の対称式
・虚数と複素数の違い
・複素数の除法(逆数)
・複素数の相等(等しい)
・二直線が垂直(傾きの積-1)
・指数方程式
・真数と底(対数の定義)
・底の変換公式
・対数方程式
・常用対数(小数首位の数)
・弧度法(弧の長さからラジアン)
・半角の公式(倍角の公式から)
・和積変換公式(積和変換も)
・3倍角の公式(4倍角も)
・増減表(一部に数学IIIの定理を使用)
・偶関数 – 奇関数(定積分)
・1/6公式【なぜマイナスか】(接点と重解)
・合同な放物線【面積比】
三角関数、指数関数、対数関数についての記事は、今のところ大学の複素解析の内容のブログ記事として投稿しています。
【数学B】
統計的な推定、数列についての記事です。
・相関係数(-1≦r≦1)
・期待値E(X)(確率変数)
・二項分布(離散的)
・同時分布(E(aX+bY))
・確率変数の独立(E(XY),V(X+Y))
・等差中項(二数の和)
・等差数列のグラフ
・調和数列(逆数をとると)
・等比数列の和(公式の証明)
・シグマ記号(項たちの和)
・階差数列(シグマの利用)
・第n項までの和(Sn-Sn-1)
・4乗のシグマ(Σk4, Σk5の式)
・特性方程式(なぜ同じ文字)
・フィボナッチ数列
・一次分数型の漸化式
・連立漸化式(係数比較の謎)
次は数学IIICについての記事です。
高校数学 単元一覧 :数学IIIC


【数学III】
極限、微積分についてのブログ記事を投稿しています。
・はさみうちの定理(関数の極限)
・ロルの定理(平均値の定理も)
・ロピタルの定理(不定形を解消)
・中間値の定理(使い方と大学の証明)
・ネイピア数(e の定義)
・積の微分(商の微分も)
・合成関数の微分(公式の証明と練習)
・三角関数の微分(sin x の微分など)
・対数関数の微分(対数微分法も)
・媒介変数の微分(サイクロイドなど)
・加速度ベクトル(瞬間の速度)
・等速円運動(角速度)
・置換積分(公式の導出)
・部分積分(漸化式との融合問題も)
・相加相乗平均(数IIIの微分で)
【数学C】
ベクトルの記事が多いですが、一次変換を表す行列の記事も置いておきます。
・内積の定義【平面ベクトル】
・円の接線の方程式
・方向ベクトル-法線ベクトル
・点と直線の距離の公式(証明)
・二次曲線(接線)
・空間ベクトル【平面に垂直なベクトル】
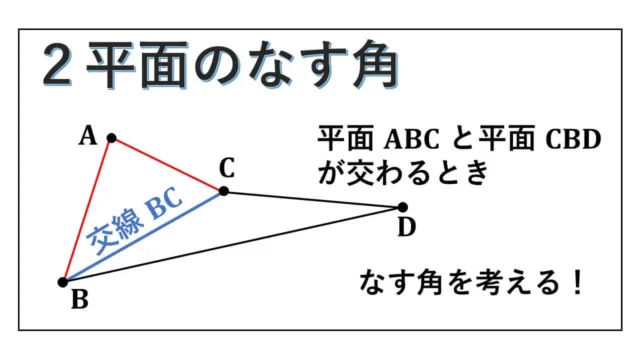
・2平面のなす角(三垂線の定理も)
・ヘロンの公式
・分点公式(内分・外分)
・重心-ベクトル(三角形)
・内心-外心(位置ベクトル)
・垂心-ベクトル(図形の証明も)
・傍心(傍接円の中心)
・チェバの定理の逆(図形とベクトル)
・アポロニウスの円
・外積
複素数平面の極形式に関連する 1 の原始 n 乗根についての内容は、大学数学の円分多項式の内容に踏み込んでいます。
・ド・モアブルの定理(マイナス乗も)
・1の3乗根(ω オメガ)
・累乗根(n乗根)
・円分多項式は整数係数
※ 大学数学へのつなぎの意味で、行列についての記事を置いています。
<線形変換を表す行列>
・Reflection-鏡映(対称変換)
・微分作用素(d/dx)
上の記事たちが、高校数学、もしくは高校から大学の数学への橋渡しを考えて投稿したブログ記事たちになります。