重心 – ベクトル | 三角形の重心を位置ベクトルで表示する【証明】

2024年1月6日

三角形の" 重心 “を位置ベクトルで表示し、公式を導出します。

平面図形について知っている知識を利用して、ベクトルで内容を表現するのに良い練習になるかと思います。

三角形ABCの重心 G について、図形的な内容を先にまとめてから、その内容をベクトルで表します。

その後で、三角形の三つの頂点を表す座標が与えられているときに、重心の座標を表す数IIの公式にも言及しています。

それでは、図形についての基礎知識から述べます。

重心 – ベクトル :図形の知識

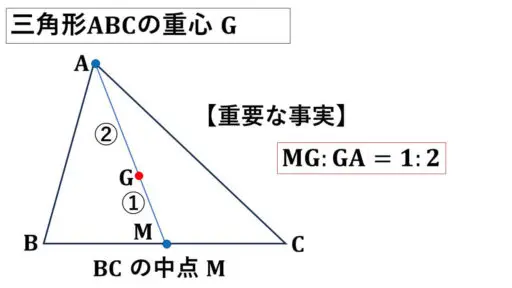
三角形ABCの重心を G とします。

頂点 A の対辺である辺BC の中点を M とします。

中点なので、
BM : MC = 1 : 1 となっています。

ここで、押さえておきたい三角形の重心についての図形的な知識です。

MG : GA = 1 : 2 です。

中点と重心を結んだ線分MG の長さの 2 倍の長さが、重心と頂点を結んだ線分GA の長さになります。

この事実は、三角形の重心が出てきたときに、使う頻度が高いので、しっかりと押さえておくと良いかと思います。

一般的な事実について

三角形の重心なので、各辺の中点と向かい合う頂点を結んだ線たちが交わる 1 点 G についての内容を先ほど述べました。

一般に 1 : 1 以外の分点比について、重心を一般化して交わる 1 点をベクトルで表示することができます。

その交わる 1 点と頂点を結んだ線と、1 点と辺の内分点を結んだ線分の長さについての比も分かっています。

この内容は、チェバの定理の逆という記事で解説をしています。

今回は、三角形の重心に焦点を当てているため、この一般化した内容については、これ以上は触れずに議論を進めます。

それでは、ここからは、ベクトルを使います。

重心 – ベクトル :位置ベクトル表示

点 A, B, C のいずれとも異なる点を O とし、O を位置ベクトルの基準（始点）として、A, B, C を位置ベクトルで表します。

A, B, C の順に位置ベクトルを a→, b→, c→ と表します。

辺BC の中点 M は、
BM : MC = 1 : 1 でした。

そのため、分点比の公式から、
点 M の位置ベクトル m→ を表すことができます。

m→ = 1/2(b→+c→) となります。

次に、ベクトルの減法を用いた式を用意します。

ベクトルMA は、
a→－m→ と、減法を用いて位置ベクトルで表せます。

また、G の位置ベクトルを g→ とすると、
ベクトルMG は、
g→－m→ となります。

この線分の両端点についての減法を用いた位置ベクトルの表し方は、ベクトルを学習し始めたときに出てきますが、平面でも空間でも、よく使うので大切です。

ここで、スカラー倍についての考察も合わせます。

スカラー倍で伸縮

重心についての図形の性質から、
MG : GA = 1 : 2 でした。

そのため、
MG : MA = 1 : 3 です。

つまり、線分MG の長さは、線分MA の長さの 1/3 となっています。

そして、ベクトルMG ベクトルMA は始点が揃っています。

そのため、ベクトルMA を 1/3 でスカラー倍して長さを縮小すると、ベクトルMG に一致します。

それぞれのベクトルを先ほど位置ベクトルで表していたので、位置ベクトルの記号を使い、1/3 の縮小についての内容を等式とします。

g→－m→ = 1/3(a→－m→) となります。

さらに、ベクトルの計算を進めると、
g→ = a→/3+2m→/3 …(1)

ここで、辺BC の中点 M の位置ベクトル表示を思い出します。

すると、
m→ = 1/2(b→+c→) でした。

この両辺を 2 でスカラー倍し、
2m→ = b→+c→ …(2)

(2) を (1) に代入すると、
g→ = a→/3+(b→+c→)/3
= (a→+b→+c→)/3 となります。

つまり、
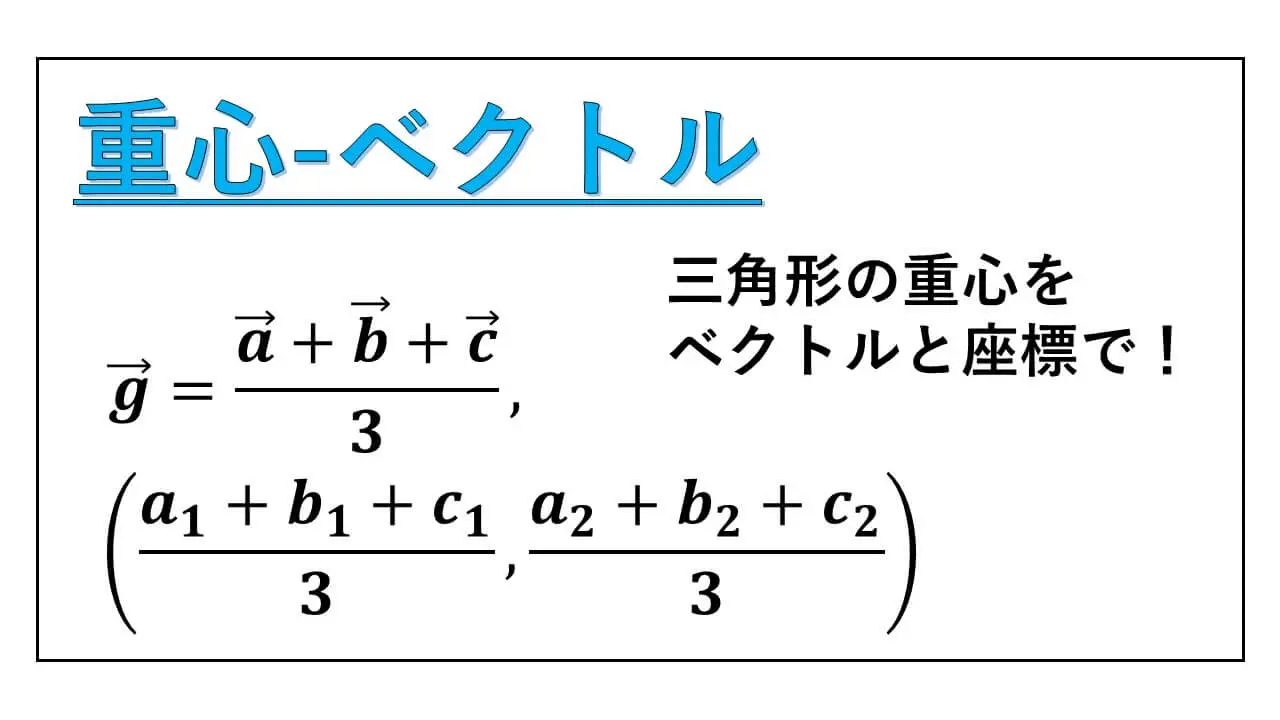
g→ = (a→+b→+c→)/3 と、重心 G を位置ベクトルで表示することができました。

三つの頂点を表す位置ベクトル全てで加法を計算し、1/3 でスカラー倍すると重心の位置ベクトルという公式になります。

この覚えやすい公式について、注意点です。

点Oが頂点の場合

先ほど、位置ベクトルの基準 O を三角形の三つの頂点と異なるとして議論を進めました。

この O が、三角形の頂点のどれかと一致していたとしても、上で述べた議論が通用します。

ただし、そのときは、点 O と一致している点の位置ベクトルが零ベクトルとなって消えます。

例えば、点 A と点 O が一致していると、
a→ = 0→ となります。

そのため、
g→ = (a→+b→+c→)/3
= (0→+b→+c→)/3
= (b→+c→)/3 となります。

本質的には同じ議論で導いている重心の位置ベクトル表示ですが、零ベクトルが絡んだために、見た目が少し変わりました。

点 B が点 O と一致しているときも、同様の式の買い替えになります。

g→ = (a→+c→)/3 となります。

点 C が点 O と一致しているときは、
g→ = (a→+b→)/3 です。

では、重心の位置ベクトル表示と、数IIで学習する座標の内容を合わせます。

重心 – ベクトル :座標

g→ = (a→+b→+c→)/3 という公式から、重心を表す座標についての公式が導かれます。

重心の位置ベクトル表示ですが、上で導いた議論は、平面ベクトルと空間ベクトルのどちらについても全く同じ議論となります。

そのため、平面座標でも空間座標でも、重心の位置を座標で表すことができます。

まず、平面座標について、重心を表す座標について述べます。

A(a₁, a₂), B(b₁, b₂), C(c₁, c₂) と三角形の頂点の座標が与えられたとします。

原点 O(0, 0) を位置ベクトルの基準とすると、それぞれの位置ベクトルを成分表示することができます。

a→ = (a₁, a₂),
b→ = (b₁, b₂),
c→ = (c₁, c₂) となっています。

g→ = (a→+b→+c→)/3 に当てはめて x 成分と y 成分の値を求めると、それぞれが x 座標の値、y 座標の値となります。

そのため、
(a₁+b₁+c₁)/3 が重心 G の x 座標の値となります。

G の y 座標の値は、
(a₂+b₂+c₂)/3 です。

ちなみに、点 A, B, C のいずれかが O と一致しているときは、先ほどと同じく消える部分が出てきます。

たとえば、
点 A と原点 O が一致しているとき、
a₁ = a₂ = 0 なので、
G の x 座標は、
(a₁+b₁+c₁)/3 = (b₁+c₁)/3 となります。

G の y 座標は、
(a₂+b₂+c₂)/3 = (b₂+c₂)/3 となります。

では、空間ベクトルについても同様の考察で座標を求めます。

空間座標について

空間座標については、z 成分が１つ増えるだけです。

g→ = (a→+b→+c→)/3 を使って、重心 G の座標が同様に得られます。

A(a₁, a₂, a₃),
B(b₁, b₂, b₃),
C(c₁, c₂, c₃) として、G の座標を求めます。

x 座標と y 座標の値は、先ほどと同じです。

z 座標の分も求めます。

(a₃+b₃+c₃)/3 が、重心 G の z 座標の値となります。

このように、平面のときと同様に異なる三点の座標から、それら三点から成る三角形の重心の座標が得られます。

関連する記事として、空間ベクトルという記事を投稿しています。

図形とベクトルを関連させる内容の記事として、内心-外心という記事で三角形の内接円の中心を位置ベクトルで表示するということを解説しています。

さらに、垂心についても位置ベクトル表示について解説をしています。

また、傍心という記事で、重心のように三角形の五心の一つである傍心に関する位置ベクトル表示について説明をしています。

また、三角比の発展内容として、
ヘロンの公式という記事で三角比とベクトルを合わせて解説をしています。

図形的な内容と、座標や三角比を合わせた考察は大学受験で頻出なので、日頃からトレーニングをしておくと良いかと思います。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。