点と直線の距離の公式 | 証明をベクトルを用いて

2024年3月25日

" 点と直線の距離の公式 “は、高校の数学IIで学習します。

この記事では、ベクトルを用いて、その証明について解説をしています。

この公式を使って問題を解く数学IIの問題もありますが、証明をベクトルを用いて行うことで、ベクトルの良い練習にもなるかと思います。

点と直線の距離とは、中学の一年の頃に学習したように、点から直線に引いた垂線の長さのことです。

この図形の内容をベクトルと絡めて式で考えることで、点と直線の公式が得られます。

点と直線の距離の公式 – 証明

【公式】

定点 A(x₁, y₁) と、
直線 l : ax+by+c = 0 が与えれたとする。

ただし、点 A は直線 l 上の点ではないとする。

このとき、点 A から直線 l に引いた垂線の足を H とすると、線分 AH の長さは次となる。

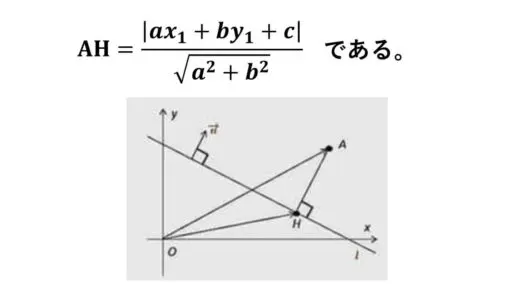
「二つのベクトルが垂直だと内積の値が 0 」ということを利用して証明を進めます。

位置ベクトルを使って、定量的に図形情報を数式化する良い練習になるかと思います。

証明開始

与えられた定数 a, b を用いて、
図のように n→ = (a, b) とします。

このベクトルは、直線 l の方向ベクトルと垂直になっています。

また、
n→ と AH→ のなす角を θ と置くと、
θ = 0° または 180° です。

よって、
n→・AH→
= |n→||AH→|cos θ
= ±|n→||AH→| となります。

内積の値は実数値なので、絶対値をつけると 0 以上の実数ということになります。

それゆえに、絶対値をつけると、
次のように ± の部分を 0 以上として扱うことができます。

つまり、
|n→・AH→| = |n→||AH→| です。

点 A は直線 l 上の点ではないため、
|AH→| ≠ 0 です。

よって、
|AH→| = |n→・AH→| ÷ |n→|
= |n→・AH→|/|n→| …①

垂線の足の座標を文字で置く

垂線の足である点 H の座標を
(p, q) と置きます。

原点 O(0, 0) を位置ベクトルの基準として平面ベクトルを成分表示しています。

そのため、OH→ = (p, q) です。

内積を計算すると、
n→・OH→ = ap+bq です。

また、
点 H(p, q) は直線 l 上の点より、
ap+bq+c = 0 なので、
ap+bq = －c です。

よって、
n→・OH→ = －c となります。

自分で文字を置いたことで、内積の値を －c で書き換えることができました。

これが、後半の証明の決め手になります。

証明の後半

A の座標が (x₁, y₁) だったので、
OA→ = (x₁, y₁) です。

n→・AH→ = n→・(OH→－OA→)
= n・OH→－n・OA→
= －c－(ax₁+by₁)
= －(ax₁+by₁+c)

両辺に絶対値をつけると、
|n→・AH→| = |ax₁+by₁+c| …②

①より、
|AH→| = |n→・AH→|/|n→| でした。

|n→| = (a²+b²)^1/2 より、
②から、
AH = |AH→|
= |ax₁+by₁+c|÷(a²+b²)^1/2 です。【証明完了】

はじめから、AH の長さを求めたかったわけですが、H の座標を自分で設定し、直線 l の法線ベクトルを使うところが、ベクトルの良い練習となる証明かと思います。

理系でベクトルを使うときには、直線の方向ベクトルと法線ベクトルと直線を表す方程式を結びつけておくことが大切になります。

次に、導いた点と直線の距離の公式を使ってみます。

点と直線の距離の公式 :使う練習

【練習問題１】

y = x² 上の点 A を (2, 4) とします。

また、直線 l の方程式を、
－3x+4y = 1 とします。

このとき、点 A と直線 l との距離を求めてください。

点と直線の距離の公式を使うときに、直線を表す式を右辺が 0 とした形に移項してから公式を使います。

そのため、
－3x+4y－1 = 0 として先ほどの公式を使うことになります。

つまり、
a = －3, b = 4, c = －1 ということです。

先ほどの x₁ として 2、y₁ として 4 を使います。

これで、点 A と直線 l との距離を表す式を計算することができます。

公式の分子の値は、
|ax₁+by₁+c| でした。

これに該当する値を代入します。

すなわち、
|－3・2+4・4－1|
= |－6+16－1|
= |9| = 9 です。

これで、求めたい距離の値の分子にくるのが 9 と分かりました。

分母の値も計算

分母の値は、a²+b² にルートをつけたものになります。

今、a = －3, b = 4 より、
{(－3)²+4²}^1/2
= 25^1/2 = (5²)^1/2

ここで、5 > 0 より、
{(－3)²+4²}^1/2 = 5 となります。

これで、公式の分母の値が 5 と分かりました。

分子の値 9 を分母の値 5 で割ると求めたい距離となります。

すなわち、9/5 が求める点と直線の距離です。

公式は一気に表示した式ですが、分子の値と分母の値を分けて、それぞれ求めておいてから割り算をするというように計算の工程を分けることができます。

分数は「分子の値を分母の値で割った値」ということは、意外と様々なところで使えます。

また、数学IIでは、指数が有理数というときもでてきます。

※ 分数指数という少し複雑な指数の記事も投稿しています。

そのために、普段の学習から意識をしておくと自然と練習になるかと思います。

今度は、文字（パラメータ）を使った練習を扱ってみます。

長さが最も短くなるときの値

【練習問題２】

y = x² 上の点 A を (p, p²) とします。

また、直線 l の方程式を、
－3x+4y = －1 とします。

点 A と直線 l との距離が最小になるときの p の値を求めてください。

－3x+4y+1 = 0 という形にしておいてから、点と直線の距離の公式を使います。

点 A(p, p²) から直線 l に引いた垂線の足を H とします。

点と直線の距離の公式で表される長さは、AH の長さということになります。

公式の分母にくる値は、
{(－3)²+4²}^1/2 = 5 で、先ほどの練習問題と同じ値の定数になっています。

分子にくる値は、
|－3p+4p²+1| です。

よって、
AH = |4p²－3p+1|/5 …★

パラメータ p が実数を動くために、AH の長さが変化します。

ここで、AH の長さが最小となるときの p の値を求めるというのが、この【練習問題２】の本質的な内容になります。

★の AH を表す式の分母は 5 という定数なので、変化する分子の値に注目します。

そこで、f(p) = 4p²－3p+1 と置きます。

平方完成をすると、
f(p) = 4(p－3/8)²－4・(3/8)2+1
= 4(p－3/8)²－9/16+1
= 4(p－3/8)²+7/16 です。

ここで、f(p) は下に凸の二次関数です。

ゆえに、
f(p) が取り得る値は、
7/16 以上ということになります。

この内容と★の式を合わせてみます。

AH = |f(p)|/5
= |4(p－3/8)²+7/16|/5
≧ |7/16|/5 = 7/80

これで、AH の最小値が 7/80 ということが分かりました。

ただし、問題の質問内容は、AH が最小となるときの p の値についてです。

AH の値が最小となるときというのは、f(p) の値が最小となるときです。

つまり、f(p) の値が最小となるときの p の値が求める値です。

二次関数の式を標準形にしたときのことを思い出します。

f(p) = = 4(p－3/8)²+7/16 だったので、
頂点の x 座標の値である
p = 3/8 が求める値です。

標準形にするときの計算でミスがあると、求める答えが連動してまちがってしまうので、分数や符号に注意した正確な計算は大切になります。

あらゆる単元で二次関数を標準形にして最大や最小を求めることが多いので、この計算には慣れておくと良いかと思います。

また、点と直線の距離の公式は、三角形の高さを求めることにも役立ちます。

ただ、この高さと三角形の面積ですが、三角比で学習した内容とベクトルとの合わせ技で面積を求める公式があります。

ベクトルに関連して、それについて述べておきます。

図形と計量で高さに関して

【三角形の面積公式】

三角形OAB について、
a→ = OA→, b→ = OB→ とし、
∠AOB = θ とする。

また、三角形OAB の面積を S とする。

このとき、
S = 1/2×(|a→|²|b→|²－|a→|²|b→|²cos²θ)^1/2
= 1/2×(|a→|²|b→|²－(a→・b→)²)^1/2 である。

＜証明＞

三角比の単元で学習したように、
S = 1/2×OA×OB×sin θ です。

なす角 θ は 0° から 180° の範囲で、
sin θ の値は 0 より大きくなっているという状況です。

そのため、
sin θ = (1－cos²θ)^1/2 と表すことができます。

さらに、
OA = |a→|, OB = |b→| と線分の長さをベクトルの大きさを使って表しておくと、次のように式を書き換えることができます。

S = 1/2×OA×OB×sin θ
= 1/2×|a→||b→|(1－cos²θ)^1/2
= 1/2×(|a→|²|b→|²－|a→|²|b→|²cos²θ)^1/2

さらに、ベクトルの内積を使って式を書き換えます。

a→・b→ = |a→||b→|cos θ より、
|a→|²|b→|²cos²θ
= (|a→||b→|cos θ)²
= (a→・b→)² です。

そのため、
S = 1/2×(|a→|²|b→|²－|a→|²|b→|²cos²θ)^1/2
= 1/2×(|a→|²|b→|²－(a→・b→)²)^1/2 となっています。

これで結論の二つの等式が得られました。【証明完了】

|a→| = OA > 0 なので、
|a→| = (|a→|²)^1/2 より、二乗して絶対値の中に入れることができます。

これが式の書き換えの決め手となりました。

今度は、座標平面上で点 A と点 B の座標が得られているという状況で、示した面積の公式をベクトルの成分表示を利用して書き換えます。

以下では、点 O(0, 0) を原点として議論を進めています。

成分表示を利用した面積

【面積の公式２】

A(a₁, a₂), B(b₁, b₂) について、
三角形OAB の面積を S とする。

このとき、
S = 1/2 × |a₁b₂－a₂b₁| である。

＜証明＞

a→ = OA→ = (a₁, a₂),
b→ = OB→ = (b₁, b₂) がベクトルを成分表示で表したものです。

先ほど示した面積の公式を、この成分表示をもとにして成分の計算をすると、求めたい等式が得られます。

1/2×(|a→|²|b→|²－(a→・b→)²)^1/2 が面積 S の値なので、ベクトルの大きさと内積の値を成分を使って計算するというわけです。

|a→|² = a₁²+a₂²,
|b→|² = b₁²+b₂² です。

そして、内積の値は、
(a→・b→)² = (a₁b₁+a₂b₂)² です。

そのため、
|a→|²|b→|²－(a→・b→)²
= (a₁²+a₂²)(b₁²+b₂²)－(a₁b₁+a₂b₂)²
= a₁²b₂²+a₂²b₁²－2a₁a₂b₁b₂
= (a₁b₂－a₂b₁)² となります。

よって、
S = 1/2×(|a→|²|b→|²－(a→・b→)²)^1/2
= 1/2×{(a₁b₂－a₂b₁)²}^1/2
= 1/2×|a₁b₂－a₂b₁| 【証明完了】

a₁b₂－a₂b₁ の値は、負の実数となるときもあるので、最後のルートをとるときに、絶対値をつけます。

三角形の高さを求めるときに必要な点と直線の距離の公式と、三角比を用いた三角形の高さに関してベクトルを使ってアプローチしました。

ベクトルは様々な分野で使われるので、慣れておくと役立ちます。

【関連する記事たち】

この記事で、垂直ということとベクトルの内積からアプローチをしました。

内積の定義という記事で、なす角を用いた内積の定義と、成分表示を用いた内積の定義について解説をしています。

直線の傾きと垂直については、
二直線が垂直という記事で、数IIで学習する垂直に交わる直線の傾きの積が －1 になるということの証明を三角形の相似を用いて解説しています。

平面図形の内容とベクトルを合わせた受験問題は多いです。

チェバの定理の逆という記事で、そのような受験の頻出内容を解説しています。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。