アポロニウスの円 | 軌跡について数2から複素数平面の考え方へ
" アポロニウスの円 “は、二つの定点からの距離の比が一定である点全体となっています。
数学2の軌跡の単元でも出てきます。また、複素数平面の単元でも扱われます。
まずは、xy-座標平面において、数学2で学習する内容で、具体的なアポロニウスの円を表す軌跡の方程式を求めます。
その後で、複素数平面の考え方で、アポロニウスの円を扱います。
なお、この記事では、虚数単位を i と表しています。
i2 は -1 となります。
アポロニウスの円 :数2の考え方で軌跡
アポロニウスの円は、二つの定点からの距離の比が一定である点全体となっています。
ただし、距離の比は、1:1 ではないものとします。
点 A, B という座標平面上の異なる点について、二点 A, B からの距離の比が 1:1 である点全体は、線分ABの垂直二等分線となることを中学一年生の数学で学習しています。
垂直二等分線は直線なので、円ではありません。
そのため、アポロニウスの円を考えるときは、二つの定点からの距離の比が 1:1 ではないという仮定の下で議論をします。
ちなみに、二直線が垂直ということは、数学2では、直線の傾きの積が -1、ベクトルでは方向ベクトルどおしの内積が 0 ということです。
この内容も、図形と方程式について基本となるので大切です。
それでは、具体的な内容を使って、アポロニウスの円を求めてみます。
軌跡を表す方程式を求める
【問題1】
点 (-3, 0), (0, 0) からの距離の比が、
2:1 である点全体が表す図形の方程式を求めてください。
求める図形上の点を (x, y) とします。
x と y を用いた等式を作ることを考えます。
点 (-3, 0) と (x, y) の二点間距離は、
三平方の定理より、
{(x+3)2+y2}1/2 です。
点 (0, 0) と (x, y) の距離は、同様に、
(x2+y2)1/2 です。
距離の比が 2:1 ということから、
{(x+3)2+y2}1/2 : (x2+y2)1/2 = 2 : 1 となっています。
外項の積と内項の積が等しくなることから、
{(x+3)2+y2}1/2 = 2(x2+y2)1/2
両辺を二乗すると、
(x+3)2+y2 = 4(x2+y2) です。
ちなみに、
(x+3)2+y2 = 4(x2+y2) が成立すれば、
{(x+3)2+y2}1/2 = 2(x2+y2)1/2 と逆の式の書き換えができます。
そのため、外項の積と内項の積が等しいことから、
距離の比が 2:1 であることまでへも、さかのぼることができます。
では、(x+3)2+y2 = 4(x2+y2) を同値変形します。
x2+6x+9+y2 = 4x2+4y2 より
3x2-6x-9+3y2 = 0
そのため、
x2-2x-3+y2 = 0
(x-1)2-1-3+y2 = 0 より、
(x-1)2+y2 = 22 です。
同値変形をしたので、
(x-1)2+y2 = 22 が成立すると、
(x+3)2+y2 = 4(x2+y2) も成立することになります。
よって、
「点 (x, y) と (-3, 0), (0, 0) の距離の比が 2:1 である」ことと、
「(x-1)2+y2 = 22 が成立する」ことは、同値です。
(x-1)2+y2 = 22 は、
中心 (1, 0)、半径 2 の円です。
以上より、これが求める軌跡を表す方程式です。
この内容で、円の方程式を求めた後に、「逆も明らか」と述べられることが多いです。
必要条件を求めてから十分条件でもあることを確認する流れについて、十分性が明らかということです。
今の議論では、常に逆が成立することを確かめながら同値であることを述べてきたので、「逆は明らか」という記述をしていません。
軌跡を考えるときは、論理が背後にあるので、同値な書き換えになっているのかどうかを常に押さえておくことが大切になります。
ちなみに、軌跡については、二次関数の平行移動で、高校一年の段階から触れていますので、平行移動を通じて、平行移動後の軌跡を表す方程式を求める練習をするのも良い復習になるかと思います。
これについては、放物線の軸という記事で解説をしています。
ここまでが、数学2の軌跡の単元の内容です。
それでは、数Cの複素数平面の内容で、アポロニウスの円を議論します。
アポロニウスの円 :準備に数と点の対応
中学一年の数学で、実数の 3 と数直線上の点 3 を対応させました。
数と図形内の点を対応させるということについて、
3+2i という複素数に、
座標平面内の点 (3, 2) を対応させます。
z = a+bi (a, b は実数) に対して、
座標平面内の点 (a, b) が対応です。
複素数に対して、点を対応させているときに、
xy-座標平面のことを複素数平面といいます。
複素数平面を考えることによって、図形的なアプローチができるときもあるので、問題を解くための方法が豊かになります。
複素数平面は、xy-座標平面ですが、横軸である x 軸のことを実軸、縦軸である y 軸のことを虚軸といいます。
3i = 0+3i という純虚数に対応する点は、
点 (0, 3) という縦軸上の点です。
対称移動など図形的な内容
z = a+bi (a, b は実数) について、
z = a-bi を z の共役複素数といいます。
図形的には、z に対応する点 (a, b) を、
横軸である実軸について対称に折り返したものが、
点 (a, -b) です。
この点 (a, -b) に対応する複素数が、
z という共役複素数です。
また、図形とは別に、複素数についての計算で、
zz = a2+b2 と分かります。
また、|z| = (a2+b2)1/2 なので、
zz = = |z|2 です。
また、二つの複素数 α と β に対応する点を、
それぞれ (p, q), (s, t) とします。
|α-β| = {(p-s)2+(q-t)2}1/2
これは、(p, q) と (s, t) について、
xy-座標平面で三平方の定理を使って定義した二点間の距離と同じ値になっています。
そのため、|α-β| は、α と β に対応する点についての二点間距離となっています。
このように、計算結果と図形的な内容を合わせて考えることが多い複素数平面です。
点 A(p, q), B(s, t) に対応する複素数を α, β とし、
A, B からの距離が 1:1 である点を C とし、
C に対応する複素数を z とします。
すると、点 C は、線分ABの垂直二等分線上の点で、点 C と A の距離は、点 C と B の距離に等しいことになります。
これを複素数の絶対値を用いて表すと、
|z-α| = |z-β| ということになります。
この方程式を満たす複素数 z に対応する点は、α, β に対応する点から等しい距離にあるということを表しています。
この、二定点からの距離の比が、
1:1 ではないという設定の下で、アポロニウスの円を考えます。
それでは、アポロニウスの円を複素数平面の考え方で求める練習問題です。
アポロニウスの円 :複素数で考えると
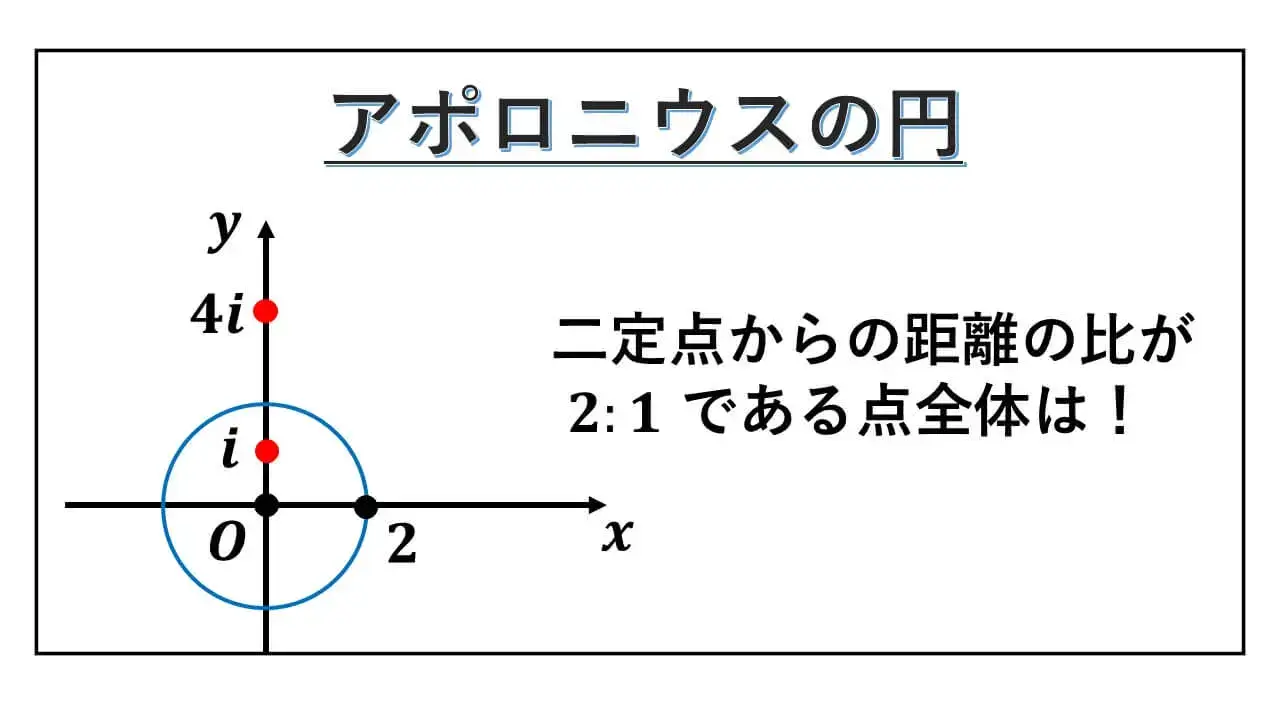
二点 A(0, 4), B(0, 1) に対応する複素数は、
それぞれ、4i と i です。
この A, B からの距離の比が 2:1 である点全体が表す図形を求めます。
複素数 z に対応する点 C と、A, B とのそのぞれの距離の比が、2:1 だとします。
この内容を複素数の絶対値で距離を表すと、
|z-4i| : |z-i| = 2 : 1 です。
外項の積と内項の積が等しいので、
|z-4i| = 2|z-i| です。
両辺を二乗すると、
|z-4i|2 = 4|z-i|2 となります。
二乗を共役複素数を用いて表す
|z-4i|2 は、z-4i と、その共役複素数の積です。
z-4i の共役複素数は、z+4i です。
そのため、
|z-4i|2 = (z-4i)(z+4i) となります。
同様に、
|z-i|2 = (z-i)(z+i) です。
これらの内容を踏まえると、次のようになります。
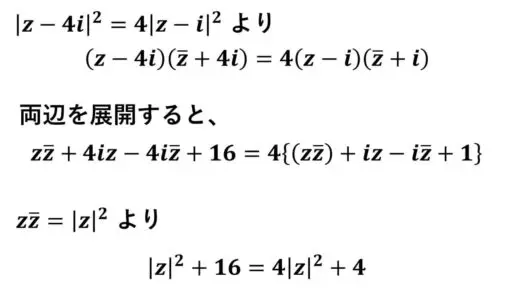
移項すると、-3|z|2 = -12 となり、
|z|2 = 4 です。
|z| ≧ 0 より、
|z| = 2 となります。
すなわち、|z-0| = 2 です。
これは、z に対応する複素数 C と、
0 に対応する (0, 0) の距離が 2 ということを示しています。
そのため、点 C は、
原点 (0, 0) を中心とする半径 2 の円周上の点ということになります。
これで、求める図形が分かりました。
この内容も、逆については、同値なので成立しています。
よって、二定点 A, B からの距離の比が 2:1 である点全体が表す図形は、原点中心の半径 2 の円と決定できました。
このように、複素数の計算と、複素数平面における図形的な情報を、どちらも考えながら議論を進めるのが、この単元で重要なことになります。
z と z の共役複素数で積をとると、絶対値の二乗となることは、しばしば使われるので、押さえておくと良いかと思います。
また、z = a+bi (a, b は実数)という複素数について、
|z| は実数となります。
実数については、通常の大小関係が利用できるので、大小関係を考えると可能性を絞り込めるときもあります。
先ほどは、|z|2 = 4 という場面で、
|z| が 0 以上の実数ということから、
|z| = 2 と決定しました。
|z| の値が負の実数にはならないということも、しばしば利用できます。
関連する記事として、ド・モアブルの定理という複素数平面についての記事を投稿しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。