個数定理 | 3つの集合の和集合に含まれる要素の個数を求める公式を証明【2つのときから論理的に学習】
三つの有限集合の和集合についての「 個数定理 」を証明します。二つの有限集合の和集合についての個数定理から始めて、論理的に三つの集合へと発展させます。
ベン図から直観的に解釈することもできますが、数式を用いて論理的に導くことは大切になります。
問題文を読んだときに、感覚的に判断が難しいときこそ、論理を用いて正確に考えることが必要かと思います。
この個数定理を理解するためには、高校の集合単元で扱われる記号の使い方と、論理についての基礎的な運用が重要です。
この記事では、有限集合 A に含まれている要素の個数を、n(A) と表すことにします。
A と B を有限集合としたとき、
A∪B や A∩B も一つの有限集合なので、含まれている要素の個数は、
それぞれ n(A∪B), n(A∩B) となります。
まず、二つの有限集合の和集合についての個数定理から解説します。
その後で、三つの有限集合の和集合についての個数定理へと話を発展させます。
個数定理 :使う記号について
全体集合 U の部分集合を A とするときに、U における A の補集合を Ac と表すことにします。
A, B ⊂ U に対して、
(A∪B)c = Ac∩Bc,
(A∩B)c = Ac∪Bc というド・モルガンが成立します。
よく使う記号ですが、有限集合 A, B ⊂ U について、A∩Bc は、A の要素で B に含まれていないものを全て集めたものです。
定義から、「A の要素であり、かつ、B に含まれていない U の要素」ということです。
そのため、「A の要素だけれども、B に含まれていない要素」ということになります。
※ 要素(元)という記事で、集合の要素や部分集合についての基礎的な内容を解説しています。
この定義から、n(A∩Bc) を求めると、
n(A) - n(A∩B) となります。
A の要素だけれども、B に含まれていない要素は、A の要素から、A∩B の要素を取り除いたものだからです。
よって、
n(A∩Bc) = n(A) - n(B) となります。
2つのときの個数定理
有限集合 A, B ⊂ U について、和集合 A∪B の要素は、次の三つのタイプのどれかに必ずなります。
「A の要素だけれども B の要素でないもの」、
「A の要素であり B の要素でもあるもの」、
「A の要素ではない B の要素」という三つのタイプです。
A∪B のどの要素も、論理的に、これらの二つの部分集合に重複して含まれていません。
補集合の記号を用いて表すと、
A ∪ B =
(A∩Bc)∪(A∩B)∪(Ac∩B) ということになります。
含まれている要素の個数について、
n(A ∪ B)=
n(A∩Bc)+n(A∩B)+n(Ac∩B) となっています。
先ほど述べたことから、
n(A∩Bc) = n(A) - n(A∩B) です。
同様に、
n(Ac∩B) = n(B) - n(A∩B) となります。
よって、
n(A∩Bc)+n(A∩B)+n(Ac∩B) =
{n(A) - n(A∩B)}+n(A∩B)
+{n(B) - n(A∩B)}
= n(A) + n(B) - n(A∩B) となります。
※ 共通部分と和集合については、リンク先の記事で基礎となる内容を解説しています。
まとめると、次の個数定理となります。
【個数定理】
n(A ∪ B)=n(A) + n(B) - n(A∩B)
この二つの有限集合についての個数定理を、三つの有限集合の和集合のときに、どうなるのかを考えます。
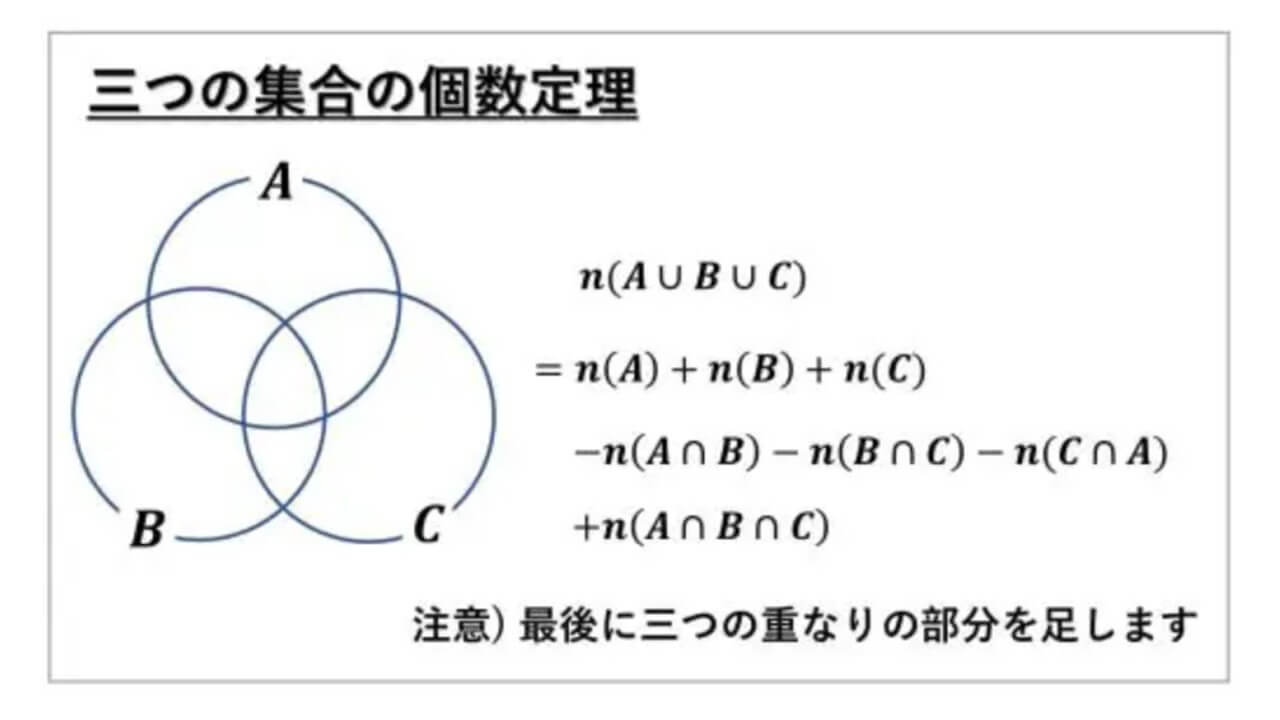
個数定理 :3つの有限集合のとき
【3つの集合で個数定理】
U を全体集合とし、
A, B, C ⊂ U を有限集合とする。
このとき、n(A∪B∪C) は、
n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)
-n(C∩A)+n(A∩B∩C) に等しい。
三つの集合についての個数定理では、重なっている共通部分が重複して数えてしまっているので、それぞれ引きます。
しかし、中央の三つの重なりの部分の個数が、一回分だけ多く引き過ぎているので、最後に n(A ∩ B ∩ C) を加えるというのが覚え方です。
この内容は、感覚的に理解しにくいかと思いますので、客観的に数式を用いて示しておきます。数式の根拠となるのが、次の図の内容です。
ただ、毎回、導くのも大変なので、覚え方として、
-n(A∩B)-n(B∩C)-n(C∩A) という輪環の順の部分を引いてから、
最後に中央の n(A∩B∩C) を足すと記憶しておくと良いかと思います。
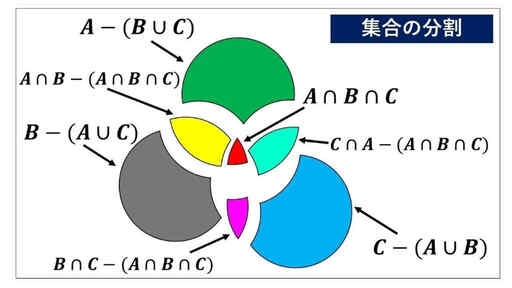
A -(B ∩ C) などは、差集合といって、左の集合から右の集合の要素を除いた残りだけを集めた集合です。
※ 補集合という記事で、差集合について解説をしています。
この A∪B∪C の分割を根拠に、個数定理を証明します。
3つの個数定理の証明
n(A-n(B∪C) = a(濃い緑)
n(A∩B-A∩B∩C) = b(黄)
n(A∩B∩C) = c(赤)
n(C∩A-A∩B∩C) = d(薄い緑)
n(B-A∪C) = e(灰色)
n(B∩C-A∩B∩C) = f(紫)
n(C-A∪B) = g (青)と置きます。
上の図に描いている七個の集合に含まれている要素の個数をすべて合わせると、A ∪ B ∪ C に含まれている要素の個数の合計となります。
n(A ∪ B ∪ C) は、これら全ての和です。
よって、次の等式を得ます。
n(A ∪ B ∪ C) =
a+b+c+d+e+f+g =
(a+b+c+d)+(b+c+e+f)
+ (c+d+f+g) - (b+c)
- (c+f) - (c+d) + c
真ん中の辺と最後の長い辺で、文字式の計算をすると一致しています。
実際に文字式の計算をすると、
(a+b+c+d)+(b+c+e+f)+(c+d+f+g)
-(b+c)-(c+f)-(c+d)+c
= a+2b+3c+2d+e+2f+g
-(b+c)-(c+f)-(c+d)+c
= a+2b+3c+2d+e+2f
-(b+3c+d+f)+c
= a + b +d + e + f + c
= a + b + c + d + f + e
となっています。
よって、
n(A ∪ B ∪ C) =
(a+b+c+d)+(b+c+e+f)
+ (c+d+f+g)-(b+c)
- (c+f)-(c+d)+c
右辺が表す要素の個数は、図より、
n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)-n(C∩A)+n(A∩B∩C) となっています。
これで、三つの集合についての個数定理の証明ができました。
黄と赤 = b + c = n(A∩B),
赤と紫 = c + f = n(B∩C),
赤と薄い緑 = c + d = n(C∩A) となっています。
個数定理は、集合単元の問題としても出題されますし、数学全般で、論理の考え方が基礎になるので、個数定理は良い学習になるかと思います。
場合の数の単元の内容と合わせた考察も大切になるので、取り挙げておきます。
個数定理 :場合を考える
【問題1】
300 以下の自然数全体の中に、「3の倍数または5の倍数」が何個あるのかを考えます。
ここで、集合という事象を設定します。
1 以上 300 以下の自然数全体を全体集合を U と置きます。この U が全体集合(全事象)です。
この U の要素で、3の倍数となっているものをすべて集めて A とします。
{x∈U | x は3の倍数} が A です。
この A に含まれる要素の個数を n(A) と表します。この n(A) の値が、300 以下の3の倍数の個数を表します。
また、{y∈U | y は5の倍数} を B と置きます。
n(B) が、300 以下の5の倍数の個数です。
300 以下の自然数全体の中に、「3の倍数または5の倍数」が何個あるのかを、n(A) や n(B) を使って求めます。
300 以下の自然数全体の中に含まれる「3の倍数または5の倍数」をすべて集めた集合(事象)は、A と B の和集合(和事象)となります。
A ∪ B に含まれている要素の個数が、求める場合の数の総数となります。
和集合に含まれている要素の個数についての考察なので、個数定理を使うチャンスです。
n(A ∪ B) =
n(A)+n(B)-n(A ∩ B) …★となっています。
A ∩ B という共通部分(積事象)が、300 以下の自然数で、3の倍数であり、かつ5の倍数である整数です。
この部分が重複しているので、n(A ∩ B) を引くことになります。
★の公式より、
n(A), n(B), n(A ∩ B) たちを求めます。
300 以下の自然数の中で、3の倍数をすべて集めたものが A でした。
3×1, 3×2, … , 3×100 が、A に含まれる要素のすべてです。
よって、n(A) = 100 です。
300 以下なので、3×100 も含まれるので、注意です。
n ≦ 300 の定義は、
n = 300 または n < 300 を満たすということです。
同じ様に、n(B) も求めます。
5×1, 5×2, … , 5×60 の 60 個が、B に含まれる要素の総数です。
よって、n(B) = 60 です。
倍数と「かつ」
3の倍数、かつ5の倍数というと、3の倍数であり、なおかつ5の倍数ということです。
そのため、A ∩ B の要素は、3 と 5 の公倍数で 300 以下の自然数です。
公倍数は、最小公倍数の倍数となっています。
そのため、15 の倍数で、300 以下の自然数であるものをすべて集めたものが何個あるのかを考えます。
15×1, 15×2, … , 15×20 の 20 個が、300 以下の 15 の倍数です。
よって、n(A ∩ B) = 20 となります。
以上より、★から、
n(A ∪ B) =
n(A)+n(B)-n(A ∩ B)
= 100+60-20
= 140 となります。
これで、300 以下の自然数で、3の倍数であり、かつ5の倍数である整数が 140 個だと分かりました。
次の問題は、順列と組合せを意識する内容の整数を扱う問題です。
順列だけではない考察
【問題2】
2, 3, 4, 5 という異なる 4 つの整数から、異なる 3 つの数字を取って 3 桁の整数を作ります。このとき、その 3 桁の整数で、3 の倍数となっているものは何個あるのかを求めます。
この問題を解くときに、順列と組合せの違いを理解しておくことが重要になります。
例えば、2, 4, 5 と異なる 3 個を取ったときに、2, 4, 5 を並び替えたものをすべて 1 通りと見なすのが組合せです。
そのため、2,4,5 や 5,2,4 や 4,5,2 は、どれも組合せとしては、2 と 4 と 5 を選んだ 1 通りということになります。
それに対して、並び替えたものは異なるものと考えるのが順列です。
2,3,4 、2,4,3 、3,2,4 、
3,4,3 、4,2,3 、4,3,2 という樹形図の発想で並び替えた 3! 通りが順列です。
2, 3, 4, 5 という異なる 4 つの整数から、異なる 3 つの数字を取って 3 桁の整数を作るという過程を、次の二つの過程に分解して、それぞれ何通りかを考えます。
【過程①】
異なる 4 個から異なる 3 個を選ぶ組合せ
【過程②】
選んだ異なる 3 個を並び替える順列
まず、過程①から考えます。
異なる 4 個から異なる 3 個を選ぶ組合せの総数は、
4C3 = 4 通りです。
具体的には、
2,3,4 、2,3,5 、
2,4,5 、3,4,5 という 4 通りの組合せが考えられます。
今、具体的に書き出しましたが、辞書式配列法で考えて書き出しました。
まず【過程①】で、4 通りの組合せができます。
選ばれた 4 個の組合せのそれぞれを、並び替えるのが【過程②】です。
「2,3,4」という組合せだと、この異なる 2, 3, 4 を並び替えて 6 通りの順列ができます。
1 つの組合せから、6 個の順列ができるので、
4 × 6 = 24 通りの 3 桁の整数ができることになります。
ただし、求める場合の数は、3 の倍数という条件がついています。
そこで、3の倍数判定法を使って、【過程①】の段階で、条件に合わないものを除外します。
倍数判定法から、各位の和が 3 の倍数となっている組合せだけを残します。
条件を満たさないものを除外
2,3,4 の組合せについては、
2+3+4 = 9 より、3の倍数判定法から、各位の和が3の倍数であることから、条件を満たします。
加法の結合法則と交換法則から、2, 3, 4 を並び替えをした 6 個の 3 桁の整数は、どれも3の倍数です。
組合せ 2,3,5 については、
2+3+5 = 10 より、3の倍数ではないことが分かります。
そのため、2,3,5 の組合せは、【過程②】の前の段階で除外します。
組合せ 2,4,5 についても、
2+4+5 = 11 より、3の倍数ではないため、除外します。
組合せ 3,4,5 は、
3+4+5 = 12 より、3の倍数となることが分かります。
以上より、組合せ 2,3,4 の 3 つの整数を並べ替えてできる整数 6 個と、組合せ 3,4,5 の並び替えによる 6 個の整数が、求める3の倍数です。
これで、求める3の倍数の個数が、
6+6 = 12 だと分かりました。
ここでも、「または」という論理を用いました。
組合せが 2,3,4 のとき、または、組合せが 3,4,5 のときが、選んだ 3 個の整数を並び替えると、求める3の倍数となるときということでした。
この【問題2】では、3の倍数ということだったので、3の倍数判定法を使いましたが、5の倍数ということにして、新しい問題を考えてみます。
状況が変わると、数え方を柔軟に対応させることも大切になるかと思います。
互いに排反であることについて
【問題3】
0, 1, 2, 3 の 4 つの整数から 3 個の整数を選び 3 桁の整数を作ります。ただし、百の位に 0 を置かないものとします。
このとき、3 桁の整数が何個できるかを考えます。
0, 1, 2, 3 の 4 つの整数から 3 個の整数を選んでできる 3 桁の整数全体を U とします。
この全体集合 U の部分集合を A, B を次のものとします。
U に含まれる 3 桁の整数で、どの位にも 0 がないものをすべて集めたものを A とします。
U に含まれる 3 桁の整数で、どこかの位に 0 があるものをすべて集めたものを B とします。
場合の数・確率の単元の用語では、U を全事象といい、A と B を U に含まれる事象といいます。
事象 A に含まれることを否定すると、事象 B に含まれることになります。
そのため、A ∩ B は空集合となっています。
共通部分が空集合となっているとき、二つの事象は、互いに排反といいます。
互いに排反であるときは、
n(A ∩ B) = 0 です。
空集合には、含まれる要素が無いため、含まれる要素の個数は 0 個ということです。
このことと、個数定理を合わせると、A と B が互いに排反であるとき、
n(A ∪ B) = n(A)+n(B) となります。
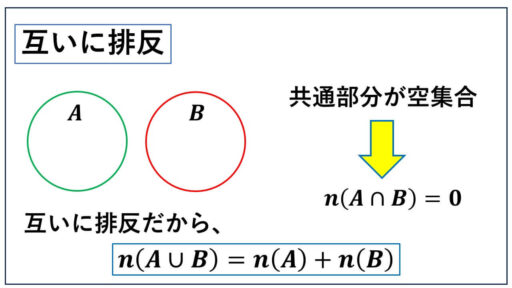
このイメージで、互いに排反と個数定理を結び付けて押さえると良いかと思います。
二分割されている状況
今、0, 1, 2, 3 の 4 つの整数から 3 個の整数を選んでできる 3 桁の整数全体を U とし、U を全事象として考えていました。
U に含まれる 3 桁の整数は、どこかの位に 0 があるか、どの位にも 0 が無いかのいずれかです。
そのため、
U = A ∪ B であり、
A ∩ B が空集合となっている状況です。
そのため、
n(U) = n(A ∪ B) = n(A)+n(B) です。
U に含まれる 3 桁の整数で、どの位にも 0 がないものをすべて集めたものが A だったので、A に含まれている要素の個数は次のようにして求めることができます。
0 が、どの位にも無いため、1, 2, 3 を並び替えてできる 3 桁の整数が A の要素です。
そのため、
n(A) = 3P3 = 6 です。
U に含まれる 3 桁の整数で、どこかの位に 0 があるものをすべて集めたものが B でした。
今度は、n(B) を求めます。
百の位には 0 を置くことができない設定なので、0 が十の位に置かれている場合と、0 が一の位に置かれている場合が考えられます。
【十の位が 0 のとき】
1, 2, 3 から異なる 2 個の整数を選び、百の位と一の位に配置することになります。
そのため、
3P2 = 3×2 = 6 通りの整数の作り方があります。
【一の位が 0 のとき】
1, 2, 3 から異なる 2 個の整数を選び、百の位と十の位に配置することになります。
同様に、3P2 = 6 通りの整数の作り方があります。
よって、n(B) = 6+6 = 12 です。
したがって、
n(U) = n(A)+n(B)
= 6+12 = 18
これで、0, 1, 2, 3 の 4 つの整数から 3 個の整数を選んでできる 3 桁の整数の個数が、18 個だと決定できました。
今回の記事では、場合の数だけを考えました。
同様に確からしいという記事で、高校数学の確率についての基礎的なことを解説しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。