円の内部 – 領域 | 数学2の単元内容でも論理と集合を考える

数学IIで、「 円の内部 」や「 円の外部 」といった" 領域 “を用いて学習します。
xy-座標平面は、二組の実数の組 (a, b) という点たちを集めた集合です。この集合の部分集合のことを領域といいます。
集合ということは、高校一年のときに学習した論理を使った命題の考え方が使えます。
大学の数学では、頻繁に集合と論理を使いますが、高校の内容で、知っている図形を通じて練習しておくと良いかと思います。
数学では、条件について、当てはまるものをすべて集めた集合を考えることが多いです。そして、論理と関連させながら、共通部分や和集合を使って議論を進めていくこともします。
条件と集合を合わせて日頃から考える習慣をつけておくと、数学の理解が深まっていくかと思います。
円の内部 – 領域 :命題に使われる変数
円の内部や外部の内容の議論の前に、数学全般に渡って使われる命題と論理についての内容を解説します。
この内容を基にして、数学の議論が展開されます。そのため、数学におけるルールとして把握をしておくことが大切になります。
条件どおしについて、「かつ」や「または」が関連してきたときに、文章を集合で表してみると、意外とすぐに解決することも多いです。
「 仮定条件 」に「 変数 」が使われているときに、その変数の範囲に注意が必要となります。
命題の仮定条件と結論条件だけでなく、使われている変数の範囲も真偽に関わってくるので、確認が必要になります。
「仮定条件 p ならば、結論条件 q が成立する」という命題に変数が使われるときに、変数を見つけてどういう範囲なのかということを押さえることを日頃から意識しておくと良いかと思います。
前提となる変数の範囲
難しい証明が必要な命題だと、命題に使われている変数が分かりにくいかと思います。そのため、真偽がすぐに分かるような命題を例にして説明していきます。
「仮定条件に使われている変数」について、特に意識をしておくと良いかと思います。
【命題の具体例】
x を実数とする。
このとき、x ≠ 0 ならば、x ≧ 2 である。
この命題では、変数として x が使われています。この変数について、議論をするときの範囲が前提として示されています。
x は実数ということなので、虚数を x に代入するということは NG となります。
命題について議論をするときに、変数が動く範囲を先に確定させておかないと、命題の真偽に関わるため、注意です。
この【具体例】としている命題は、変数 x に代入することができる値の範囲が、実数全体から成る集合の要素(元)となっています。
結論を先に述べますが、この命題は偽です。
数学では、仮定条件を満たすけれども、結論条件を満たさないものが 1 つでもあれば、その命題は偽(正しくない)とします。
この仮定条件を満たすけれども、結論条件を満たさないものを反例 (counter example)といいます。先ほどの命題は、すぐに反例が見つかります。そのため、偽ということになります。
具体例の命題の仮定条件は「x ≠ 0」で、結論条件は、「x ≧ 2」です。
1 という実数は、仮定条件を満たしますが、結論条件を満たしません。そのため、1 という実数が反例の一つです。
反例が一つでも存在するとき、その命題は偽となります。
変数の範囲は、命題の真偽に関わってくるので、大切です。仮定条件と結論条件が同じでも、前提となる変数の範囲を変えると、真偽が異なることもあります。
変数の範囲を変えると
【新しい命題】
x を 5 以上の実数とする。
このとき、x ≠ 0 ならば、x ≧ 2 である。
先ほどの具体例と、仮定条件、結論条件は同じです。
ちがいは、x の範囲です。「5 以上」の実数としました。
先ほどの命題よりも、x の範囲を小さくしました。
5 以上の実数は、どれも「x ≠ 0」という仮定条件を満たします。
さらに、「x ≧ 2」という結論条件を満たします。
このため、仮定条件を満たすものが、必ず結論条件を満たすため、この「新しい命題」は真です。
反例が存在するときに、変数に代入することができる値の範囲を狭くすると、命題が真になることがあります。
そのようにして、反例が 1 つも現れないように変数の範囲を設定すると、命題が真となるわけです。
R = {x | x は実数} という範囲内で考えていると、はじめの「具体例の命題」では、
1 ∈ R が反例となりました。
S = {x | x は 5 以上の実数} と、範囲を狭くすると、この S の中には、1 が含まれません。このようにして、変数に代入することができる値の範囲を狭くすることで、反例を除去するイメージです。
このように、命題の真偽では、集合を考えます。
数学2では、座標平面上の点たちを集めた集合を考え、命題の真偽を考えることもあります。
円の内部 – 領域 :平面上の点を変数に代入
【命題1】
x と y を実数とする。
このとき、xy > 0 ならば x > 0 かつ y < 0 である。
この命題だと、変数が x と y と二つあります。
{(x, y) | x, y は実数} という座標平面上の点全体が、前提となる変数の範囲となっています。
{(x, y) | x, y は実数} という座標平面上の点全体の部分集合のことを領域といいます。
{(x, y) | x, y は実数, xy > 0} という部分集合が、仮定条件を満たす座標平面上の点全体です。
{(x, y) | x, y は実数, x > 0, y < 0} が、結論条件を満たす座標平面上の点全体です。
仮定条件を満たす集合の要素で、結論条件を満たす集合の要素でないものが、反例となります。
【命題1】だと、点 (-1, -2) は、仮定条件を満たす集合の要素です。
しかし、点 (-1, -2) は、-1 が 0 より大きくないため、結論条件を満たす集合の元ではありません。そのため、反例となっています。
このように、座標平面上の点から成る集合について、論理を使って、命題の真偽を考えることができます。
それでは、いよいよ円と不等式を用いた命題を扱います。
円の内部と不等式
【命題2】
x2 + y2 = 4 という円の周および内部にある点を (x, y) とする。
このとき、5(x2 + y2) ≦ 45 である。
命題の前提となる変数の範囲が見えにくい状態になっています。そこで、集合を使って、明確に変数が動く範囲を確定させます。
{(x, y) | x, y は実数} という集合が、命題に使われている変数の動く範囲です。
{(x, y) | x, y は実数, x2 + y2 = 4} が、仮定条件の範囲となる集合です。
{(x, y) | x, y は実数, 5(x2 + y2) ≦ 45} という集合が、結論条件を満たす点たちの集合です。
ここで、不等式の性質から、
5(x2 + y2) ≦ 45 は、
x2 + y2 ≦ 9 と同値となっています。
集合に含まれているかどうかを判断するための条件を、同値な条件に書き換えても、同じ集合です。
つまり、
{(x, y) | x, y は実数, 5(x2 + y2) ≦ 45} は、
{(x, y) | x, y は実数, x2 + y2 ≦ 9} と同じ集合です。
そのため、
{(x, y) | x, y は実数, x2 + y2 ≦ 9} を結論条件を満たす点たちの集合と考えて良いということになります。
{(x, y) | x, y は実数, x2 + y2 = 9} だと、
原点 (0, 0) で半径 3 の円の周上の点全体です。
{(x, y) | x, y は実数, x2 + y2 < 9} だと、
原点 (0, 0) で半径 3 の円の内部の点全体です。
「原点 (0, 0) で半径 3 の円の周上の点全体」と「原点 (0, 0) で半径 3 の円の内部の点全体」の和集合が、結論条件を満たす点全体となっています。
「または」という和集合の意味は、「≦」という記号の意味からです。
「<」または「=」というのが、「≦」が表す意味です。
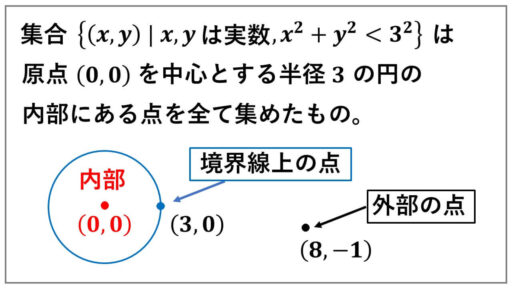
では、【命題2】を集合を用いた形で表し、真偽を考察します。
円の内部 – 領域 :集合と論理で考察
【命題3】
{(x, y) | x, y は実数} において、
{(x, y) | x, y は実数, x2 + y2 = 4} は、
{(x, y) | x, y は実数, x2 + y2 ≦ 9} の部分集合である。
ここまで、集合の範囲を明確にすると、真偽を考えやすいです。
「原点中心、半径 2 の円周上の点」であるならば、「原点中心、半径 3 の円周および、その内部の点」であるという内容です。
{(x, y) | x, y は実数, x2 + y2 = 4} の要素である点は、「原点中心、半径 3 の円周および、その内部の点」となっています。
よって、「命題2」は真です。
すなわち、仮定条件を満たすものが、必ず結論条件を満たすため、真ということです。
ちなみに、点 (1, 4) だと、
12+42 = 17 > 9 なので、結論条件の集合に含まれていない点ということになります。
反例となる点が存在するかどうかを、円の内部・周上・外部に分けて考察することが基本となります。
図形的考察によって、命題の真偽を考えるときに、論理と集合を正確に捉えると、ミスを減らせるかと思います。
使った図形的性質をまとめておきます。
円のまとめ
■ (x-a)2+(x-b)2 < r2
中心 (a, b), 半径 r の円の内部の点全体
■ (x-a)2+(x-b)2 = r2
中心 (a, b), 半径 r の円の周上の点全体
■ (x-a)2+(x-b)2 > r2
中心 (a, b), 半径 r の円の外部の点全体
座標で表されている点について考察しましたが、座標を使わない点や直線や三角形というものが、命題の変数として使われることもあります。
例えば、メネラウスの定理は、三角形と、その周上を通らない直線について考えます。
高校一年で学習する論理と集合を基礎とし、他の内容を合わせて考察することが多いです。そのため、論理や集合は数学の基礎となります。
最後に、円の中心と半径を計算する方法について述べておきます。円の内部や周上や外部ということを判断するために、円の方程式の形に式を計算して書き換えることが必要になるときがあります。
円の中心の座標と半径
x2-8x は、二乗の因数分解公式を使えそうで、少し形が異なるものになっています。
x2-8x+16 だと、二乗の因数分解が使え、
x2-8x+16 = (x2-4)2 となります。
そこで、
x2-8x = x2-8x+0
x2-8x+16-16 = (x-4)2-16 というように式を書き換えます。
この書き換えを使うことで、
x2-8x+y2-6y = 0 だと、
(x-4)2-16+(y-3)2-9 = 0 と書き換えます。
後は、-16-9 である-25 = -52 を右辺へ移項すると、
(x-4)2+(y-3)2 = 52 となります。
中心の座標が (4, 3) で半径が 5 の円の方程式が得られました。
この式の書き換えは、よく使うので、いつでも余裕で書き換えられるくらいに練習をしておくと良いかと思います。
また、文字を使っているときに、右辺は半径の二乗の形です。
円の半径は正の実数なので、文字を使っているときに、論理的な処理をするときもあるので注意です。
ここまで、数学2の内容を述べてきました。
数学3を選択した方用に、数3の微分を使って、円の接線の方程式を求めます。
数2の内容で円の接線を求めることもできますが、そこを数3の内容で求めることで、数2から数3への自然な連結を図ることができます。
円の内部 – 領域 :内部から周上の接点と接線
円の内部から円の周上へと視野を広げます。周上の 1 点のみが直線と円の共有点となっているときに、その直線を円の接線といい、その共有点を接点といいます。
まずは、中心 (0, 0)、半径 r の円の接線の方程式を合成関数の微分を使って求めます。
x2+y2 = r2 (r は定数) 上の点 (s, t) における接線の傾きを求めます。
t = 0 のときは、x = s が接線の方程式なので、y が 0 でないという状況で以下を議論します。
y2 = r2-x2 なので、
u = y2 = r2-x2 と置きます。
u は y の関数なので、u を y で微分すると、
du/dy = dy2/dy = 2y です。
また、u は x の関数でもあるので、
du/dx = d/dx(r2-x2) = -2x
また、合成関数の微分の公式を使うと、
du/dx = dy2/dy・dy/dx
よって、
-2x = 2y・dy/dx となり、
dy/dx = -x/y … ★
点 (s, t) における接線の傾きは、★について、x に s を代入し、y に t を代入すると、求まります。
-s/t が求める接線の傾きです。
この接線は、点 (s, t) を通るので、
y-t = -s/t×(x-s) が求める接線の方程式です。
右辺の括弧を外すと、
y-t = -sx/t+s2/t です。
両辺に t を掛けると、
ty-t2 = -sx+s2
よって、
sx+ty = s2+t2 … (1)
点 (s, t) は、x2+y2 = r2 上にあるので、
s2+t2 = r2 … (2)
(2) を (1) に代入すると、
sx+ty = r2 となります。
以上より、y ≠ 0 のとき、
円 x2+y2 = r2 上の点 (s, t) の接線の方程式は、
sx+ty = r2 です。
中心が(a,b)のとき
x2+y2 = r2 を x 軸方向へ a、y 軸方向へ b だけ平行移動をすると、
(x-a)2+(y-b)2 = r2 が中心 (a, b)、半径 r の円の方程式です。
この中心 (a, b)、半径 r の周上の点 (x1, y1) における接線の方程式を求めます。
y1 = 0 のときは、x = x1 が求める接線の方程式です。そのため、以下では y が 0 でないという設定で議論を進めます。
この円と接点と接線を x 軸方向へ -a, y 軸方向へ -b だけ平行移動します。
すると、
x2+y2 = r2 の接点 (x1-a, y1-b) における接線となります。
中心 (0, 0)、半径 r の円の接線の方程式の公式は、先ほど導出しているので、それを使います。
x2+y2 = r2 の接点 (x1-a, y1-b) における接線の方程式は、
(x1-a)x+(y1-b)y = r2 です。
この接線を x 軸方向に a、y 軸方向に b だけ平行移動すると、中心 (a, b)、半径 r の周上の点 (x1, y1) における接線の方程式となります。
y1 ≠ 0 のとき、
(x1-a)(x-a)+(y1-b)(y-b) = r2が中心 (a, b)、半径 r の周上の点 (x1, y1) における接線の方程式です。
図形と方程式について述べてきました。
絶対値に関連した不等式の証明についての記事も投稿しています。
また、高校一年の平面図形と論理を合わせた内容の
二つの円の位置関係という記事も投稿しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。