位数pqの群 ; 半直積 |群の構造を調べています

2023年1月11日

「 位数pqの群 」の構造（p と q は異なる素数）は、" 半直積 “か「内直積」になります。

整数についての論理から、可能性を絞り込み、どういった部分群が何個あるのかということを考えます。

群論の入門で学習する知識を利用しながら、位数 pq の群の構造を考察しています。

内直積や半直積については、このブログ記事で適宜、解説を加えています。

位数pqの群 ; 半直積 :起こり得る可能性

まずは、議論を組み立てていく上で、基本となる定理を述べておきます。

① 有限群 G の位数が素数 pⁿ (n は自然数)で割り切れるとき、位数 pⁿ の部分群が存在する。
② 有限群 G のシローp部分群の個数を n_p 個とすると、n_p は 群 G の位数の約数であり、

n_p = 1 + pk という形。ただし、k は 0 以上の非負整数。

これら①と②はシローの定理といわれるものたちです。

群 G の位数が pq (p と q は異なる素数) のときを考えるので、シローp部分群の個数 n_p とシローq部分群の個数 n_q について考えることになります。

定理の①から、n_p と n_q は、それぞれ 1 以上ですが、1 より大きいのかどうかということを考える必要があります。

論理で分けて考える

シローp部分群の個数 n_p について、
| G | = pq を n_p が割り切ることから、

n_p = 1 または p または q となります。

しかし、n_p = p だとすると、
1 + pk = p (k は非負整数) となり、

1 = p(1 – k) となってしまいます。

これは、p が 1 の約数ということを意味しているので、p が素数であることに反します。

そのため、n_p = 1 または q です。

シローq部分群の個数 n_q についても、同様の考察から、n_q = 1 または p となります。

これで、n_p と n_q について、4 通りの可能性があります。

高校で学習する整数についての考察の要領で、起こり得ない可能性を 1 つ除外することができます。

次に、n_p = q かつ n_q = p は起こらないということを背理法で示します。

背理法で除外

もし、n_p = q かつ n_q = p だとすると、
q = 1 + pk かつ p = 1 + qt

ただし、p, q は非負整数です。

さらに、p と q が素数なので、k も t も 0 ではないので、k と t は自然数ということが分かります。

辺々を掛け合わせると、
pq = (1 + qt)(1 + pk) > pq

pq > pq となり、これは矛盾です。

よって、背理法から n_p = q かつ n_q = p ではないということになります。

ゆえに、起こり得る可能性は、次の三つとなります。

n_p = 1 かつ n_q = 1 … (1)
n_p = q かつ n_q = 1 … (2)
n_p = 1 かつ n_q = p … (3)

(2) と (3) は、p と q の役割を逆にして同様の議論をするということから、(1) と (3) のときについて議論をすることにします。

結論は、(1) の場合、シローp部分群とシローq部分群の内直積になります。(3) のときは、シローp部分群とシローq部分群の半直積となります。

さらに考察を進めます。

まず群 G が、その部分群 H と N の内直積に分解するということについての必要十分条件を述べておきます。

位数pqの群 :内直積となるとき

【定理 1】

群 G の部分群を H と N とする。
G が 直積群 H × N と群として同型になることの必要十分条件は、次の①と②と③のすべてを満たすことである。
① H と N は G の正規部分群
② G = HN
③ H ∩ N = {e}
※ e は G の単位元

外直積と内直積より

リンク先の記事では、一般の n 個の部分群についての内直積を解説しています。

今回は、n = 2 の部分群についての内直積の議論をします。

| G | = pq で、n_p = 1 かつ n_q = 1 のとき、シローp部分群 N とシローq部分群 H は、どちらも正規部分群となっています。

理由は、任意の g ∈ G に対して、gNg^-1 の位数も p なので、gNg^-1 もシローp部分群です。

今、シローp部分群の個数 n_p が 1 なので、
gNg^-1 = N ということになります。

これは、N が G の正規部分群ということを示しています。

シローq部分群 H についても同様の議論から、G の正規部分群となります。

そのため、【定理 1】の条件①を満たしています。

条件②と③の確認

H ∩ N = {e} という条件③から確認します。

x ∈ H ∩ N がもし単位元 e と異なっていたと仮定します。

すると、x が H の元であることから、
ラグランジュの定理より、元 x の位数は素数 q となります。

※ 共役類という記事で、この定理の証明を解説しています。

しかし、x ∈ N でもあるので、ラグランジュの定理から元 x の位数は素数 p でもあります。

そのため、p = q となり、p と q が異なる素数であったことに矛盾します。

よって、x ∈ H ∩ N は単位元 e でなければなりません。

次に条件②の確認です。

HN = {xy | x ∈ H, y ∈ N} が G と一致することを示します。

シローp部分群 N の単位元と異なる元を b とすると、b の位数は p なので、N は b の一元で生成される巡回部分群ということになります。

シローq部分群 H の単位元と異なる元を a とすると、同じく H は a の一元で生成される巡回部分群です。

ここで、ab ∈ HN の位数を考えます。ab の位数を s とすると、s は pq の約数です。
そのため、s = 1, p, q, pq のどれかということになります。

s = 1 とすると、ab = e より、a = b^-1 = b^p-1 ∈ N となり、a の元の位数が q だったことに反します。

そこで、s ≧ 2 とします。

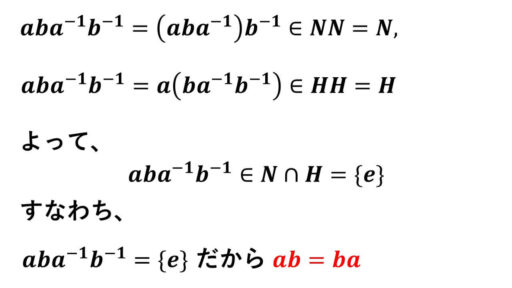
これで、N と H の生成元どおしが可換であることが分かりました。
※ 交換子については、リンク先の記事で解説をしています。

ab の位数は s だったので、
e = (ab)^sp = a^spb^sp = a^spe

つまり、e = a^sp

a の位数は q なので、sp は q で割り切れます。

そして、q と p は異なる素数で最大公約数が 1 ということから、q が s の約数ということになります。

同様に、e = b^sq となり、b の位数が p なので、p が s の約数ということになります。

そのため、pq が s の約数ということになり、

pq ≦ s です。

さらに、ab は G の元で、G の位数が pq であることから、ab の位数 s は pq 以下であることと合わせると、pq = s

よって、ab の位数は pq です。
　
条件①は示せているので、N が G の正規部分群であることから、HN は G の部分群なので、ab のベキ乗も HN の元です。

ゆえに、G = ＜ab＞ = HN

これで、条件③も満たすことが示せました。
　
これで、【定理 1】から、G が H と N の直積と同型であるということになります。

【定理 1】の同型から、G の任意の元 g は、
ある x ∈ H = ＜b＞と y ∈ N = ＜a＞を用いて、g = xy と一意的に表されるということになります。

この (1) 「n_p = 1 かつ n_q = 1」は、有限群 G の位数が、位数 15 や位数 35 のときが具体例となります。

位数 35 だと、p = 5, q = 7 で、シロー5群とシロー7群の直積と同型ということになります。

今度は、「n_p = 1 かつ n_q = p」という (3) のときについて、半直積となることを説明します。

位数pqの群 :半直積となるとき

シローp部分群 N の個数 n_p が 1 で、シローq部分群の個数 n_q が p のときも、先ほどと同様に、H ∩ N = {e} となっています。

n_p = 1 なので、N が G の正規部分群であることから、HN が G の部分群になっているので、

HN = G も先ほどと同じ議論で成立しています。

HN = NH なので、NH = G となっています。

しかし、n_q = p ≠ 1 なので、シローq部分群は G の正規部分群ではありません。

そのため、HN = G は、H × G と同型ではありません。

今回は、NH が 半直積と同型になっています。

半直積 – 定義

群 N について、N から N への群自己同型写像全体を Aut N とし、群 H から Aut H への群準同型写像を f とします。

このとき、直積集合 N × H に次のように積を定義してできる群のことを N と H の半直積といいます。

n₁, n₂ ∈ N, h₁, h₂ ∈ H について、

(n₁, h₁)(n₂, h₂)
= (n₁f(h₁)(n₂), h₁h₂) を、N × H の積とします。

この N × H の積について、単位元の存在、逆元の存在、結合律が成立して群となります。

第 2 成分については、第 2 成分どおしで H における積をとるのですが、第 1 成分の方が少しややこしい定義なので、補足をしておきます。

f(h₁) ∈ Aut N なので、f(h₁) は N から N への群同型写像です。

よって、f(n1) によって、n₂ が移された像は、f(h₁)(n₂) ∈ N です。

そのため、n₁ とで N における積を計算したものが、n₁f(h₁)(n₂) ∈ N となっています。

この半直積は、一つの群の部分群とは限らない N と H について定義されています。

さらに、条件が加わって、N が群 G の正規部分群で、H が G の部分群という状況だとします。

このときは、f として、内部自己同型写像を対応させる写像を考えることで、半直積と話がつながります。

内部自己同型写像

群 G の元 g について、σ_g を次の G から G への写像とします。
x ∈ G に対して、σ_g(x) = gxg^-1

この σ_g を G の内部自己同型写像といいます。

全単射群準同型写像より、σ_g ∈ Aut G

G の各元 g に応じて、一つ内部自己同型写像 σ_g が定義できるので、
g ∈ G に対して、Ψ(g) = σ_g ∈ Aut G と写像 Ψ を定義できます。

この Ψ は、G から Aut G への群準同型写像となっています。

今、H が G の部分群なので、h ∈ H について、Ψ(h) は Aut G の元です。

さらに、N が G の正規部分群なので、
Ψ(h)(N) = hNh^-1 = N です。

したがって、Ψ(h)|_N という Ψ(h) の N への制限写像は、N の群自己同型写像となります。

つまり、h ∈ H に対して、
f(h) = Ψ(h)|_N

と写像 f を定義すると、f は H から Aut N への準同型写像となります。

実際、n ∈ N に対して、
Ψ(h)|_N(n) = hnh^-1 ∈ hNh^-1 = N

半直積との群同型

n₁, n₂ ∈ N , h₁, h₂ ∈ H とし、
NH = {yx | y ∈ N, x ∈ H} = G における積を計算します。

(n₁h₁)(n₂h₂)
= n₁(h₁n₂h₁^-1)h₁h₂
= n₁Ψ(h₁)|_N(n₂)h₁h₂
= n₁f(h₁)(n₂)h₁h₂

よって、(n₁h₁)(n₂h₂) ∈ NH は、直積 N × H に半直積の積を定義した

(n₁f(h₁)(n₂), h₁h₂) に対応します。

π : NH → N × H を
π(nh) = (n, h) と定義すると、明らかに全射です。

N と H の単位元は G の e なので、
ker π = {ee} = {e} だから単射です。

そして、
π((n₁h₁)(n₂h₂))
= π(n₁f(h₁)(n₂)h₁h₂)
= (n₁f(h₁)(n₂), h₁h₂)
= (n₁, h₁)(n₂, h₂) = π(n₁h₁)π(n₂h₂)

なので、群準同型写像となっています。

これで、半直積と群同型になっていることが確認できました。

この片方のシロー部分群が 2 つ以上ある具体例は、3 次対称群 S₃ です。
| S₃ | = 6 = 3 × 2 なので、シロー3部分群の個数が 1 です。

一方、シロー2群の個数は 3 です。

シロー2群の方が正規部分群ではありません。

【関連する記事】

群の公理という記事で、群についての基礎的な内容を解説しています。

自己同型写像という記事では、群の自己同型写像について述べています。

これで、今回のブログ記事を終了します。

読んで頂き、ありがとうございました。