直積集合 | 添数集合と無限個の空でない集合たちでの定義へ
" 直積集合 “について、無限個の空でない集合たちの直積の定義を解説しています。
まず2個の集合の直積から始め、添数集合を利用した直積集合の定義へと議論を進めています。
また、二つの集合の元(要素)で作った順序対を集めてできる直積集合を用いて、二項演算が定義されます。
中学一年のときから使っている xy-座標平面は実数全体から成る集合どおしで直積集合を作ったものです。
確率の単元だと、二つのサイコロを投げるときに、集合たちで直積集合を考えて、事象が作られていたりします。
結構、身近に使われている直積集合です。
記事の終盤で添数集合を用いた直積の定義を説明する流れになっています。
直積集合 :順序対を考える
【直積集合の定義】
集合 A, B に対して、
A × B = { (a, b) | a ∈ A, b ∈ B } という順序対をすべて集めた集合を A と B の直積集合という。
a ∈ A, b ∈ B のとき、両者を並べる順序まで考慮した順序対というものを考えます。
(a, b) が順序対で、a の値のことを第1成分、b の値のことを第2成分といいます。
中学数学で xy 座標平面上の点を表すものとして、
(2, 3) といったものを学習しています。
実数でなくても、(a, b) というように集合の元を順序つきで並べることで、順序対が定義できます。
a , x ∈ A と b, y ∈ B について、
二つの順序対 (a, b) と (x, y) が等しいということの定義があります。
(a, b) = (x, y) の定義は、
a と x が A の元として等しく、
かつ b と y が B の元として等しいということです。
そして、集合 A と集合 B が与えられたときに、A と B の直積集合が定義されます。
{(a, b) | a ∈ A, b ∈ B} という集合を
A と B の直積集合といい
A × B と表します。
ちなみに、集合 A と集合 B が等しいときにも直積集合が定義されます。
A = B のときに、A × A のことを A2 と表すときもあります。
実数全体から成る集合を R と表すことにすると、
R × R 、つまり、R2 が xy 座標平面全体の点を表しています。
R × R = R2 = {(x, y) | x, y ∈ R} が、座標平面上の点全体を表す集合です。
一般に、集合 A を n 個分で直積をとった集合を An と表します。
(a1, a2, ・・・, an) と、A の元が n 個並んだ順序対をすべて集めた集合となります。
実数全体 R を 3 個で直積集合を作ると空間座標です。
R × R × R = R3 ∋ (x, y, z) が、空間内の点を表します。
順序対からの二項演算
空集合ではない集合 S が与えられたときに、
S × S から S への写像(関数)のことを S 上の二項演算といいます。
f : S × S → S について、
(a, b) ∈ S × S に対応する値 f(a, b) ∈ S のことを、
f を使わずに ab と積の形で書くことにします。
f の他にも二項演算が定義されているというときもあります。
体だと、乗法以外に加法という二項演算も定義されています。
加法については、「+」の記号を用いて表すことにします。
体の公理(定義)について、まとめておきます。
空集合ではない集合 K に、二種類の二項演算が定義されていることが前提となります。
直積集合 :体の公理(定義)
K × K → K
(a, b) → a + b
(a, b) → a・b
二種類の二項演算の計算結果を「+」と「・」で表すことにします。
「+」の方が、以下の加法の条件を満たすものということになります。
加法となる「+」の二項演算について、交換法則と結合法則が成立することが条件となります。
また、乗法「・」についても、交換法則と結合法則が成立することが条件となります。
そして、加法と乗法という二種類の二項演算をつなぐ分配法則も成立することが条件となります。
以下に書く a, b, c ∈ K は、体の任意の元を表しています。
【加法の交換法則】
a+b = b+a
【加法の結合法則】
(a+b)+c = a+(b+c)
【乗法の交換法則】
ab = ba
【乗法の結合法則】
(ab)c = a(bc)
例えば、高校数学で学習する複素数全体の加法と乗法をイメージして頂くと、確かに、これらの条件を満たしています。
そして、加法と乗法を結び付けているのが分配法則になります。
【分配法則】
a, b, c ∈ K に対して、
a (b + c) = ab + ac,
(a + b)c = ac + bc
分配法則について、上が左分配法則、下が右分配法則です。
通常は体といったときに、左右の分配法則が成立することを条件とします。
※ 一般の分配法則は、加法についての一般結合法則を利用して、帰納法を使って証明されます。
単位元・逆元
単位元と逆元は、加法についてのものと、乗法についてのものがあります。
【加法についての単位元】
加法について 0K ∈ K が次を満たすとき、0K を加法についての単位元といいます。
a ∈ K に対して、a + 0K = a
すでに、加法について交換法則が成立することが述べられているので、0K + a = a ということにもなります。
【乗法についての単位元】
乗法について 1K ∈ K が次を満たすとき、1K を乗法についての単位元といいます。
a ∈ K に対して、a・1K = a
乗法の交換法則から、1K・a = a も成立していることになります。
【加法についての逆元】
a ∈ K に対して、-a ∈ K が存在して、
a + (-a) = 0K
つまり、どの K の元についても、加法を計算したときに、加法についての単位元 0K が計算結果となる元が存在するということです。
【乗法についての逆元】
x ∈ K を 0K ではない任意の元とする。
この x に対して、x-1 ∈ K が存在して、
x・x-1 = 1K
これで、体の公理(定義)となる条件をすべて書きました。
ただ、加法についての単位元 0K を、乗法の逆元の条件から除いていることに注意です。
これは、もし、加法についての単位元が、乗法についての逆元をもったとすると、
体 K が 0K のみの 1 点集合になってしまうからです。
仮に、0K が乗法についての逆元 (0K)-1 をもったとすると、任意の a ∈ K に対して、
a = a・1K = a・{0K・(0K)-1}
= (a・0K)・ (0K)-1 = 0K・(0K)-1 = 1K
このように、体K のどの元 a も 1K と等しくなってしまいます。
そうすると、特に、任意にとった a ∈ K として、加法についての 0K を考えると、
0K = 1K となります。
加法についての単位元 0K は、体 K のどの元と乗法を計算しても、計算結果は必ず 0K になります。
このことは、加法についての単位元が乗法についての逆元をもつかどうかに関わらずに成立します。
任意の b ∈ K に対して、
b・0K = b・(0K + 0K)
= b・0K + b・0K
b・0K = b・0K + b・0K の両辺に、
-(b・0K) を加えると、0K = b・0K
「0K は体 K のどの元と乗法を計算しても計算結果は必ず 0K になる」ということと、
先ほどの 0K = 1K となることを合わせます。
すると、体 K のどんな元 b も、0K に一致するということになってしまいます。
b ∈ K に対して、
b = b・1K = b・0K= 0K となってしまいます。
ですので、 0K = 1K とならないために、体の乗法についての逆元の存在について、加法についての単位元 0K のことを除いているわけです。
小学校の算数から、ゼロで割ることはできない。
もしくは、分数の分母にゼロを書いてはいけないということを習います。
ゼロで割って良いとしてしまうと、ゼロについて乗法の逆元の存在を認めたことになってしまいます。
そうすると、実数体がゼロのみの集合となってしまうからです。
最後に、ベクトル空間の直積について述べます。
線形代数の直積
このページの前半で、R × R が R 上の線形代数(ベクトル空間)であることを述べました。
この内容を一般化して、同じ体からのスカラー倍をされている 2 つのベクトル空間から新しいベクトル空間を定義する方法を説明します。
V と W を体 K 上のベクトル空間とします。このとき、次のようにして、直積集合 V × W を体 K 上のベクトル空間とすることができます。
【V × W の和】
(v, w), (x, y) ∈ V × W に対して、
(v, w) + (x, y) = (v + x, w + y) と成分ごとに和を定義します。
同じ加法の記号を使っていますが、
v + x は V における加法で、
w + y は W における加法です。
既に定義されているベクトル空間 V と W における加法を利用して、直積集合における加法を定義しています。
【V × W へのスカラー倍】
k ∈ K からの (v, w) ∈ V × W へのスカラー倍を、
k(v, w) = (kv, kw) と定義します。
※ 既に V と W において定義されているスカラー倍を使って定義しています。
これで、直積集合 V × W について和と体 K からのスカラーが定義されました。
この和とスカラー倍の定義について、ベクトル空間の公理を満たします。
そのため、V × W は単なる集合ではなく、体 K 上のベクトル空間という代数学的な構造が確立されています。
このようにして、体 K 上の二つのベクトル空間 V と W から直積集合 V × W を体 K 上のベクトルにする方法を外部直和といいます。
ちなみに、名前のごとく内部直和というものも定義されています。
内部直和は、体 K 上のベクトル空間 V の部分空間 V1 と V2 から、新しい V の部分空間を定義する方法です。
内部直和についての詳細は、直和空間という記事で説明をしています。
ここまで有限個の集合の直積集合と二項演算について述べました。
無限個の集合で直積集合を定義するときには、添数集合を使います。
無限個の直積も添数集合を用いて
添数集合 Λ の元 λ に対して、1つの集合を対応させることがあります。
(Aλ)λ∈Λ を始集合 Λ からの対応を表す写像とします。
∪λAλ が終集合です。
【簡単な例】
Λ = {1, 2, 3} とします。
1 に対応する集合が A1 = {5}、
2 に対応する集合が A2 = {6, 7}、
3 に対応する集合 A3 が空集合 Φ とします。
(Aλ)λ∈Λ によって、対応する集合たちの集まりは、
{A1, A2, A3} = {{5}, {6, 7}, Φ}
各 λ∈Λ に対して、Aλ を対応させている写像 (Aλ)λ∈Λ が与えれれると、上のように対応する集合たちをすべて集めたものが認識できます。
そのため、Λ が無限集合のときに、無限個の集合たちの直積集合を定義するというわけです。
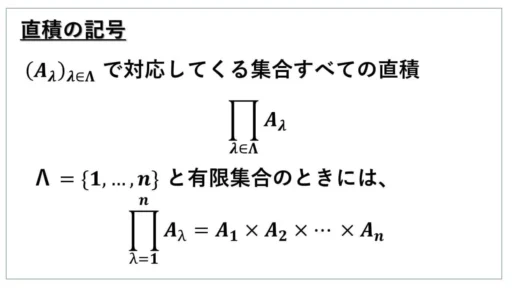
一般個数の直積の定義
先ほどの例では、Λ が有限個のときを述べましたが、Λ が無限集合というときもあります。
ここで、(Aλ)λ∈Λ による集合たちの集まりに含まれている集合について、それらすべての直積を表す記号を説明します。
また、直積の元とは何かということについても説明します。
各 λ ∈ Λ に対して Aλ は空集合ではないということを前提として議論を述べます。
一般の直積の元の定義は、認識をしっかりとしておく必要があります。
<直積の元>
直積の元は、次の条件(*)を満たす添数集合 Λ を定義域とする写像 aです。
条件 (*) : 各 λ ∈ Λ に対し a(λ) ∈ Aλ
※ a(λ) のことを aλ と表すときもあります。
この条件 (*) を満たす写像たちをすべて集めた集合が、
Λ によって添数付けられた集合たちの直積集合です。
(Aλ)λ∈Λ は、各 λ ∈ Λ に対して Aλ を対応させている写像でした。
直積集合 Πλ Aλ の元である写像と間違えないように注意です。
この直積についての定義を押さえると、多項式環の不定元といった内容を理解することへとつながります。
Λ が有限集合のときには、今まで使ってきた直積の認識からすると違和感があるかと思います。
それは、有限個の直積のときには、書き換えがあるからです。
有限個の直積については、次の書き換えた方を通常は使っていました。
有限個のときの書き換え
Λ = {1, 2} という二個の直積のときの書き換えです。
条件 (*) を満たす写像 a が与えられたときに、
a1 ∈ A1, a2 ∈ A2 となっているため、
(a1, a2) という組が形成できます。
( a(λ) のことを aλ と表す表し方をしました。)
逆に、(s, t) という組で、
s ∈ A1, t ∈ A2 となっているものが与えられたとします。
Λ を定義域とする条件 (*) を満たす写像 a を、
a(1) = a1 = s, a(2) = a2 = t と定義できます。
以上より、
「条件 (*) を満たす Λ を定義域とする写像が与えられること」の必要十分条件が、
「(s, t) という組で、s ∈ A1, t ∈ A2 となっているものが与えられること」となります。
このため、写像を使った一般の直積の元の定義を、見慣れた組を使った定義に書き換えることができます。
今、二個の直積についての書き換えを述べましたが、一般に A1 から An までの n 個の直積について組を用いた書き換えが可能です。
(a1, a2, … , an) という n 個のそれぞれの集合の元から成る組で表すことができます。
一般的に数学の議論で、添数集合 Λ が有限集合のとき、有限個の直積の元は組を使って表されることが多いです。
しかし、添数集合 Λ は無限個のとき、自然数全体のように大小関係の順番が定義されていないというときさえあります。
添数集合 Λ が無限集合のときには、無限個の元たちの組というものを無理に表そうとはしないで、条件 (*) を満たす写像の方で表されます。
<注意点>
条件 (*) で、各 λ ∈ Λ に対して、a(λ) ∈ Aλ とありました。
a(λ) ∈ Aλ ということについて、満たさない例も書いておきます。
Λ = {1, 2} で、A1 と A2 はどちらも実数全体 R としておきます。
Λ を定義域とする次の写像が直積 R × R の元かどうかを判断してみます。
f(1) = 5, 「f(2) を 3 行 3 列の実数を成分とする単位行列」とします。
この f は確かに Λ を定義域としています。
そして、f(1) = 5 ∈ R = A1 となっています。
しかし、f(2) は実数を成分とする 3 行 3 列の行列なので実数ではないため、R には含まれません。
そのため、f(2) は A2 = R に含まれていません。
したがって、条件 (*) を満たしていないので、この f は直積 R × R の元ではないということになります。
添数集合 Λ のそれぞれの元 に対して、なんでもかんでも値を対応させれば良いというわけではないということです。
値を対応させたとしても、a(λ) が Aλ に含まれないときもあるということを知っておくと、選択公理についての実感がもてるかと思います。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。